Giải bài 5 tr 146 sách GK Toán GT lớp 12
Cho hàm số y = x4 + ax2 + b
a) Tính a, b để hàm số có cực trị bẳng \(\frac{3}{2}\) khi x = 1.
b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho khi \(a=-\frac{1}{2}\), b= 1.
c) Viết phương trình tiếp tuyến của (C) tại các điểm có tung độ bằng 1.
Hướng dẫn giải chi tiết bài 5
Phương pháp:
Câu a: Sử dụng điều kiện cần để hàm số có cực trị:
Hàm số\(f(x)\) đạt cực trị tại \(x_0\), có đạo hàm tại \(x_0\) thì \(f'(x_0)=0\).
Câu b: Áp dụng các bước khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn trùng phương.
Câu c: Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại tiếp điểm M(x0,y0) thuộc đồ thị hàm số đã học ở chương trình lớp 11 có dạng:
\(y-y_0=f'(x_0)(x-x_0)\)
Lời giải:
Câu a:
Ta có \(y'=4x^3+2ax\)
Hàm số có cực trị bằng \(\frac{3}{2}\) khi x = 1
\(\Leftrightarrow \left\{\begin{matrix} y'(1)=0\\ y(1)=\frac{3}{2} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4+2a=0\\ a+b=\frac{1}{2} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=-2\\ b=\frac{5}{2} \end{matrix}\right.\)
Câu b:
Khi \(a=-\frac{1}{2}, b=1\) ta có \(y=x^4-\frac{1}{2}x^2+1\)
Tập xác định: D = R.
Giới hạn: \(\lim_{x\rightarrow \pm \infty }y=+\infty\)
Sự biến thiên:
\(y'=4x^3-x=x(4x^2-1)\)
\(y'=0\Leftrightarrow \Bigg \lbrack \begin{matrix} x=0 \ \ (y=1)\\ \\ x=\pm \frac{1}{2} \ \ (y=\frac{15}{16}) \end{matrix}\)
Bảng biến thiên:
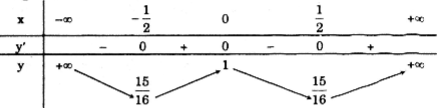
Hàm số đồng biến trên các khoảng \(\left ( -\frac{1}{2};0 \right )\) và \(\left( {\frac{1}{2}; + \infty } \right)\); nghịch biến trên các khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { 0; \frac{1}{2}} \right).\)
Cực trị:
Hàm số đạt cực đại tại x=0, giá trị cực đại ycđ=1; Đạt cực tiểu tại \(x=\frac{1}{2}\) và \(x=-\frac{1}{2}\), giá trị cực tiểu \(y_{ct}=\frac{15}{16}.\)
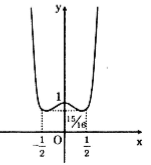
Đồ thị hàm số:
Đồ thị hàm số nhận trục Oy làm trục đối xứng.
Đồ thị hàm số đi qua các điểm \(\left ( 1;\frac{3}{2} \right )\) và \(\left ( -1;\frac{3}{2} \right ).\)
Đồ thị:
Câu c:
Ta có:
\(y=1\Leftrightarrow x^4-\frac{1}{2}x^2+1=1\Leftrightarrow x^4-\frac{1}{2}x^2=0\)
\(\Leftrightarrow x^2(x^2-\frac{1}{2})=0\Leftrightarrow \Bigg \lbrack \begin{matrix} x=0\\ \\ x=\pm \frac{1}{\sqrt{2}} \end{matrix}\)
Ta có ba tiếp điểm \(A(0;1), B(\frac{1}{\sqrt{2}};1), C(-\frac{1}{\sqrt{2}};1)\)
- Tại A(0;1) ta có y'(0) = 0
Phương trình tiếp tuyến tại A: y - 1 = 0 ⇔ y = 1.
- Tại \(B(\frac{1}{\sqrt{2}};1)\) ta có \(y'(\frac{1}{\sqrt{2}})=\frac{1}{\sqrt{2}}\)
Phương trình tiếp tuyến tại B: \(y-1=\frac{1}{\sqrt{2}}(x-\frac{1}{\sqrt{2}})\Leftrightarrow y= \frac{1}{\sqrt{2}}x+\frac{1}{2}\).
- Tại \(C(-\frac{1}{\sqrt{2}};1)\) ta có \(y'(-\frac{1}{\sqrt{2}})=-\frac{1}{\sqrt{2}}\)
Phương trình tiếp tuyến tại C: \(y-1=-\frac{1}{\sqrt{2}}(x+\frac{1}{\sqrt{2}})\Leftrightarrow y=- \frac{1}{\sqrt{2}}x+\frac{1}{2}\).
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3 trang 146 SGK Giải tích 12
Bài tập 4 trang 146 SGK Giải tích 12
Bài tập 6 trang 146 SGK Giải tích 12
Bài tập 7 trang 146 SGK Giải tích 12
Bài tập 8 trang 147 SGK Giải tích 12
Bài tập 9 trang 147 SGK Giải tích 12
Bài tập 10 trang 147 SGK Giải tích 12
Bài tập 11 trang 147 SGK Giải tích 12
Bài tập 12 trang 147 SGK Giải tích 12
Bài tập 13 trang 148 SGK Giải tích 12
Bài tập 14 trang 148 SGK Giải tích 12
Bài tập 15 trang 148 SGK Giải tích 12
Bài tập 16 trang 148 SGK Giải tích 12
Bài tập 1 trang 211 SGK Toán 12 NC
Bài tập 2 trang 211 SGK Toán 12 NC
Bài tập 3 trang 211 SGK Toán 12 NC
Bài tập 4 trang 212 SGK Toán 12 NC
Bài tập 5 trang 212 SGK Toán 12 NC
Bài tập 6 trang 212 SGK Toán 12 NC
Bài tập 7 trang 212 SGK Toán 12 NC
Bài tập 8 trang 212 SGK Toán 12 NC
Bài tập 9 trang 212 SGK Toán 12 NC
Bài tập 11 trang 213 SGK Toán 12 NC
Bài tập 12 trang 213 SGK Toán 12 NC
Bài tập 13 trang 213 SGK Toán 12 NC
Bài tập 14 trang 213 SGK Toán 12 NC
Bài tập 15 trang 213 SGK Toán 12 NC
Bài tập 16 trang 213 SGK Toán 12 NC
Bài tập 17 trang 213 SGK Toán 12 NC
Bài tập 18 trang 214 SGK Toán 12 NC
Bài tập 19 trang 214 SGK Toán 12 NC
Bài tập 20 trang 214 SGK Toán 12 NC
Bài tập 21 trang 214 SGK Toán 12 NC
Bài tập 22 trang 214 SGK Toán 12 NC
Bài tập 23 trang 214 SGK Toán 12 NC
Bài tập 24 trang 214 SGK Toán 12 NC
Bài tập 25 trang 215 SGK Toán 12 NC
Bài tập 26 trang 214 SGK Toán 12 NC
Bài tập 27 trang 215 SGK Toán 12 NC
Bài tập 28 trang 215 SGK Toán 12 NC
Bài tập 29 trang 215 SGK Toán 12 NC
Bài tập 30 trang 215 SGK Toán 12 NC
Bài tập 31 trang 216 SGK Toán 12 NC
Bài tập 32 trang 216 SGK Toán 12 NC
Bài tập 33 trang 216 SGK Toán 12 NC
Bài tập 34 trang 216 SGK Toán 12 NC
Bài tập 35 trang 216 SGK Toán 12 NC
Bài tập 36 trang 217 SGK Toán 12 NC
Bài tập 37 trang 217 SGK Toán 12 NC
Bài tập 38 trang 217 SGK Toán 12 NC
Bài tập 1 trang 216 SBT Toán 12
Bài tập 2 trang 216 SBT Toán 12
Bài tập 3 trang 216 SBT Toán 12
Bài tập 4 trang 216 SBT Toán 12
Bài tập 5 trang 216 SBT Toán 12
Bài tập 6 trang 216 SBT Toán 12
Bài tập 7 trang 216 SBT Toán 12
Bài tập 8 trang 217 SBT Toán 12
Bài tập 9 trang 217 SBT Toán 12
Bài tập 10 trang 217 SBT Toán 12
Bài tập 11 trang 217 SBT Toán 12
Bài tập 12 trang 218 SBT Toán 12
Bài tập 13 trang 218 SBT Toán 12
Bài tập 14 trang 218 SBT Toán 12
Bài tập 15 trang 218 SBT Toán 12
Bài tập 16 trang 218 SBT Toán 12
Bài tập 17 trang 218 SBT Toán 12
Bài tập 18 trang 219 SBT Toán 12
Bài tập 19 trang 219 SBT Toán 12
Bài tập 20 trang 219 SBT Toán 12
Bài tập 21 trang 219 SBT Toán 12
Bài tập 22 trang 219 SBT Toán 12
Bài tập 23 trang 220 SBT Toán 12
Bài tập 24 trang 220 SBT Toán 12
Bài tập 25 trang 220 SBT Toán 12
-


Cho biết hàm số \(y = f(x)\) có bảng biến thiên trên đoạn \(\left[ { - 1;5} \right]\) như hình vẽ. Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(f\left( {3\sin x + 2} \right) = m\) có đúng 3 nghiệm phân biệt trên khoảng \(\left( { - \dfrac{\pi }{2};\pi } \right)\) ?
bởi Lê Minh Trí
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = f(x)\) có đạo hàm liên tục trên \(\mathbb{R},\) hàm số \(y = f'(x)\) có đồ thị như hình vẽ. Cho biết số điểm cực trị của hàm số \(y = f(1 - x)\)
bởi Lan Ha
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Trong các mặt cầu tiếp xúc với hai đường thẳng sau \({\Delta _1}:\left\{ \begin{array}{l}x = t\\y = 2 - t\\z = - 4 + 2t\end{array} \right.,\;{\Delta _2}:\left\{ \begin{array}{l}x = - 8 + 2t\\y = 6 + t\\z = 10 - t\end{array} \right.;\) phương trình mặt cầu có bán kính nhỏ nhất là
bởi Nguyễn Phương Khanh
 28/04/2022
Theo dõi (0) 1 Trả lời
28/04/2022
Theo dõi (0) 1 Trả lời -


Cho biết \(\int\limits_{ - 1}^4 {x\ln \left( {x + 2} \right){\rm{d}}x} = a\ln 6 + \dfrac{5}{b}\) với \(a,b\) là các số nguyên dương. Tính giá trị \(2a + 3b\)
bởi Nguyễn Phương Khanh
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho hàm số sau \(y = f(x)\) có bảng biến thiên như hình bên. Số nghiệm của phương trình \(3f(x) - 2 = 0\)
bởi Khanh Đơn
 28/04/2022
Theo dõi (0) 1 Trả lời
28/04/2022
Theo dõi (0) 1 Trả lời -


Hãy tính tích các nghiệm thực của phương trình \(\log _2^2x + \sqrt {3 - {{\log }_2}x} = 3\)
bởi Trần Hoàng Mai
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = f\left( x \right)\) liên tục trên \({\rm{[}}1;2{\rm{]}}.\) Quay hình phẳng \(\left( H \right) = \left\{ {y = f(x),y = 0,x = 1,x = 2} \right\}\) xung quanh trục \(Ox\) được khối tròn xoay có thể tích
bởi thanh duy
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Tìm gố giao điểm của đồ thị hàm số \(y = {x^3} - 3x + 1\) và đường thẳng \(y = 3\)
bởi Minh Tú
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Kí hiệu \({z_1},{z_2}\) là hai nghiệm phức của phương trình \({{\rm{z}}^2} + z + {2019^{2018}} = 0.\) Tính diá trị \(\left| {{z_1}} \right| + \left| {{z_2}} \right|\)
bởi bach hao
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Ta gọi \({z_1}\) và \({z_2}\) là hai nghiệm phức của phương trình \({z^2} + 2z + 10 = 0\). Tính giá trị biểu thức \(\left| {{z_1}} \right| + \left| {{z_2}} \right|\)
bởi Lê Bảo An
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Lớp 12A có 35 học sinh, trong đó có 3 học sinh cùng tên là Trang, 2 học sinh cùng tên là Huy. Xếp ngẫu nhiên 35 học sinh thành một hàng dọ. Tính xác suất để 3 học sinh tên Trang đứng cạnh nhau và 2 học sinh tên Huy đứng cạnh nhau.
bởi Dell dell
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Cho biết \(\int\limits_1^2 {f\left( x \right)} {\rm{d}}x = 2\) và \(\int\limits_1^2 {\left[ {2f\left( x \right) - g\left( x \right)} \right]} {\rm{d}}x = 3;\) giá trị \(\int\limits_1^2 {g\left( x \right)} {\rm{d}}x\) bằng
bởi thuy tien
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Hãy tính đạo hàm của hàm số \(f\left( x \right) = {\log _2}\left( {3{x^2} + 2} \right)\)
bởi Huy Hạnh
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x) = x{(x + 1)^2}{(x - 3)^3},\forall x \in \mathbb{R}\). Tìm số điểm cực trị của hàm số
bởi can tu
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Giả sử có \(a,b\) là các số thực sao cho \({x^3} + {y^3} = a{.10^{3z}} + b{.10^{2z}}\) đúng với mọi các số thực dương \(x,y,z\) thoả mãn sau \(\log \left( {x + y} \right) = z\) và \(\log \left( {{x^2} + {y^2}} \right) = z + 1.\) Giá trị của \(a + b\) bằng
bởi Hy Vũ
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời -


Tìm nghiệm của phương trình \({2^x} = 16\)
bởi Minh Thắng
 29/04/2022
Theo dõi (0) 1 Trả lời
29/04/2022
Theo dõi (0) 1 Trả lời


.JPG)
.JPG)
.JPG)
