Bài tập 3 trang 211 SGK Toán 12 NC
Gọi (C) là đồ thị của hàm số y = ln x và (D) là một tiếp tuyến bất kỳ của (C).
Chứng mình rằng trên khoảng (0, +∞); (C) nằm ở phía dưới đường thẳng (D).
Hướng dẫn giải chi tiết
Giả sử M(x0, lnx0) ∈ (C) (x0 > 0 )
Ta có: \(y' = \frac{1}{x}\)
Tiếp tuyến của (C) tại M có phương trình là:
\(y = \frac{1}{{{x_0}}}(x - {x_0}) + \ln {x_0}\)
Vậy với mọi x ∈ (0,+∞), ta cần chứng minh:
\(\begin{array}{l}
\frac{1}{{{x_0}}}(x - {x_0}) + \ln {x_0} \ge \ln x\\
\Leftrightarrow \frac{x}{{{x_0}}} - 1 - \ln \frac{x}{{{x_0}}} \ge 0
\end{array}\)
Đặt \(t = \frac{x}{{{x_0}}} > 0\)
Xét hàm số \(g(t) = t-\ln t\) với t > 0
\(\begin{array}{l}
g' = 1 - \frac{1}{t} = \frac{{t - 1}}{t}\\
g' = 0 \Leftrightarrow y = t = 1
\end{array}\)
Bảng biến thiên
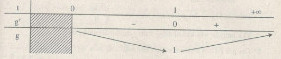
Từ bảng biến thiên ta có \(g(t) \ge 1\) với mọi \(t \in (0, + \infty )\)
\(\begin{array}{l}
\Rightarrow t - \ln t - 1 \ge 0\\
\Rightarrow \frac{x}{{{x_0}}} - 1 - \ln \frac{x}{{{x_0}}} \ge 0,\forall x > 0
\end{array}\)
Vậy trên \((0; + \infty )\) (C) nằm phía dưới đường thẳng (D).
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 1 trang 211 SGK Toán 12 NC
Bài tập 2 trang 211 SGK Toán 12 NC
Bài tập 4 trang 212 SGK Toán 12 NC
Bài tập 5 trang 212 SGK Toán 12 NC
Bài tập 6 trang 212 SGK Toán 12 NC
Bài tập 7 trang 212 SGK Toán 12 NC
Bài tập 8 trang 212 SGK Toán 12 NC
Bài tập 9 trang 212 SGK Toán 12 NC
Bài tập 11 trang 213 SGK Toán 12 NC
Bài tập 12 trang 213 SGK Toán 12 NC
Bài tập 13 trang 213 SGK Toán 12 NC
Bài tập 14 trang 213 SGK Toán 12 NC
Bài tập 15 trang 213 SGK Toán 12 NC
Bài tập 16 trang 213 SGK Toán 12 NC
Bài tập 17 trang 213 SGK Toán 12 NC
Bài tập 18 trang 214 SGK Toán 12 NC
Bài tập 19 trang 214 SGK Toán 12 NC
Bài tập 20 trang 214 SGK Toán 12 NC
Bài tập 21 trang 214 SGK Toán 12 NC
Bài tập 22 trang 214 SGK Toán 12 NC
Bài tập 23 trang 214 SGK Toán 12 NC
Bài tập 24 trang 214 SGK Toán 12 NC
Bài tập 25 trang 215 SGK Toán 12 NC
Bài tập 26 trang 214 SGK Toán 12 NC
Bài tập 27 trang 215 SGK Toán 12 NC
Bài tập 28 trang 215 SGK Toán 12 NC
Bài tập 29 trang 215 SGK Toán 12 NC
Bài tập 30 trang 215 SGK Toán 12 NC
Bài tập 31 trang 216 SGK Toán 12 NC
Bài tập 32 trang 216 SGK Toán 12 NC
Bài tập 33 trang 216 SGK Toán 12 NC
Bài tập 34 trang 216 SGK Toán 12 NC
Bài tập 35 trang 216 SGK Toán 12 NC
Bài tập 36 trang 217 SGK Toán 12 NC
Bài tập 37 trang 217 SGK Toán 12 NC
Bài tập 38 trang 217 SGK Toán 12 NC
Bài tập 1 trang 216 SBT Toán 12
Bài tập 2 trang 216 SBT Toán 12
Bài tập 3 trang 216 SBT Toán 12
Bài tập 4 trang 216 SBT Toán 12
Bài tập 5 trang 216 SBT Toán 12
Bài tập 6 trang 216 SBT Toán 12
Bài tập 7 trang 216 SBT Toán 12
Bài tập 8 trang 217 SBT Toán 12
Bài tập 9 trang 217 SBT Toán 12
Bài tập 10 trang 217 SBT Toán 12
Bài tập 11 trang 217 SBT Toán 12
Bài tập 12 trang 218 SBT Toán 12
Bài tập 13 trang 218 SBT Toán 12
Bài tập 14 trang 218 SBT Toán 12
Bài tập 15 trang 218 SBT Toán 12
Bài tập 16 trang 218 SBT Toán 12
Bài tập 17 trang 218 SBT Toán 12
Bài tập 18 trang 219 SBT Toán 12
Bài tập 19 trang 219 SBT Toán 12
Bài tập 20 trang 219 SBT Toán 12
Bài tập 21 trang 219 SBT Toán 12
Bài tập 22 trang 219 SBT Toán 12
Bài tập 23 trang 220 SBT Toán 12
Bài tập 24 trang 220 SBT Toán 12
Bài tập 25 trang 220 SBT Toán 12
-


Cho hàm số \(y = {\rm{\;}} - {x^4} + 2{x^2} + 3.\) Biết mệnh đề nào sau đây là đúng?
bởi thùy trang
 10/06/2021
10/06/2021
A. Đồ thị hàm số có 1 điểm cực đại và không có điểm cực tiểu.
B. Đồ thị hàm số có 1 điểm cực tiểu và 2 điểm cực đại.
C. Đồ thị hàm số có 1 điểm cực tiểu và không có điểm cực đại.
D. Đồ thị hàm số có 1 điểm cực đại và 2 điểm cực tiểu.
Theo dõi (0) 1 Trả lời -


Tính được giá trị nhỏ nhất của hàm số \(y = \dfrac{1}{4}{x^4} - \dfrac{{27}}{2}{x^2} + 3\) trên đoạn \(\left[ {0;80} \right]\) bằng:
bởi hà trang
 10/06/2021
10/06/2021
A. \( - \dfrac{{229}}{5}.\) B. \( - 180.\) C. \( - \dfrac{{717}}{4}.\) D. 3.
Theo dõi (0) 1 Trả lời -


Có bao nhiêu tiếp tuyến của đồ thị hàm số sau \(y = {x^3} - 3x + 2\) song song với đường thẳng \(y = 9x - 14.\)
bởi Hoang Viet
 10/06/2021
10/06/2021
A. \(1\) B. \(0\) C. \(3\) D. \(2\)
Theo dõi (0) 1 Trả lời -


Tập hợp tất cả các giá trị thực của tham số để đường thẳng \(y = - 2x + m\) cắt đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) tại hai điểm phân biệt là đáp án
bởi Nhật Mai
 11/06/2021
11/06/2021
A. \(\left( { - \infty ;5 - 2\sqrt 6 } \right) \cup \left( {5 + 2\sqrt 6 ; + \infty } \right).\)
B. \(\left( { - \infty ;5 - 2\sqrt 6 } \right] \cup \left[ {5 + 2\sqrt 6 ; + \infty } \right).\)
C. \(\left( {5 - 2\sqrt 3 ;5 + 2\sqrt 3 } \right).\)
D. \(\left( { - \infty ;5 - 2\sqrt 3 } \right) \cup \left( {5 + 2\sqrt 3 ; + \infty } \right).\)
Theo dõi (0) 1 Trả lời -
ADMICRO


Biết rằng phương trình \(\sqrt {2 - x} + \sqrt {2 + x} - \sqrt {4 - {x^2}} = m\) có nghiệm khi \(m \in \left[ {a;b} \right]\) với \(a,b \in \mathbb{R}\). Khi đó giá trị của \(T = (a + 2)\sqrt 2 + b\) là câu
bởi Thu Hang
 10/06/2021
10/06/2021
A. \(T = 3\sqrt 2 + 2\) B. \(T = 6\). C. \(T = 8\). D. \(T = 0\).
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và đồ thị như hình bên. Số nghiệm dương phân biệt của phương trình \(2f\left( x \right) + 7 = 0\) là
bởi Lê Tấn Thanh
 11/06/2021
11/06/2021
.jpg)
A. 1 B. 4 C. 2 D. 3
Theo dõi (0) 1 Trả lời -


Cho hàm số sau \(y = \dfrac{{{x^3}}}{3} + 3{x^2} - 2\) có đồ thị là \(\left( C \right)\). Viết phương trình tiếp tuyến với đồ thị \(\left( C \right)\) biết tiếp tuyến có hệ số góc \(k = {\rm{\;}} - 9?\)
bởi minh vương
 11/06/2021
11/06/2021
A. \(y + 16 = {\rm{\;}} - 9\left( {x + 3} \right)\) B. \(y = {\rm{\;}} - 9\left( {x + 3} \right)\)
C. \(y - 16 = {\rm{\;}} - 9\left( {x - 3} \right)\) D. \(y - 16 = {\rm{\;}} - 9\left( {x + 3} \right)\)
Theo dõi (0) 1 Trả lời -


Gọi \(A,{\mkern 1mu} {\mkern 1mu} B\) là hai điểm cực trị của đồ thị hàm số \(y = {x^3} - 3x - 2\). Phương trình đường thẳng đi qua hai điểm \(A,{\mkern 1mu} {\mkern 1mu} B\) là đáp án?
bởi thanh hằng
 11/06/2021
11/06/2021
A. \(x + y + 1 = 0.\) B. \(4x + y = 0.\)
C. \(2x + y + 2 = 0.\) D. \(x + y + 2 = 0.\)
Theo dõi (0) 1 Trả lời -


Hãy tìm \(m\) để đường thẳng \(y = 2x + m\) cắt đồ thị hàm số \(y = \dfrac{{x + 3}}{{x + 1}}\) tại hai điểm \(M,\;N\) sao cho độ dài MN nhỏ nhất:
bởi Minh Tuyen
 11/06/2021
11/06/2021
A. 3 B. -1 C. 2 D. 1
Theo dõi (0) 1 Trả lời -


Khẳng định nào đã cho dưới đây về hàm số \(y = {\rm{\;}} - {x^4} - 3{x^2} + 2\) là đúng?
bởi Hoa Lan
 10/06/2021
10/06/2021
A. Hàm số đạt cực tiểu tại \(x = 0\) B. hàm số có cực đại, không có cực tiểu
C. Hàm số có một cực đại và 2 cực tiểu D. Hàm số không có cực trị
Theo dõi (0) 1 Trả lời -


Cho biết hàm số \(y = f(x)\) có đạo hàm \(f'\left( x \right) = 2018{\left( {x - 1} \right)^{2017}}{\left( {x - 2} \right)^{2018}}{\left( {x - 3} \right)^{2019}}\). Tìm số điểm cực trị của \(f(x)\).
bởi Mai Thuy
 10/06/2021
10/06/2021
A. 0 B. 1 C. 2 D. 3
Theo dõi (0) 1 Trả lời -


Ta gọi \(A\left( {{x_1};{y_1}} \right)\), \(B\left( {{x_2};{y_2}} \right)\) là hai điểm cực trị của đồ thị hàm số \(y = {x^3} - 3x - 2\). Giá trị \({y_1} + {y_2}\) bằng
bởi Nguyen Phuc
 11/06/2021
11/06/2021
A. 0. B. 3. C. \( - 2.\) D. \( - 4.\)
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\left( {a;b} \right)\). Cho biết phát biểu nào sau đây là sai?
bởi Kieu Oanh
 10/06/2021
10/06/2021
A. \(f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)\) thì hàm số \(y = f\left( x \right)\) gọi là nghịch biến trên
B. Hàm số \(y = f\left( x \right)\) gọi là nghịch biến trên \(\left( {a;b} \right)\) khi và chỉ khi \(f'\left( x \right) \le 0,\forall x \in \left( {a;b} \right)\) và \(f'\left( x \right) = 0\) tại hữu hạn giá trị .
C. Hàm số \(y = f\left( x \right)\) gọi là nghịch biến trên \(\left( {a;b} \right)\) khi và chỉ khi \(\forall {x_1};{x_2} \in \left( {a;b} \right):{x_1} > {x_2} \Leftrightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right).\)
D. Hàm số \(y = f\left( x \right)\) gọi là nghịch biến trên \(\left( {a;b} \right)\) khi và chỉ khi \(f'\left( x \right) \le 0,\forall x \in \left( {a;b} \right)\).
Theo dõi (0) 1 Trả lời -


Hãy tìm giá trị nhỏ nhất của hàm số \(y = \dfrac{{{x^2} - 5}}{{x + 3}}\) trên \(\left[ {0;2} \right].\)
bởi Anh Trần
 11/06/2021
11/06/2021
A. \(\mathop {\min }\limits_{x \in \left[ {0;2} \right]} {\mkern 1mu} y = \dfrac{{ - 5}}{3}\)
B. \(\mathop {\min }\limits_{x \in \left[ {0;2} \right]} {\mkern 1mu} y = \dfrac{{ - 1}}{3}\)
C. \(\mathop {\min }\limits_{x \in \left[ {0;2} \right]} {\mkern 1mu} y = - 2\)
D. \(\mathop {\min }\limits_{x \in \left[ {0;2} \right]} {\mkern 1mu} y = - 10\)
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = \dfrac{{x + 3}}{{ - 1 - x}}\). Tìm mệnh đề đúng trong các mệnh đề sau:
bởi Dell dell
 11/06/2021
11/06/2021
A. Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
B. Hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
C. Hàm số đồng biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}\).
D. Hàm số đồng biến trên \(\left( {2; + \infty } \right)\).
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm là \(f'\left( x \right) = {\rm{\;}} - \left( {x - 10} \right){\left( {x - 11} \right)^2}{\left( {x - 12} \right)^{2019}}\) . Khẳng định nào dưới đây đúng ?
bởi thủy tiên
 11/06/2021
11/06/2021
A. Hàm số đồng biến trên các khoảng \(\left( {10;11} \right)\) và \(\left( {12; + \infty } \right)\)
B. Hàm số có ba điểm cực trị
C. Hàm số đồng biến trên khoảng \(\left( {10;12} \right)\)
D. Hàm số đạt cực đại tại \(x = 2\) và đạt cực tiểu tại \(x = 1\) và \(x = 3.\)
Theo dõi (0) 1 Trả lời -


Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = 2{x^3} + 3{x^2} - 1\) trên đoạn\(\left[ { - 2; - \dfrac{1}{2}} \right]\). Thì khi đó \(P = M - m\).
bởi con cai
 11/06/2021
11/06/2021
A. \(P = {\rm{\;}} - 5\) B. \(P = 1\) C. \(P = 5\) D. \(P = 4\)
Theo dõi (0) 1 Trả lời -


Gọi I là tâm đối xứng của đồ thị hàm số sau \(y = \dfrac{{2x - 3}}{{x + 2}}\). Tìm tọa độ điểm \(I\).
bởi Nguyen Phuc
 11/06/2021
11/06/2021
A. \(I\left( { - 2;2} \right)\)
B. \(I\left( { - 2;1} \right)\).
C. \(I\left( {1;2} \right)\)
D. \(I\left( { - 2; - \dfrac{3}{2}} \right)\).
Theo dõi (0) 1 Trả lời


