Bài tập 8 trang 217 SBT Toán 12
Cho hàm số \(y = {1 \over 3}{x^3} - (m - 1){x^2} + (m - 3)x + 4{1 \over 2}\) (m là tham số) (1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) khi m = 0.
b) Viết phương trình của tiếp tuyến với đồ thị (C) tại điểm \(A(0;4{1 \over 2})\)
c) Tính diện tích hình phẳng giới hạn bởi (C), trục hoành và các đường thẳng x = 0 và x = 2.
d) Xác định m để đồ thị của (1) cắt đường thẳng \(y = - 3x + 4{1 \over 2}\) tại ba điểm phân biệt.
Hướng dẫn giải chi tiết Bài tập 8 trang 217
a) \(y = {1 \over 3}{x^3} + {x^2} - 3x + 4{1 \over 2}\)
+) Tập xác định: D = R
+) Sự biến thiên: y’ = x2 + 2x – 3
\(y' = 0\Leftrightarrow \left[ {\matrix{{x = 1} \cr {x = - 3} \cr} } \right.\)
Bảng biến thiên:
Hàm số đồng biến trên các khoảng (-∞; -3) và (1; +∞), nghịch biến trên khoảng (-3; 1).
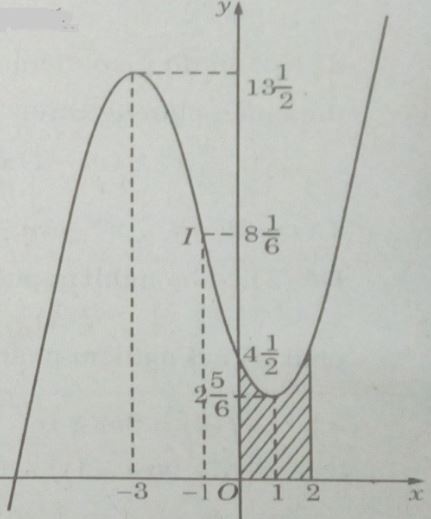
Hàm số đạt cực đại tại \(x = - 3;{y_{CD}} = 13{1 \over 2};{y_{CT}} = 2{5 \over 6}\) khi x = 1
Đồ thị cắt trục tung tại điểm \((0;4{1 \over 2})\) và có dạng như hình dưới đây.
\(y’’ = 2x + 2 ; y’’ = 0 \Leftrightarrow x = -1.\) Vậy là tâm đối xứng của đồ thị.
b) \(f(x) = {1 \over 3}{x^3} + {x^2} - 3x + 4{1 \over 2}\)
f’(x)= x2 + 2x – 3
Ta có: \(f'\left( 0 \right) = - 3\)
Tiếp tuyến với (C) tại \(A(0;4{1 \over 2})\) có phương trình là: \(y =-3(x-0) + 4{1 \over 2}\) hay \(y = - 3x + 4\dfrac{1}{2}\)
Vậy phương trình tiếp tuyến là \(y = - 3x + 4\dfrac{1}{2}\).
c) \(S = \int\limits_0^2 {({1 \over 3}{x^3} + {x^2} - 3x + 4{1 \over 2})dx } \)
\( = \left. {\left( {\dfrac{1}{3}.\dfrac{{{x^4}}}{4} + \dfrac{{{x^3}}}{3} - 3.\dfrac{{{x^2}}}{2} + 4\dfrac{1}{2}x} \right)} \right|_0^2 \) \(= 7 - 0 = 7\) (đơn vị diện tích).
d) Hoành độ giao điểm của đường thẳng \(y = - 3x + 4{1 \over 2}\) với đồ thị của (1) thỏa mãn phương trình
\({1 \over 3}{x^3} - (m - 1){x^2} + (m - 3)x + 4{1 \over 2} \) \(= - 3x + 4{1 \over 2}\) (2)
Ta có \((2)\Leftrightarrow {1 \over 3}{x^3} - (m - 1){x^2} + mx = 0\)
\(\Leftrightarrow x{\rm{[}}{x^2} - 3(m - 1)x + 3m] = 0\)
Để (2) có ba nghiệm phân biệt thì phương trình f(x) = x2– 3(m – 1)x + 3m = 0 phải có hai nghiệm phân biệt khác 0, tức là:
\(\left\{ {\matrix{{f(0) = 3m \ne 0} \cr {\Delta = 9{{(m - 1)}^2} - 12m > 0} \cr} } \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}
m \ne 0\\
9{m^2} - 18m + 9 - 12m > 0
\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}
m \ne 0\\
9{m^2} - 30m + 9 > 0
\end{array} \right. \) \( \Leftrightarrow \left\{ \begin{array}{l}
m \ne 0\\
\left[ \begin{array}{l}
m > 3\\
m < \dfrac{1}{3}
\end{array} \right.
\end{array} \right. \) \( \Leftrightarrow \left[ \begin{array}{l}
m > 3\\
0 \ne m < \dfrac{1}{3}
\end{array} \right.\)
Vậy \(m>3\) hoặc \(m < \dfrac{1}{3}\) và \(m\ne 0\).
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 6 trang 216 SBT Toán 12
Bài tập 7 trang 216 SBT Toán 12
Bài tập 9 trang 217 SBT Toán 12
Bài tập 10 trang 217 SBT Toán 12
Bài tập 11 trang 217 SBT Toán 12
Bài tập 12 trang 218 SBT Toán 12
Bài tập 13 trang 218 SBT Toán 12
Bài tập 14 trang 218 SBT Toán 12
Bài tập 15 trang 218 SBT Toán 12
Bài tập 16 trang 218 SBT Toán 12
Bài tập 17 trang 218 SBT Toán 12
Bài tập 18 trang 219 SBT Toán 12
Bài tập 19 trang 219 SBT Toán 12
Bài tập 20 trang 219 SBT Toán 12
Bài tập 21 trang 219 SBT Toán 12
Bài tập 22 trang 219 SBT Toán 12
Bài tập 23 trang 220 SBT Toán 12
Bài tập 24 trang 220 SBT Toán 12
Bài tập 25 trang 220 SBT Toán 12
-


Hãy tìm số phức liên hợp của số phức \(z = 1 - 2i\)
bởi Mai Linh
 25/05/2021
25/05/2021
A. \(2 - i\)
B. \( - 1 - 2i\)
C. \( - 1 + 2i\)
D. \(1 + 2i\)
Theo dõi (0) 1 Trả lời -


Trong không gian Oxyz, mặt cầu \(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 2} \right)^2} = 9\) có tâm và bán kính lần lượt là đáp án
bởi Dương Minh Tuấn
 25/05/2021
25/05/2021
A. \(I\left( { - 1;3;2} \right),\,\,R = 9\)
B. \(I\left( { - 1;3;2} \right),\,\,R = 3\)
C. \(I\left( {1;3;2} \right),\,\,R = 3\)
D. \(I\left( {1; - 3; - 2} \right),\,\,R = 9\)
Theo dõi (0) 1 Trả lời -


A. -2
B. \(2i\)
C. \( - 2i\)
D. 1
Theo dõi (0) 1 Trả lời -


Cho biết mô đun của số phức \(z = 5 - 4i\)
bởi Mai Linh
 25/05/2021
25/05/2021
A. 9
B. 3
C. \(\sqrt {41} \)
D. 1
Theo dõi (0) 1 Trả lời -
ADMICRO


Trong không gian Oxyz. Hãy tìm một vectơ chỉ phương của đường thẳng d: \(\frac{{x - 4}}{7} = \frac{{y - 5}}{4} = \frac{{z + 7}}{{ - 5}}\)
bởi Sam sung
 25/05/2021
25/05/2021
A. \(\mathop u\limits^ \to = \left( {7; - 4; - 5} \right)\)
B. \(\mathop u\limits^ \to = \left( {5; - 4; - 7} \right)\)
C. \(\mathop u\limits^ \to = \left( {4;5; - 7} \right)\)
D. \(\mathop u\limits^ \to = \left( {14;8; - 10} \right)\)
Theo dõi (0) 1 Trả lời -


Hãy viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị các hàm số \(y = f\left( x \right),\) \(y = g\left( x \right)\) và các đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\).
bởi Tieu Dong
 24/05/2021
24/05/2021
A. \(\int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
B. \(\int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \)
C. \(\left| {\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\)
D. \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \)
Theo dõi (0) 1 Trả lời -


A. \(\frac{{{x^3}}}{3} + 3x + C\)
B. \({x^3} + 3x + C\)
C. \(\frac{{{x^3}}}{2} + 3x + C\)
D. \({x^2} + 3x + C\)
Theo dõi (0) 1 Trả lời -


Hãy tìm môđun của số phức sau: \({z_2} = \sqrt 3 - \sqrt 7 i\)
Theo dõi (0) 1 Trả lời -


Hãy tìm môđun của số phức sau: \({z_1} = - 8 + {1 \over 2}i\)
Theo dõi (0) 1 Trả lời -


Cho biết với những giá trị thực nào của x và y thì các số phức : \({z_1} = 9{y^2} - 4 - 10x{i^5}\) và \({z_2} = 8{y^2} + 20{i^{11}}\) là liên hợp của nhau?
bởi Nhật Duy
 24/05/2021
24/05/2021
Cho biết với những giá trị thực nào của x và y thì các số phức : \({z_1} = 9{y^2} - 4 - 10x{i^5}\) và \({z_2} = 8{y^2} + 20{i^{11}}\) là liên hợp của nhau?
Theo dõi (0) 1 Trả lời -


Hãy giải hệ phương trình sau: \(\left\{ {\matrix{{x + 2y = 1 + i} \cr {3x + iy = 2 - 3i} \cr} } \right.\)
bởi Tường Vi
 24/05/2021
24/05/2021
Hãy giải hệ phương trình sau: \(\left\{ {\matrix{{x + 2y = 1 + i} \cr {3x + iy = 2 - 3i} \cr} } \right.\)
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(x^2 – x + 9 = 0 \)
bởi Hữu Trí
 24/05/2021
24/05/2021
Giải phương trình sau: \(x^2 – x + 9 = 0 \)
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(3x^2 – 4x + 2 = 0\)
bởi Van Tho
 25/05/2021
25/05/2021
Giải phương trình sau: \(3x^2 – 4x + 2 = 0\)
Theo dõi (0) 1 Trả lời -


Hãy tính: \(\displaystyle {{3 - i} \over i} + {(5 - i)^2}\)
Theo dõi (0) 1 Trả lời -


Hãy tính: \(\displaystyle {{5 + 2i} \over {7 - i}}\)
bởi Thu Hang
 24/05/2021
24/05/2021
Hãy tính: \(\displaystyle {{5 + 2i} \over {7 - i}}\)
Theo dõi (0) 1 Trả lời -


Hãy tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: \(2 \le |z - 1 + 2i| < 3\)
bởi Mai Trang
 25/05/2021
25/05/2021
Hãy tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: \(2 \le |z - 1 + 2i| < 3\)
Theo dõi (0) 1 Trả lời -


Hãy tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: |2 + z| < |2 – z|
bởi Dell dell
 24/05/2021
24/05/2021
Hãy tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: |2 + z| < |2 – z|
Theo dõi (0) 1 Trả lời -


Hãy tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: |z – i| = 1
bởi Chai Chai
 24/05/2021
24/05/2021
Hãy tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: |z – i| = 1
Theo dõi (0) 1 Trả lời