Giải bài 4 tr 43 sách GK Toán GT lớp 12
Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:
a) \(\small x^3 - 3x^2 + 5 = 0\).
b) \(\small -2x^3 + 3x^2 - 2 = 0\).
c) \(\small 2x^2 - x^4 = -1\).
Hướng dẫn giải chi tiết bài 4
Nhận xét và phương pháp giải:
Thực chất yêu cầu bài tập 3 là khảo sát sự biến thiên và vẽ đồ thị hàm số. Sau đó từ đồ thị hàm số suy ra số nghiệm của phương trình cần tìm.
Số nghiệm của các phương trình đã cho chính là số giao điểm của đồ thị hàm số y = f(x) ở vế trái của phương trình cới trục hoành ở câu a, b và với đường thẳng y = -1 ở câu c.
Lời giải:
Câu a:
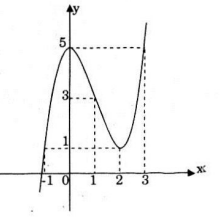
Xét hàm số \(y=x^3 - 3x^2 + 5\)
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty .\)
Sự biến thiên:
Đạo hàm: y' = 3x2 - 6x = 3x(x - 2); y' = 0 ⇔ x = 0, x = 2.
Bảng biến thiên:
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\); nghịch biến trên khoảng (0;2).
Cực trị: Hàm số đạt cực đại tại x = 0, giá trị cực đại yCĐ = y(0) = 5; đạt cực tiểu tại x = 2, giá trị cực tiểu yCT = y(2) = 1.
Đồ thị:
Tính đối xứng: y'' = 6x - 6; y'' = 0 ⇔ x = 1. Vậy đồ thị hàm số nhận điểm (1;3) làm tâm đối xứng.
Đồ thị hàm số cắt trục Oy tại điểm (0;5).
Đồ thị hàm số đi qua các điểm (-1;1); (3;5).
Đồ thị của hàm số:
Từ đồ thị ta thấy phương trình \(\small x^3 - 3x^2 + 5 = 0\) có duy nhất một nghiệm.
Câu b:
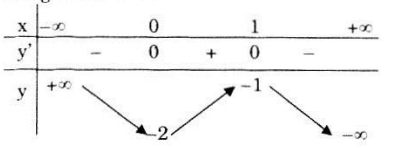
Xét hàm số y = -2x3 + 3x2 - 2
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty .\)
Sự biến thiên:
Đạo hàm: y' = -6x2 + 6x = -6x(x - 1); y' = 0 ⇔ x = 0,x = 1.
Bảng biến thiên:
Hàm số đồng biến trên khoảng (0;1); nghịch biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {1; + \infty } \right).\)
Cực trị: Hàm số đạt cực đại tại x = 1, giá trị cực đại yCĐ = y(1) = -1, hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu yCT = y(0) = -2.
Đồ thị hàm số:
Tính đối xứng:
\(y''=-12x+6;y''=0\Leftrightarrow x=\frac{1}{2}.\)
Nên tọa độ tâm đối xứng là \(I\left ( \frac{1}{2};-\frac{3}{2} \right ).\)
Đồ thị hàm số đi qua các điểm: (-1;3); (2;-6).
Đồ thị của hàm số:
Từ đồ thị hàm số ta thấy phương trình \(\small -2x^3 + 3x^2 - 2 = 0\) có nghiệm duy nhất.
Câu c:
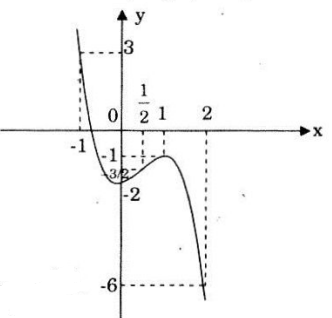
Xét hàm số y = f(x) = 2x2 - 2x4
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty .\)
Sự biến thiên:
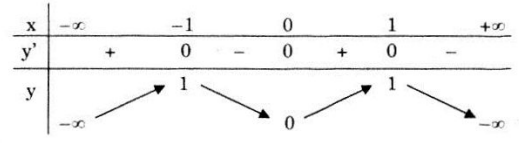
Đạo hàm: y' = 4x - 4x3 = 4x(1 - x2); y' = 0 ⇔ x = 0,x = ±1.
Bảng biến thiên:
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và (0;1); nghịch biến trên các khoảng (-1;0) và \(\left( {1; + \infty } \right).\)
Cực trị: Hàm số đạt cực đại tại x = -1 và x = 1, giá trị cực đại yCĐ = y(-1) = y(1) = 1; đạt cực tiểu tại x = 0, giá trị cực tiểu yCT = y(0) = 0.
Đồ thị:
Tính đối xứng: Đồ thị hàm số nhận trục Oy làm trục đối xứng.
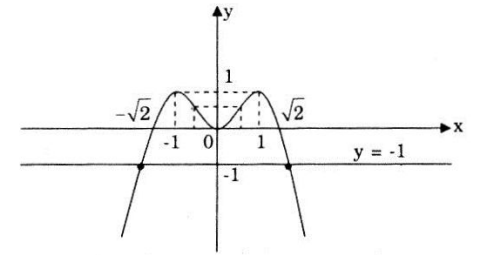
Đồ thị hàm số cắt trục Ox tại điểm (0;0); \(\left( {-\sqrt 2;0 } \right)\) và \(\left( {\sqrt 2;0 } \right)\); cắt truc Oy tại điểm (0;0).
Đồ thị của hàm số:
Đồ thị hàm số f(x) và đường thẳng y = - 1 như hình bên.
Từ đồ thị ta thấy phương trình đã cho có hai nghiệm phân biệt.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 2 trang 43 SGK Giải tích 12
Bài tập 3 trang 43 SGK Giải tích 12
Bài tập 5 trang 44 SGK Giải tích 12
Bài tập 6 trang 44 SGK Giải tích 12
Bài tập 7 trang 44 SGK Giải tích 12
Bài tập 8 trang 44 SGK Giải tích 12
Bài tập 9 trang 44 SGK Giải tích 12
Bài tập 1.56 trang 36 SBT Toán 12
Bài tập 1.57 trang 36 SBT Toán 12
Bài tập 1.58 trang 36 SBT Toán 12
Bài tập 1.59 trang 36 SBT Toán 12
Bài tập 1.60 trang 36 SBT Toán 12
Bài tập 1.61 trang 36 SBT Toán 12
Bài tập 1.62 trang 37 SBT Toán 12
Bài tập 1.63 trang 37 SBT Toán 12
Bài tập 1.64 trang 37 SBT Toán 12
Bài tập 1.65 trang 37 SBT Toán 12
Bài tập 1.66 trang 38 SBT Toán 12
Bài tập 1.67 trang 38 SBT Toán 12
Bài tập 1.68 trang 38 SBT Toán 12
Bài tập 1.69 trang 38 SBT Toán 12
Bài tập 1.70 trang 38 SBT Toán 12
Bài tập 1.71 trang 39 SBT Toán 12
Bài tập 1.72 trang 39 SBT Toán 12
Bài tập 1.73 trang 39 SBT Toán 12
Bài tập 1.74 trang 39 SBT Toán 12
Bài tập 29 trang 27 SGK Toán 12 NC
Bài tập 30 trang 27 SGK Toán 12 NC
Bài tập 31 trang 27 SGK Toán 12 NC
Bài tập 32 trang 28 SGK Toán 12 NC
Bài tập 33 trang 28 SGK Toán 12 NC
Bài tập 40 trang 43 SGK Toán 12 NC
Bài tập 41 trang 44 SGK Toán 12 NC
Bài tập 42 trang 45 SGK Toán 12 NC
Bài tập 43 trang 44 SGK Toán 12 NC
Bài tập 44 trang 44 SGK Toán 12 NC
Bài tập 45 trang 44 SGK Toán 12 NC
Bài tập 46 trang 44 SGK Toán 12 NC
Bài tập 47 trang 45 SGK Toán 12 NC
Bài tập 48 trang 45 SGK Toán 12 NC
Bài tập 49 trang 49 SGK Toán 12 NC
Bài tập 50 trang 49 SGK Toán 12 NC
Bài tập 51 trang 49 SGK Toán 12 NC
Bài tập 52 trang 50 SGK Toán 12 NC
Bài tập 53 trang 50 SGK Toán 12 NC
Bài tập 54 trang 50 SGK Toán 12 NC
Bài tập 55 trang 50 SGK Toán 12 NC
Bài tập 56 trang 50 SGK Toán 12 NC
Bài tập 57 trang 55 SGK Toán 12 NC
Bài tập 58 trang 56 SGK Toán 12 NC
Bài tập 59 trang 56 SGK Toán 12 NC
Bài tập 60 trang 56 SGK Toán 12 NC
Bài tập 61 trang 56 SGK Toán 12 NC
Bài tập 62 trang 57 SGK Toán 12 NC
Bài tập 63 trang 57 SGK Toán 12 NC
Bài tập 64 trang 57 SGK Toán 12 NC
-


Cho biết hàm số: \(y = {x^3} - (m + 4){x^2} - 4x + m\). Chứng minh rằng với mọi giá trị của \(m\), đồ thị của hàm số đã cho luôn luôn có cực trị.
bởi Ha Ku
 25/09/2022
Theo dõi (0) 1 Trả lời
25/09/2022
Theo dõi (0) 1 Trả lời -


Cho biết hàm số: \(y = {x^3} - (m + 4){x^2} - 4x + m\). Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của \(m\).
bởi Mai Hoa
 25/09/2022
Theo dõi (0) 1 Trả lời
25/09/2022
Theo dõi (0) 1 Trả lời -


Em hãy tìm giá trị của tham số \(m\) để hàm số \(y = (m - 1){x^4} - m{x^2} + 3\) có đúng một cực trị.
bởi Quế Anh
 25/09/2022
Theo dõi (0) 1 Trả lời
25/09/2022
Theo dõi (0) 1 Trả lời -


Thực hiện tìm giá trị của tham số \(m\) để hàm số sau: \(y = - \dfrac{1}{3}({m^2} + 6m){x^3} - 2m{x^2} + 3x + 1\) đạt cực đại tại \(x = - 1\)
bởi Khanh Đơn
 26/09/2022
Theo dõi (0) 1 Trả lời
26/09/2022
Theo dõi (0) 1 Trả lời -
ADMICRO


Thực hiện tìm giá trị của tham số \(m\) để hàm số sau: \(y = {x^3} + (m + 3){x^2} + mx - 2\) đạt cực tiểu tại \(x = 1\)
bởi Bánh Mì
 25/09/2022
Theo dõi (0) 1 Trả lời
25/09/2022
Theo dõi (0) 1 Trả lời -


Tìm x biết: ((3x-1)^2 = (x-1)^2)
bởi Vũ Trang
 05/01/2022
05/01/2022
Tìm x biết: (3x-1)2 = (x-1)2
Theo dõi (1) 1 Trả lời -


Tìm tất cả các giá trị tham số m để bpt ({4^2} - left( {x + 1} ight){2^{x + 1}} + m ge 0) với mọi x>0
bởi Lê Đình Toản
 31/12/2021
31/12/2021
Tất cả các giá trị ts m để bpt 42-(×+1)2×+1+m ≥0 với mọi x>0
Theo dõi (0) 0 Trả lời




.PNG)