Giải bài 5 tr 44 sách GK Toán GT lớp 12
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số \(\small y = -x^3 + 3x + 1\)
b) Dựa vào đồ thị (C), biện luận về số nghiệm của phương trình sau theo tham số m.
\(\small x^3 - 3x + m = 0.\)
Hướng dẫn giải chi tiết bài 5
Nhận xét và phương pháp giải:
Câu a là một bài khảo sát sự biến thiên và vẽ đồ thị hàm tương tự câu 1 đã làm nên không nhắc lại ở đây, trọng tâm bài toán này là ở câu b.
Đây là bài toán:
Cho hàm số y = f(x) có đồ thị (C). Dựa vào đồ thị (C) biện luận số nghiệm của phương trình g(x;m) = 0 với m là tham số.
Với bài 5, ta sẽ chuyển bài toán về dạng:
f(x) = h(m), trong đó h(m) là một hàm phụ thuộc vào tham số m.
- Vẽ đồ thị hàm số y = f(x).
- Đường thẳng y = h(m) di động song song với trục hoành, dựa vào số giao diểm của đường thẳng y = h(m) với đồ thị hàm số y = f(x) để suy ra số nghiệm của phương trình g(x;m) = 0.
Đó là phương pháp để giải bài toán này, có thể nhiều em khi đọc qua phần lý thuyết này vẫn chưa hình dung được phải làm như thế nào. Vậy xin mời các em tham khảo lời giải chi tiết sau để hiểu và nắm phương pháp làm bài.
Lời giải:
Câu a:
Với m = 1 ta có hàm số: y = -x3 + 3x + 1
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty .\)
Sự biến thiên:
Đạo hàm: y' = -3x2 + 3 = -3(x2 - 1); y' = 0 ⇔ x = -1, x = 1.
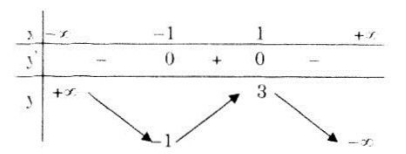
Bảng biến thiên:
Hàm số đồng biến trên khoảng (-1;1), nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right).\)
Cực trị: Hàm số đạt cực đại tại x=1, giá trị cực tiểu yCĐ = y(1) = 3; đạt cực tiểu tại x = - 1, giá trị cực tiểu yCT = y(-1) = -1.
Đồ thị:
Tính đối xứng: y'' = - 6x, y'' = 0 ⇔ x = 0. Vậy tọa độ tâm đối xứng của đồ thị hàm số là (0;1).
Đồ thị hàm số đi qua các điểm (-2;3); (2;-1).
Đồ thị hàm số:
Câu b:
Xét phương trình x3 - 3x + m = 0 ⇔ - x3 + 3x + 1 = m + 1 (1).
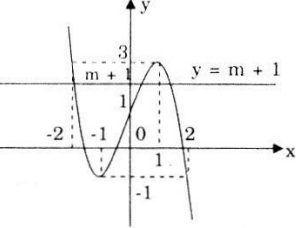
Số nghiệm của (1) chính là số giao điểm của đồ thị (C) với đường thẳng (d): y = m + 1.
Từ đồ thị ta thấy :
- Khi: m + 1 < -1 ⇔ m < -2: (d) cắt (C) tại 1 điểm suy ra (1) có 1 nghiệm.
- Khi: m + 1 = -1 ⇔ m = -2: (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm suy ra (1) có 2 nghiệm.
- Khi: -1 < m + 1 < 3 ⇔ -2 < m < 2: (d) cắt (C) tại 3 điểm suy ra (1) có 3 nghiệm.
- Khi: m + 1 = 3 ⇔ m = 2: (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm suy ra (1) có 2 nghiệm.
- Khi: m + 1 > 3 ⇔ m > 2: (d) cắt (C) tại 1 điểm suy ra (1) có 1 nghiệm.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3 trang 43 SGK Giải tích 12
Bài tập 4 trang 43 SGK Giải tích 12
Bài tập 6 trang 44 SGK Giải tích 12
Bài tập 7 trang 44 SGK Giải tích 12
Bài tập 8 trang 44 SGK Giải tích 12
Bài tập 9 trang 44 SGK Giải tích 12
Bài tập 1.56 trang 36 SBT Toán 12
Bài tập 1.57 trang 36 SBT Toán 12
Bài tập 1.58 trang 36 SBT Toán 12
Bài tập 1.59 trang 36 SBT Toán 12
Bài tập 1.60 trang 36 SBT Toán 12
Bài tập 1.61 trang 36 SBT Toán 12
Bài tập 1.62 trang 37 SBT Toán 12
Bài tập 1.63 trang 37 SBT Toán 12
Bài tập 1.64 trang 37 SBT Toán 12
Bài tập 1.65 trang 37 SBT Toán 12
Bài tập 1.66 trang 38 SBT Toán 12
Bài tập 1.67 trang 38 SBT Toán 12
Bài tập 1.68 trang 38 SBT Toán 12
Bài tập 1.69 trang 38 SBT Toán 12
Bài tập 1.70 trang 38 SBT Toán 12
Bài tập 1.71 trang 39 SBT Toán 12
Bài tập 1.72 trang 39 SBT Toán 12
Bài tập 1.73 trang 39 SBT Toán 12
Bài tập 1.74 trang 39 SBT Toán 12
Bài tập 29 trang 27 SGK Toán 12 NC
Bài tập 30 trang 27 SGK Toán 12 NC
Bài tập 31 trang 27 SGK Toán 12 NC
Bài tập 32 trang 28 SGK Toán 12 NC
Bài tập 33 trang 28 SGK Toán 12 NC
Bài tập 40 trang 43 SGK Toán 12 NC
Bài tập 41 trang 44 SGK Toán 12 NC
Bài tập 42 trang 45 SGK Toán 12 NC
Bài tập 43 trang 44 SGK Toán 12 NC
Bài tập 44 trang 44 SGK Toán 12 NC
Bài tập 45 trang 44 SGK Toán 12 NC
Bài tập 46 trang 44 SGK Toán 12 NC
Bài tập 47 trang 45 SGK Toán 12 NC
Bài tập 48 trang 45 SGK Toán 12 NC
Bài tập 49 trang 49 SGK Toán 12 NC
Bài tập 50 trang 49 SGK Toán 12 NC
Bài tập 51 trang 49 SGK Toán 12 NC
Bài tập 52 trang 50 SGK Toán 12 NC
Bài tập 53 trang 50 SGK Toán 12 NC
Bài tập 54 trang 50 SGK Toán 12 NC
Bài tập 55 trang 50 SGK Toán 12 NC
Bài tập 56 trang 50 SGK Toán 12 NC
Bài tập 57 trang 55 SGK Toán 12 NC
Bài tập 58 trang 56 SGK Toán 12 NC
Bài tập 59 trang 56 SGK Toán 12 NC
Bài tập 60 trang 56 SGK Toán 12 NC
Bài tập 61 trang 56 SGK Toán 12 NC
Bài tập 62 trang 57 SGK Toán 12 NC
Bài tập 63 trang 57 SGK Toán 12 NC
Bài tập 64 trang 57 SGK Toán 12 NC
-

 Câu 102:Đồ thị hàm sốTheo dõi (0) 1 Trả lời
Câu 102:Đồ thị hàm sốTheo dõi (0) 1 Trả lời -


Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=x + mx +1 cắt đường thẳngd : y=1 tại 3 điểm phân biệt.
bởi nguyenthanhdan
 15/10/2021
Tìm số thực mTheo dõi (0) 1 Trả lời
15/10/2021
Tìm số thực mTheo dõi (0) 1 Trả lời -


Tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số (y= x^2 -x -1) và y = 2x - 3
bởi Lê Văn Ninh
 02/07/2021
02/07/2021
Tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y= x^2 -x -1\) và y = 2x - 3
Theo dõi (1) 0 Trả lời -


Tìm cực đại các hệ số m, n, p sao cho hàm số sau \(f(x) = - {1 \over 3}{x^3} + m{x^2} + nx + p\). Đạt cực đại tại điểm x = 3 và đồ thị (C) của nó tiếp xúc với đường thẳng \(y = 3x - {1 \over 3}\) tại giao điểm của (C) với trục tung.
bởi Nguyễn Quang Minh Tú
 03/06/2021
03/06/2021
Tìm cực đại các hệ số m, n, p sao cho hàm số sau \(f(x) = - {1 \over 3}{x^3} + m{x^2} + nx + p\). Đạt cực đại tại điểm x = 3 và đồ thị (C) của nó tiếp xúc với đường thẳng \(y = 3x - {1 \over 3}\) tại giao điểm của (C) với trục tung.
Theo dõi (0) 1 Trả lời -
ADMICRO


Giao điểm của đồ thị hàm số sau \(y = \dfrac{{2x + 1}}{{2x - 1}}\) với đường thẳng \(y = x + 2\) là:
bởi Nguyễn Vân
 02/06/2021
02/06/2021
A. \(\left( {1;3} \right)\) và \(\left( { - \dfrac{3}{2};\dfrac{1}{2}} \right)\)
B. \(\left( {1;3} \right)\) và \(\left( {0;2} \right)\)
C. \(\left( {0; - 1} \right)\) và \(\left( { - \dfrac{3}{2};\dfrac{1}{2}} \right)\)
D. \(\left( {0; - 1} \right)\) và \(\left( {0;2} \right)\)
Theo dõi (0) 1 Trả lời -


Phương trình tiếp tuyến của đồ thị hàm số sau \(y = {x^4} - 2{x^2} - 3\) song song với đường thẳng \(y = 24x - 1\) là:
bởi Lê Minh
 02/06/2021
02/06/2021
A. \(y = 24x - 43\)
B. \(y = - 24x - 43\)
C. \(y = 24x + 43\)
D. \(y = 24x + 1\)
Theo dõi (0) 1 Trả lời -


Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4}-2{x^2}\) tại điểm có hoành độ \(x = - 2\) là đáp án?
bởi Nguyen Dat
 03/06/2021
03/06/2021
A. \(y = - 24x + 40\)
B. \(y = 24x - 40\)
C. \(y = - 24x - 40\)
D. \(y = - 24x\)
Theo dõi (0) 1 Trả lời