Giải bài 9 tr 44 sách GK Toán GT lớp 12
Cho hàm số \(y = \frac{{\left( {m + 1} \right)x - 2m + 1}}{{x - 1}}\) (m là tham số) có đồ thị là (G).
a) Xác định m để đồ thị (G) đi qua điểm (0 ; -1).
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m tìm được.
c) Viết phương trình tiếp tuyến của đồ thị trên tại giao điểm của nó với trục tung.
Hướng dẫn giải chi tiết bài 9
Câu a:
Đồ thị hàm số đi qua điểm (0;-1) nên ta có:
\( - 1 = \frac{{\left( {m + 1} \right).0 - 2m + 1}}{{0 - 1}} \Leftrightarrow m = 0\)
Câu b:
Với m = 0 ta có hàm số \(y = \frac{{x + 1}}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash {\rm{\{ }}1\} .\)
Giới hạn và tiệm cận:
\(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{x + 1}}{{x - 1}} = - \infty ;\)
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1}}{{x - 1}} = + \infty\)
Nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x + 1}}{{x - 1}} = 1;\)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x - 1}} = 1\)
Nên đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
Sự biến thiên:
Đạo hàm: \(y' = - \frac{2}{{{{(x - 1)}^2}}} < 0,\forall x \ne 1.\)
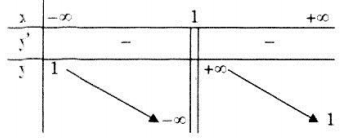
Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng: \(\left( { - \infty ;1} \right);\,\,\left( {1; + \infty } \right).\)
Hàm số không có cực trị.
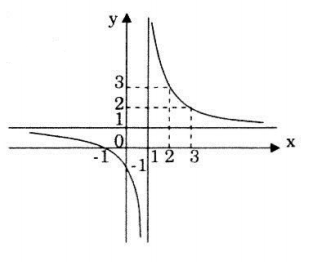
Đồ thị:
Đồ thị hàm số nhận điểm I(1;1) làm tâm đối xứng.
Đồ thị cắt trục Ox tại điểm (-1;0), cắt Oy tại điểm (0;-1).
Với x = 2 suy ra y = 3.
Với x = 3 suy ra y = 2.
Đồ thị của hàm số:
Câu c:
Đồ thị hàm số cắt trục tung tại điểm M(0;1).
Ta có: \(y' = - \frac{2}{{{{\left( {x - 1} \right)}^2}}}\) suy ra: y'(0) = - 2.
Phương trình tiếp tuyến của tại M là: y - (-1) = y'(0)(x - 0) ⇔ y = - 2x - 1.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 7 trang 44 SGK Giải tích 12
Bài tập 8 trang 44 SGK Giải tích 12
Bài tập 1.56 trang 36 SBT Toán 12
Bài tập 1.57 trang 36 SBT Toán 12
Bài tập 1.58 trang 36 SBT Toán 12
Bài tập 1.59 trang 36 SBT Toán 12
Bài tập 1.60 trang 36 SBT Toán 12
Bài tập 1.61 trang 36 SBT Toán 12
Bài tập 1.62 trang 37 SBT Toán 12
Bài tập 1.63 trang 37 SBT Toán 12
Bài tập 1.64 trang 37 SBT Toán 12
Bài tập 1.65 trang 37 SBT Toán 12
Bài tập 1.66 trang 38 SBT Toán 12
Bài tập 1.67 trang 38 SBT Toán 12
Bài tập 1.68 trang 38 SBT Toán 12
Bài tập 1.69 trang 38 SBT Toán 12
Bài tập 1.70 trang 38 SBT Toán 12
Bài tập 1.71 trang 39 SBT Toán 12
Bài tập 1.72 trang 39 SBT Toán 12
Bài tập 1.73 trang 39 SBT Toán 12
Bài tập 1.74 trang 39 SBT Toán 12
Bài tập 29 trang 27 SGK Toán 12 NC
Bài tập 30 trang 27 SGK Toán 12 NC
Bài tập 31 trang 27 SGK Toán 12 NC
Bài tập 32 trang 28 SGK Toán 12 NC
Bài tập 33 trang 28 SGK Toán 12 NC
Bài tập 40 trang 43 SGK Toán 12 NC
Bài tập 41 trang 44 SGK Toán 12 NC
Bài tập 42 trang 45 SGK Toán 12 NC
Bài tập 43 trang 44 SGK Toán 12 NC
Bài tập 44 trang 44 SGK Toán 12 NC
Bài tập 45 trang 44 SGK Toán 12 NC
Bài tập 46 trang 44 SGK Toán 12 NC
Bài tập 47 trang 45 SGK Toán 12 NC
Bài tập 48 trang 45 SGK Toán 12 NC
Bài tập 49 trang 49 SGK Toán 12 NC
Bài tập 50 trang 49 SGK Toán 12 NC
Bài tập 51 trang 49 SGK Toán 12 NC
Bài tập 52 trang 50 SGK Toán 12 NC
Bài tập 53 trang 50 SGK Toán 12 NC
Bài tập 54 trang 50 SGK Toán 12 NC
Bài tập 55 trang 50 SGK Toán 12 NC
Bài tập 56 trang 50 SGK Toán 12 NC
Bài tập 57 trang 55 SGK Toán 12 NC
Bài tập 58 trang 56 SGK Toán 12 NC
Bài tập 59 trang 56 SGK Toán 12 NC
Bài tập 60 trang 56 SGK Toán 12 NC
Bài tập 61 trang 56 SGK Toán 12 NC
Bài tập 62 trang 57 SGK Toán 12 NC
Bài tập 63 trang 57 SGK Toán 12 NC
Bài tập 64 trang 57 SGK Toán 12 NC
-


Hãy khảo sát và vẽ đồ thị hàm số: \(y = {x^3} - {x^2} + x\).
Theo dõi (0) 1 Trả lời -


Khảo sát sự biến thiên và vẽ đồ thị của hàm số sau: \(y = - x + 2 + {1 \over {x - 1}}\).
bởi hà trang
 02/06/2021
02/06/2021
Khảo sát sự biến thiên và vẽ đồ thị của hàm số sau: \(y = - x + 2 + {1 \over {x - 1}}\).
Theo dõi (0) 1 Trả lời -


Khảo sát sự biến thiên và vẽ đồ thị của hàm số sau: \(y = {{2{x^2} + 3x - 3} \over {x + 2}}\).
bởi Ngoc Son
 02/06/2021
02/06/2021
Khảo sát sự biến thiên và vẽ đồ thị của hàm số sau: \(y = {{2{x^2} + 3x - 3} \over {x + 2}}\).
Theo dõi (0) 1 Trả lời -


Khảo sát sự biến thiên và vẽ đồ thị của hàm số sau: \(y = {{2{x^2} - x + 1} \over {1 - x}}\).
bởi Nguyen Nhan
 01/06/2021
01/06/2021
Khảo sát sự biến thiên và vẽ đồ thị của hàm số sau: \(y = {{2{x^2} - x + 1} \over {1 - x}}\).
Theo dõi (0) 1 Trả lời -
ADMICRO


Khảo sát sự biến thiên và vẽ đồ thị của hàm số sau: \(y = {{{x^2} - 3x + 6} \over {x - 1}}\).
bởi Thùy Trang
 01/06/2021
01/06/2021
Khảo sát sự biến thiên và vẽ đồ thị của hàm số sau: \(y = {{{x^2} - 3x + 6} \over {x - 1}}\).
Theo dõi (0) 1 Trả lời -


Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = {{2{x^2} + 5x + 4} \over {x + 2}}\).
bởi hành thư
 01/06/2021
01/06/2021
Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = {{2{x^2} + 5x + 4} \over {x + 2}}\).
Theo dõi (0) 1 Trả lời -


Khảo sát sự biến thiên và vẽ đồ thị hàm số sau: \(y = {{2x + 1} \over {1 - 3x}}\)
bởi Anh Nguyễn
 02/06/2021
02/06/2021
Khảo sát sự biến thiên và vẽ đồ thị hàm số sau: \(y = {{2x + 1} \over {1 - 3x}}\)
Theo dõi (0) 1 Trả lời