Bài tập 29 trang 27 SGK Toán 12 NC
Xác định đỉnh I của mỗi parabol (P) sau đây. Viết công thức chuyển hệ tọa độ trong phép tịnh tiến theo vectơ \(\overrightarrow {OI} \) và viết phương trình của parabol (P) đối với hệ tọa độ IXY
a) \(y = 2{x^2} - 3x + 1\)
b) \(y = \frac{1}{2}{x^2} - x - 3\)
c) \(y = x - 4{x^2}\)
d) \(y = 2{x^2} - 5\)
Hướng dẫn giải chi tiết
a)
\(\begin{array}{l}
y\prime = 4x - 3;\\
y\prime = 0 \Leftrightarrow x = \frac{3}{4};y\left( {\frac{3}{4}} \right) = - \frac{1}{8}
\end{array}\)
Đỉnh \(I\left( {\frac{3}{4}; - \frac{1}{8}} \right)\)
Công thức chuyển trục tọa độ tịnh tiến theo
\(\overrightarrow {OI} :\left\{ \begin{array}{l}
x = X + \frac{3}{4}\\
y = Y - \frac{1}{8}
\end{array} \right.\)
Phương trình của (P) đối với tọa độ IXY là:
\(\begin{array}{l}
Y - \frac{1}{8} = 2{\left( {X + \frac{3}{4}} \right)^2} - 3\left( {X + \frac{3}{4}} \right) + 1\\
\Leftrightarrow Y = 2{X^2}
\end{array}\)
b)
\(\begin{array}{l}
y\prime = x - 1;\\
y\prime = 0 \Leftrightarrow x = 1;y(1) = - \frac{7}{2}
\end{array}\)
Đỉnh \(I\left( 1; - \frac{7}{2}} \right)\)
Công thức chuyển trục tọa độ tịnh tiến theo
\(\overrightarrow {OI} :\left\{ \begin{array}{l}
x = 1 + X\\
y = - \frac{7}{2} + Y
\end{array} \right.\)
Phương trình của (P) đối với tọa độ IXY là:
\(\begin{array}{l}
Y - \frac{7}{2} = \frac{1}{2}{(X + 1)^2} - (X + 1) - 3\\
\Leftrightarrow Y = \frac{1}{2}{X^2}
\end{array}\)
c)
\(\begin{array}{l}
y\prime = 1 - 8x;\\
y\prime = 0 \Leftrightarrow x = 18;y\left( {\frac{1}{8}} \right) = \frac{1}{{16}}
\end{array}\)
Đỉnh \(I\left( {\frac{1}{8};\frac{1}{{16}}} \right)\)
Công thức chuyển trục tọa độ tịnh tiến theo
\(\overrightarrow {OI} :\left\{ \begin{array}{l}
x = X + \frac{1}{8}\\
y = Y + \frac{1}{{16}}
\end{array} \right.\)
Phương trình của (P) đối với tọa độ IXY là:
\(Y + \frac{1}{{16}} = X + \frac{1}{8} - 4{\left( {X + \frac{1}{8}} \right)^2} \Leftrightarrow Y = - 4{X^2}\)
d) y' = 4x, y' = 0 ⇔ x = 0; y(0) = -5
Đỉnh I(0;-5)
Công thức chuyển trục tọa độ tịnh tiến theo
\(\overrightarrow {OI} :\left\{ \begin{array}{l}
x = X\\
y = Y - 5
\end{array} \right.\)
Phương trình của (P) đối với tọa độ IXY là:
\(Y - 5 = 2{X^2} - 5 \Leftrightarrow Y = 2{X^2}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 1.73 trang 39 SBT Toán 12
Bài tập 1.74 trang 39 SBT Toán 12
Bài tập 30 trang 27 SGK Toán 12 NC
Bài tập 31 trang 27 SGK Toán 12 NC
Bài tập 32 trang 28 SGK Toán 12 NC
Bài tập 33 trang 28 SGK Toán 12 NC
Bài tập 40 trang 43 SGK Toán 12 NC
Bài tập 41 trang 44 SGK Toán 12 NC
Bài tập 42 trang 45 SGK Toán 12 NC
Bài tập 43 trang 44 SGK Toán 12 NC
Bài tập 44 trang 44 SGK Toán 12 NC
Bài tập 45 trang 44 SGK Toán 12 NC
Bài tập 46 trang 44 SGK Toán 12 NC
Bài tập 47 trang 45 SGK Toán 12 NC
Bài tập 48 trang 45 SGK Toán 12 NC
Bài tập 49 trang 49 SGK Toán 12 NC
Bài tập 50 trang 49 SGK Toán 12 NC
Bài tập 51 trang 49 SGK Toán 12 NC
Bài tập 52 trang 50 SGK Toán 12 NC
Bài tập 53 trang 50 SGK Toán 12 NC
Bài tập 54 trang 50 SGK Toán 12 NC
Bài tập 55 trang 50 SGK Toán 12 NC
Bài tập 56 trang 50 SGK Toán 12 NC
Bài tập 57 trang 55 SGK Toán 12 NC
Bài tập 58 trang 56 SGK Toán 12 NC
Bài tập 59 trang 56 SGK Toán 12 NC
Bài tập 60 trang 56 SGK Toán 12 NC
Bài tập 61 trang 56 SGK Toán 12 NC
Bài tập 62 trang 57 SGK Toán 12 NC
Bài tập 63 trang 57 SGK Toán 12 NC
Bài tập 64 trang 57 SGK Toán 12 NC
-

 Giải dùm mình câu 20 với
Giải dùm mình câu 20 với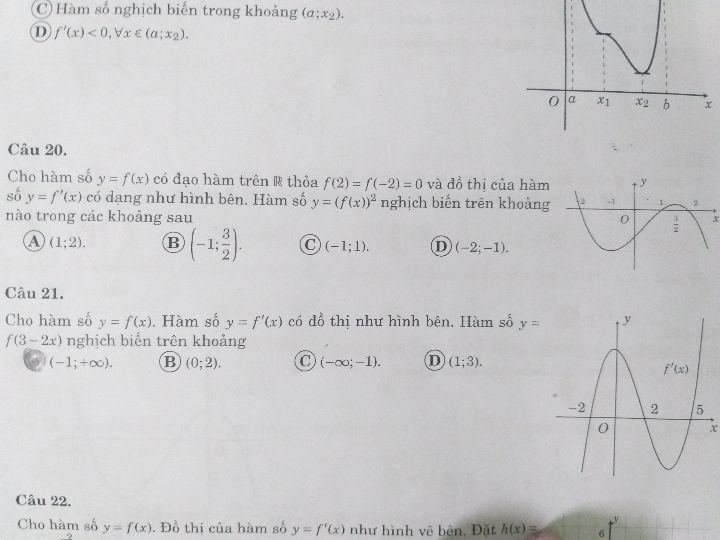 Theo dõi (2) 13 Trả lời
Theo dõi (2) 13 Trả lời -


Tìm số nghiệm của phương trình 2|f(x)-1|=0
bởi Tuệ Linh
 11/06/2019
Giúp em câu 27 với ak
11/06/2019
Giúp em câu 27 với ak Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tìm số hạng không chứa x trong khai triển (x 8/x^2)^9
bởi Trần Quỳnh
 03/06/2019
Trong khai triển (x 8/x^2)^9 số hạng không chứa x là: Dấu ^ là mũ nhé mng ơiTheo dõi (0) 9 Trả lời
03/06/2019
Trong khai triển (x 8/x^2)^9 số hạng không chứa x là: Dấu ^ là mũ nhé mng ơiTheo dõi (0) 9 Trả lời -


Tìm m để hàm số y=x^3-3(m+1)x^2+2mx+m+2 cắt trục hoành tại 3 điểm phân biệt
bởi Nguyễn Ngọc Phương Thanh
 14/12/2018
14/12/2018
Tìm điều kiện m để đồ thị hàm số y=
cắt trục hoành tại 3 điểm phân biệt biết răng đồ thị hàm số luôn đi điểm cố định (1;0)
Theo dõi (0) 4 Trả lời -
ADMICRO


Từ điểm A(1;4) có thể kẻ được bao nhiêu tiếp tuyến đến (C): y=2x^3+3x^2-1 ?
bởi Nguyễn Ngọc Phương Thanh
 14/12/2018
14/12/2018
Từ điểm A(1;4) có thể kẻ được bao nhiêu tiếp tuyến đến (C):y=
Theo dõi (0) 4 Trả lời -


Tìm m để đường thẳng y=(m-4) cắt đồ thị hàm số y=(x^2-1).(x^2-9) tại 4 điểm phân biệt
bởi Nguyên Nguyễn
 29/10/2018
29/10/2018
Tìm mm để đường thẳng y=(m−4)y=(m−4) cắt đồ thị hàm số y=(x2−1)(x2−9)y=(x2−1)(x2−9) tại 4 điểm phân biệt?
Theo dõi (0) 1 Trả lời -


Viết phương trình tiếp tuyến tại (C) tại điểm có hoành độ dương và là nghiệm của phương trình y'(x)+x.y'(x)-11=0
bởi Thoa Nguyễn
 29/10/2018
29/10/2018
Cho hàm số y = x^3-3x^2-x+1 (C). Phương trình tiếp tuyến tại (C) tại điểm có hoành độ dương và là nghiệm của phương trình y'(x)+x.y'(x)-11=0
Theo dõi (0) 1 Trả lời





