Bài tập 7 trang 44 SGK Giải tích 12

Nhận xét và phương pháp giải:

- Câu a, yêu cầu tìm tham số m để đồ thị hàm số đi qua một điểm cho trước, rất đơn giản ta chỉ cần thay tọa điểm đó vào hàm số tương ứng y là tung độ, x là hoành độ, khi đó ta chỉ cần giải phương trình tìm tham số m.

- Câu b, tham giá trị của m vào hàm số ta sẽ được một hàm số cụ thể sau đó thực hiện các bước khảo sát sự biến thiên và vẽ đồ thị hàm số này.

- Câu c, phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại tiếp điểm M(x₀,y₀) thuộc đồ thị hàm số đã học ở chương trình lớp 11 có dạng \(y-y_0=f'(x_0)(x-x_0)\)

Như vậy trong câu c, ta cần phải xác định được tọa độ tiếp điểm. Mặc khác theo đề bài ta có tung độ tiếp điểm bằng \(\frac{7}{4}\), từ đó ta thay vào hàm số sẽ được tìm hoành độ.

Lời giải:

Lời giải chi tiết câu a, b, c bài 7 như sau:

Câu a:

Điểm (-1;1) thuộc đồ thị của hàm số nên ta có:

\(1 = \frac{1}{4}{\left( { - 1} \right)^4} + \frac{1}{2}{\left( { - 1} \right)^2} + m \Leftrightarrow m = \frac{1}{4}\).

Câu b:

Với m = 1 ta có hàm số: 

\(y=\frac{1}{4}x^{4}+\frac{1}{2}x^{2}+1\) 

Tập xác định: \(D=\mathbb{R}.\)

Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty\)

Sự biến thiên:

\(y = {x^3} + x = x\left( {{x^2} + 1} \right);y' = 0 \Leftrightarrow x = 0\)

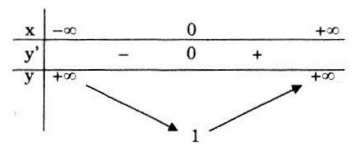
Bảng biến thiên:

Vậy hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right).\)        

Cực trị: Hàm số đạt cực tiểu tại x = 0 và giá trị cực tiểu y_CT = y(0) = 1.

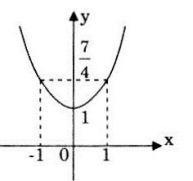
Đồ thị:

Đồ thị hàm số cắt trục Oy tại điểm (0;1).

Với x = 1 ta có \(y=\frac{7}{4}.\)

Với x = -1 ta có \(y=\frac{7}{4}.\)

Đồ thị hàm số:

Câu c:

Với \(y=\frac{7}{4}\) ta có: 

\(\begin{array}{l}
\frac{1}{4}{x^4} + \frac{1}{2}{x^2} + 1 = \frac{7}{4} \Leftrightarrow {x^4} + 2{x^2} - 3 = 0\\
 \Leftrightarrow {x^2} = 1 \Leftrightarrow x =  \pm 1
\end{array}\)
Vậy hai điểm thuộc (C) có tung độ \(y=\frac{7}{4}\) là \(A\left ( 1;\frac{7}{4} \right )\)và \(B\left ( -1;\frac{7}{4} \right )\).

Ta có: y' = x³ + x suy ra: y'(-1) = - 2, y'(1) = 2.

Phương trình tiếp tuyến với (C) tại A là: \(y - \frac{7}{4} = y'(1)(x - 1) \Leftrightarrow y = 2x - \frac{1}{4}.\)

Phương trình tiếp tuyến với (C) tại B là: \(y - \frac{7}{4} = y'(-1)(x + 1) \Leftrightarrow y = -2x - \frac{1}{4}.\)

-- Mod Toán 12 HỌC247