Giải bài 1.63 tr 37 SBT Toán 12
Cho hàm số
\(y = {x^3} - (m + 4){x^2} - 4x + m\) (1)
a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.
b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi .
d) Xác định để (C) cắt đường thẳng tại ba điểm phân biệt
Hướng dẫn giải chi tiết
a)
Ta có: \(y = {x^3} - (m + 4){x^2} - 4x + m\)
\(\begin{array}{l}
\Leftrightarrow y = {x^3} - m{x^2} - 4{x^2} - 4x + m\\
\Leftrightarrow y - {x^3} + m{x^2} + 4{x^2} + 4x - m = 0\\
\Leftrightarrow \left( {m{x^2} - m} \right) + y - {x^3} + 4{x^2} + 4x = 0
\end{array}\)
\( \Leftrightarrow \left( {{x^2} - 1} \right)m + y - {x^3} + 4{x^2} + 4x = 0\)
Đồ thị của hàm số (1) luôn luôn đi qua điểm \(A\left( {x;y} \right)\) với mọi \(m\) khi \(\left( {x;y} \right)\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}{x^2} - 1 = 0\\y - {x^3} + 4{x^2} + 4x = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = \pm 1\\y = {x^3} - 4{x^2} - 4x\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 1,y = - 7\\x = - 1;y = - 1\end{array} \right.\)
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm \(\left( {1; - 7} \right)\) và \(\left( { - 1; - 1} \right).\)
b)
Ta có: \(y' = 3{x^2} - 2(m + 4)x - 4\); \(\Delta ' = {(m + 4)^2} + 12 > 0,\forall m\)
Do dó phương trình \(y' = 0\) luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó).
Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
c)
Với \(m = 0\) ta được hàm số \(y = {x^3} - 4{x^2} - 4x\).
TXĐ: \(D = \mathbb{R}\)
Chiều biến thiên:
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \)
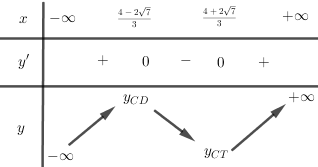
Có \(y' = 3{x^2} - 8x - 4\), \(y' = 0 \Leftrightarrow x = \dfrac{{4 \pm 2\sqrt 7 }}{3}\)
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;\frac{{4 - 2\sqrt 7 }}{3}} \right)\) và \(\left( {\frac{{4 + 2\sqrt 7 }}{3}; + \infty } \right)\)
Hàm số nghịch biến trên khoảng \(\left( {\frac{{4 - 2\sqrt 7 }}{3};\frac{{4 + 2\sqrt 7 }}{3}} \right)\)
Hàm số đạt cực đại tại \(x = \frac{{4 - 2\sqrt 7 }}{3}\), đạt cực tiểu tại \(x = \frac{{4 + 2\sqrt 7 }}{3}\)
Bảng biến thiên:
Đồ thị
d)
Với \(m = 0\) ta có:\(y = {x^3}-4{x^2}-4x\).
Xét phương trình hoành độ giao điểm: \({x^3}-4{x^2}-4x = kx\) (2)
Đường thẳng \(y = kx\) cắt (C) tại ba điểm phân biệt nếu phương trình (2) có ba nghiệm phân biệt.
Có
\(\begin{array}{l}
\left( 2 \right) \Leftrightarrow {x^3} - 4{x^2} - 4x - kx = 0\\
\Leftrightarrow {x^3} - 4{x^2} - \left( {k + 4} \right)x = 0
\end{array}\) \( \Leftrightarrow x\left[ {{x^2} - 4x - \left( {k + 4} \right)} \right] = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 4x - \left( {k + 4} \right) = 0\,\,\left( 3 \right)\end{array} \right.\)
\(\left( 2 \right)\) có ba nghiệm phân biệt \( \Leftrightarrow \left( 3 \right)\) có hai nghiệm phân biệt khác \(0\)
\( \Leftrightarrow \left\{ \begin{array}{l}
\Delta ' = 4 + k + 4 > 0\\
{0^2} - 4.0 - \left( {k + 4} \right) \ne 0
\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} k + 8 > 0\\-k -4\ne 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}k > - 8\\k \ne - 4\end{array} \right.\).
Vậy với \(k > - 8\) và \(k \ne - 4\) thì \(\left( C \right)\) cắt đường thẳng \(y = kx\) tại ba điểm phân biệt.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 1.61 trang 36 SBT Toán 12
Bài tập 1.62 trang 37 SBT Toán 12
Bài tập 1.64 trang 37 SBT Toán 12
Bài tập 1.65 trang 37 SBT Toán 12
Bài tập 1.66 trang 38 SBT Toán 12
Bài tập 1.67 trang 38 SBT Toán 12
Bài tập 1.68 trang 38 SBT Toán 12
Bài tập 1.69 trang 38 SBT Toán 12
Bài tập 1.70 trang 38 SBT Toán 12
Bài tập 1.71 trang 39 SBT Toán 12
Bài tập 1.72 trang 39 SBT Toán 12
Bài tập 1.73 trang 39 SBT Toán 12
Bài tập 1.74 trang 39 SBT Toán 12
Bài tập 29 trang 27 SGK Toán 12 NC
Bài tập 30 trang 27 SGK Toán 12 NC
Bài tập 31 trang 27 SGK Toán 12 NC
Bài tập 32 trang 28 SGK Toán 12 NC
Bài tập 33 trang 28 SGK Toán 12 NC
Bài tập 40 trang 43 SGK Toán 12 NC
Bài tập 41 trang 44 SGK Toán 12 NC
Bài tập 42 trang 45 SGK Toán 12 NC
Bài tập 43 trang 44 SGK Toán 12 NC
Bài tập 44 trang 44 SGK Toán 12 NC
Bài tập 45 trang 44 SGK Toán 12 NC
Bài tập 46 trang 44 SGK Toán 12 NC
Bài tập 47 trang 45 SGK Toán 12 NC
Bài tập 48 trang 45 SGK Toán 12 NC
Bài tập 49 trang 49 SGK Toán 12 NC
Bài tập 50 trang 49 SGK Toán 12 NC
Bài tập 51 trang 49 SGK Toán 12 NC
Bài tập 52 trang 50 SGK Toán 12 NC
Bài tập 53 trang 50 SGK Toán 12 NC
Bài tập 54 trang 50 SGK Toán 12 NC
Bài tập 55 trang 50 SGK Toán 12 NC
Bài tập 56 trang 50 SGK Toán 12 NC
Bài tập 57 trang 55 SGK Toán 12 NC
Bài tập 58 trang 56 SGK Toán 12 NC
Bài tập 59 trang 56 SGK Toán 12 NC
Bài tập 60 trang 56 SGK Toán 12 NC
Bài tập 61 trang 56 SGK Toán 12 NC
Bài tập 62 trang 57 SGK Toán 12 NC
Bài tập 63 trang 57 SGK Toán 12 NC
Bài tập 64 trang 57 SGK Toán 12 NC
-


Tìm m để đường thẳng y=-x cắt đồ thị y= x^3-6x^2 9mx tại 3 điểm phân biệt ?
bởi Le Phuong Thao
 10/09/2020
10/09/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để hàm số y=m/3x^3-(m-1)x^2 3(m-2)x 1/3 đồng biến trên (2;+vô cực).
bởi Nhoc's Quậy
 05/09/2020
Hàm số y=m/3x^3 - (m-1)x^2 3(m-2)x 1/2
05/09/2020
Hàm số y=m/3x^3 - (m-1)x^2 3(m-2)x 1/2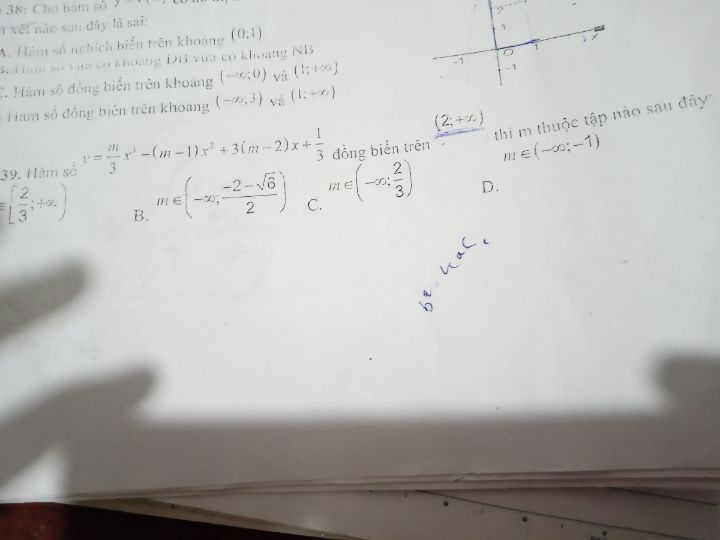 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để phương trình \(\left| {{x^4} - 4{x^2} + 3} \right| + 2m - 1 = 0\) có 8 nghiệm phân biệt?
bởi Trần Nhậm
 09/08/2020
09/08/2020
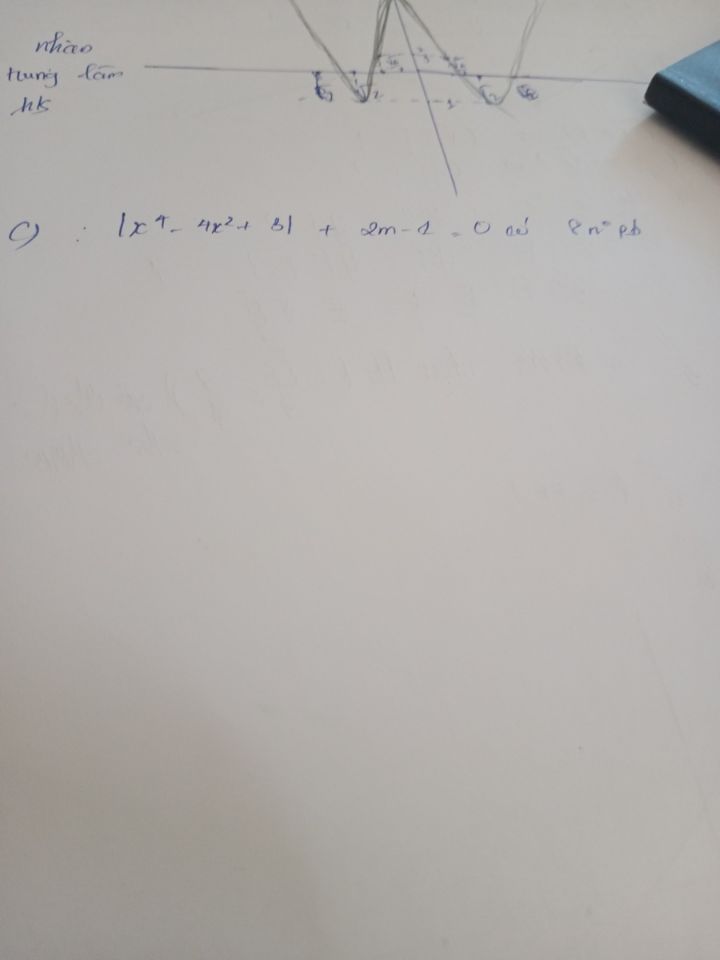 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -
ADMICRO


Tính diện tích S của tam giác OAB?
bởi Linh Lê Thị
 28/07/2020
28/07/2020
Biết đồ thị hàm số y= (x-2)(x+1) cắt trục Ox, Oy lần lượt tại hai điểm phân biệt A, B. Tính diện tích S của tam giác OAB
Theo dõi (0) 5 Trả lời -


Có bao nhiêu tiếp tuyến?
bởi vũ thị huyền nhung
 19/07/2020
19/07/2020
giúp em với ạ !!
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tim m để hàm số có 2 cực trị?
bởi lê sỹ hùng
 04/07/2020
Tim m để hàm số có 2 cực trị
04/07/2020
Tim m để hàm số có 2 cực trị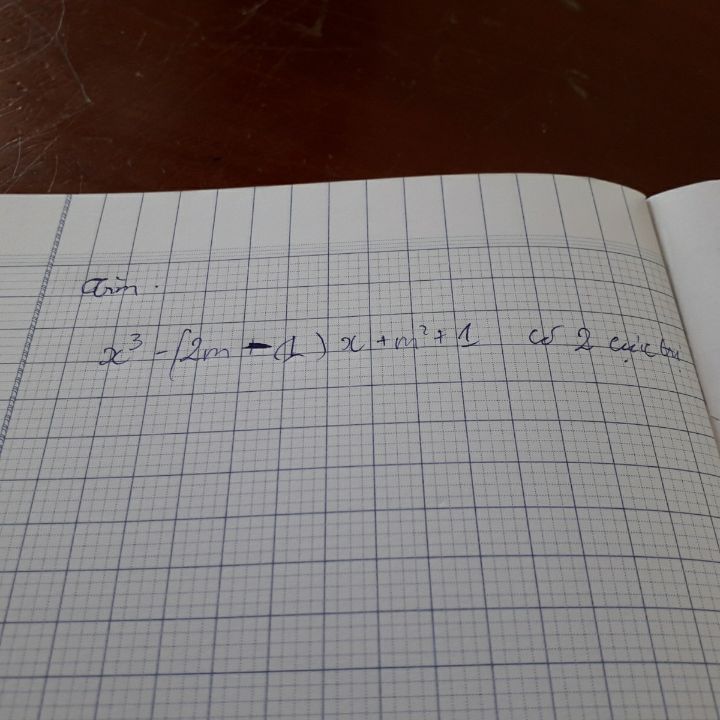 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời





