Giải bài 5 tr 99 sách GK Toán Hình lớp 12
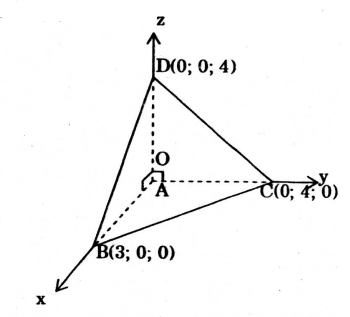
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC). Biết rằng AC = AD = 4cm, AB = 3cm, BC = 5 cm.
a) Tính thể tích tứ diện ABCD.
b) Tính khoảng cách từ điểm A tới mặt phẳng (BCD).
Hướng dẫn giải chi tiết bài 5
Câu a:
Chọn hệ toạ độ gốc là điểm \(A\), các đường thẳng \(AB, AC, AD\) theo thứ tự là các trục \(Ox, Oy, Oz\).
Ta có: \(A(0; 0; 0), B(3; 0; 0);C(0; 4; 0), D(0; 0; 4)\)
Ta có: \(\overrightarrow {AB} = (3; 0; 0) \Rightarrow AB = 3\)
\(\overrightarrow {AC} = (0; 4; 0) \Rightarrow AC = 4\)
\(\overrightarrow {AD} = (0; 0; 4) \Rightarrow AD = 4\)
\(V_{ABCD}\) = \({1 \over 6}AB.AC.AD = 8 (cm^3)\)
Câu b:
Áp dụng công thức phương trình mặt phẳng theo đoạn chắn, ta có phương trình mặt phẳng \((BDC)\) là:
\({x \over 3} + {y \over 4} + {z \over 4} = 1 \Leftrightarrow 4x + 3y + 3z - 12 = 0\)
Từ đây ta có: \(d(A, (BDC)) ={{\left| {12} \right|} \over {\sqrt {{4^2} + {3^2} + {3^2}} }} = {{12} \over {\sqrt {34} }}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3 trang 99 SGK Hình học 12
Bài tập 4 trang 99 SGK Hình học 12
Bài tập 6 trang 100 SGK Hình học 12
Bài tập 7 trang 100 SGK Hình học 12
Bài tập 8 trang 100 SGK Hình học 12
Bài tập 9 trang 100 SGK Hình học 12
Bài tập 10 trang 100 SGK Hình học 12
Bài tập 11 trang 101 SGK Hình học 12
Bài tập 12 trang 101 SGK Hình học 12
Bài tập 13 trang 101 SGK Hình học 12
Bài tập 14 trang 101 SGK Hình học 12
Bài tập 15 trang 101 SGK Hình học 12
Bài tập 16 trang 102 SGK Hình học 12
Bài tập 1 trang 122 SGK Hình học 12 NC
Bài tập 2 trang 122 SGK Hình học 12 NC
Bài tập 3 trang 122 SGK Hình học 12 NC
Bài tập 4 trang 122 SGK Hình học 12 NC
Bài tập 5 trang 122 SGK Hình học 12 NC
Bài tập 6 trang 123 SGK Hình học 12 NC
Bài tập 7 trang 123 SGK Hình học 12 NC
Bài tập 8 trang 123 SGK Hình học 12 NC
Bài tập 9 trang 123 SGK Hình học 12 NC
Bài tập 10 trang 123 SGK Hình học 12 NC
Bài tập 1 trang 127 SGK Hình học 12 NC
Bài tập 2 trang 127 SGK Hình học 12 NC
Bài tập 3 trang 127 SGK Hình học 12 NC
Bài tập 4 trang 128 SGK Hình học 12 NC
Bài tập 5 trang 128 SGK Hình học 12 NC
Bài tập 6 trang 128 SGK Hình học 12 NC
Bài tập 7 trang 128 SGK Hình học 12 NC
Bài tập 8 trang 129 SGK Hình học 12 NC
Bài tập 9 trang 129 SGK Hình học 12 NC
Bài tập 10 trang 129 SGK Hình học 12 NC
Bài tập 12 trang 129 SGK Hình học 12 NC
Bài tập 11 trang 129 SGK Hình học 12 NC
Bài tập 13 trang 129 SGK Hình học 12 NC
Bài tập 14 trang 130 SGK Hình học 12 NC
Bài tập 15 trang 130 SGK Hình học 12 NC
Bài tập 16 trang 130 SGK Hình học 12 NC
Bài tập 17 trang 130 SGK Hình học 12 NC
Bài tập 18 trang 130 SGK Hình học 12 NC
Bài tập 19 trang 131 SGK Hình học 12 NC
Bài tập 21 trang 131 SGK Hình học 12 NC
Bài tập 22 trang 131 SGK Hình học 12 NC
Bài tập 23 trang 132 SGK Hình học 12 NC
Bài tập 1 trang 168 SBT Hình học Toán 12
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 4 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


Cho hình chóp S.ABC có \(SA = \dfrac{{a\sqrt 3 }}{2}\), các cạnh còn lại cùng bằng a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC.
bởi Ngoc Son
 08/05/2022
Theo dõi (0) 1 Trả lời
08/05/2022
Theo dõi (0) 1 Trả lời -


Cho hình lăng trụ ABC.A’B’C’ có thể tích là \(V\). Điểm M nằm trên cạnh AA’ sao cho AM = 2MA’. Gọi \(V'\) là thể tích của khối chóp M.BCC’B’. Hãy tính tỉ số \(\dfrac{{V'}}{V}\).
bởi Mai Linh
 09/05/2022
Theo dõi (0) 1 Trả lời
09/05/2022
Theo dõi (0) 1 Trả lời -


Cho đường tròn \((T):{(x - 1)^2} + {(y + 2)^2} = 5\) và hai điểm A(3; -1), B(6; -2). Hãy viết phương trình đường thẳng cắt (T) tại hai điểm C, D sao cho ABCD là hình bình hành.
bởi Trinh Hung
 08/05/2022
Theo dõi (0) 1 Trả lời
08/05/2022
Theo dõi (0) 1 Trả lời -


Trong không gian với hệ tọa độ Oxyz viết phương trình đường thẳng giao tuyến của hai mặt phẳng sau \((\alpha ):x + 3y - z + 1 = 0,\)\((\beta ):2x - y + z - 7 = 0\) .
bởi Thuy Kim
 09/05/2022
Theo dõi (0) 1 Trả lời
09/05/2022
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho biết hình trụ có diện tích xung quanh bằng \(50\pi \) và độ dài đường sinh bằng đường kính của đường tròn đáy. Tính bán kính r của đường tròn đáy.
bởi Nguyễn Trung Thành
 08/05/2022
Theo dõi (0) 1 Trả lời
08/05/2022
Theo dõi (0) 1 Trả lời -


Trong không gian với hệ tọa độ Oxyz, hãy viết phương trình mặt phẳng tiếp xúc với mặt cầu \({(x - 1)^2} + {y^2} + {(z + 2)^2} = 6\) đồng thời song song với hai đường thẳng \({d_1}:\dfrac{{x - 2}}{3} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{z}{{ - 1}},{d_2}:\dfrac{x}{1} = \dfrac{{y + 2}}{1} = \dfrac{{z - 2}}{{ - 1}}\) .
bởi Van Tho
 09/05/2022
Theo dõi (0) 1 Trả lời
09/05/2022
Theo dõi (0) 1 Trả lời -


Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB = a, \(AD = a\sqrt 3 \), SA vuông góc với đáy và mặt phẳng (SBC) tạo với đáy một góc \(60^o\). Hãy tính thể tích V của khối chóp S.ABCD.
bởi Nguyễn Trà Long
 08/05/2022
Theo dõi (0) 1 Trả lời
08/05/2022
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a; (SAD) ^ (ABCD), tam giác SAD đều. Tính góc giữa BC và SA
bởi Lan Anh
 08/05/2022
Theo dõi (0) 1 Trả lời
08/05/2022
Theo dõi (0) 1 Trả lời -


Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng \({d_1}:\dfrac{{x - 1}}{2} = \dfrac{y}{1} = \dfrac{{z + 2}}{{ - 2}},\) \({d_2}:\dfrac{{x + 2}}{{ - 2}} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{z}{2}\). Hãy xét vị trí tương đối của hai đường thẳng đã cho.
bởi Anh Trần
 09/05/2022
Theo dõi (0) 1 Trả lời
09/05/2022
Theo dõi (0) 1 Trả lời -


Cho hình phẳng giới hạn bởi các đường \(y = \tan x,\,y = 0,\,\,x = 0,{\rm{ }}x = \dfrac{\pi }{4}\) quay xung quanh trục Ox. Tính thể tích của khối tròn xoay tạo thành.
bởi Huong Giang
 08/05/2022
Theo dõi (0) 1 Trả lời
08/05/2022
Theo dõi (0) 1 Trả lời -


Trong không gian với hệ tọa độ Oxyz cho đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 1 - t}\\{y = 2 + 2t}\\{z = 3 + t}\end{array}} \right.\) và mặt phẳng (P):\(x - y + 3 = 0\). Hãy tính số đo góc giữa đường thẳng d và mặt phẳng (P).
bởi Lê Trung Phuong
 09/05/2022
Theo dõi (0) 1 Trả lời
09/05/2022
Theo dõi (0) 1 Trả lời -


Trong không gian với hệ tọa độ \(Oxyz\) cho ba đường thẳng \({d_1}:\left\{ \begin{array}{l}x = t\\y = 4 - t\\z = - 1 + 2t\end{array} \right.\), \({d_2}:\frac{x}{1} = \frac{{y - 2}}{{ - 3}} = \frac{z}{{ - 3}}\) và \({d_3}:\frac{{x + 1}}{5} = \frac{{y - 1}}{2} = \frac{{z + 1}}{1}.\) Gọi \(\Delta \) là đường thẳng cắt \({d_1},{d_2},{d_3}\) lần lượt tại các điểm \(A,B,C\) sao cho \(AB = BC\). Viết phương trình đường thẳng \(\Delta \)
bởi Nguyễn Minh Minh
 09/05/2022
Theo dõi (0) 1 Trả lời
09/05/2022
Theo dõi (0) 1 Trả lời