Bài tập 10 trang 170 SBT Hình học Toán 12
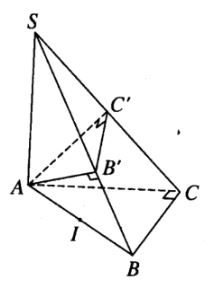
Trong không gian Oxyz, cho S(0; 0; 2), A(0; 0; 0), B(1; 2; 0), C(0; 2; 0)
a) Viết phương trình của mặt phẳng (P) qua A và vuông góc với SB;
b) Tìm tọa độ của các điểm B' là gia của (P) với đường thẳng SB, C' là giao của (P) với đường thẳng SC;
c) Tính thể tích tứ diện SAB'C';
d) Tìm điểm đối xứng với B qua mặt phẳng (P);
e) Chứng minh các điểm A, B, C, B', C' cùng thuộc một mặt cầu. Viết phương trình của mặt cầu đó và phương trình của mặt phẳng tiếp xúc với mặt cầu đó tại C'.
Hướng dẫn giải chi tiết Bài tập 10 trang 170
a) \(\overrightarrow {SB} = \left( {1;2; - 2} \right)\)
Phương trình (P) đi qua A và nhận \(\overrightarrow {SB} \) làm VTPT là:
x + 2y - 2z = 0.
b) Phương trình đường thẳng SB: \(\left\{ \begin{array}{l}x = t\\y = 2t\\z = 2 - 2t\end{array} \right.\).
Để tìm B' ta giải hệ \(\left\{ \begin{array}{l}x + 2y - 2z = 0\\x = t\\y = 2t\\z = 2 - 2t\end{array} \right.\)
\( \Rightarrow t + 2.2t - 2\left( {2 - 2t} \right) = 0\) \( \Leftrightarrow 9t - 4 = 0 \Leftrightarrow t = \frac{4}{9}\)
\( \Rightarrow B'\left( {\frac{4}{9};\frac{8}{9};\frac{{10}}{9}} \right)\)
Tương tự, C'(0; 1; 1)
c)
\(\overrightarrow {C'B'} = \left( {\frac{4}{9}; - \frac{1}{9};\frac{1}{9}} \right)\), \(\overrightarrow {AC'} = \left( {0;1;1} \right)\)
\( \Rightarrow \overrightarrow {C'B'} .\overrightarrow {AC'} = 0\) \( \Rightarrow C'B' \bot AC'\)
\( \Rightarrow {S_{AB'C'}} = \frac{1}{2}AC'.C'B'\) \( = \frac{1}{2}.\sqrt 2 .\sqrt {\frac{{16 + 1 + 1}}{{81}}} = \frac{1}{3}\)
Mà \(SB' = \sqrt {S{A^2} - AB{'^2}} \) \( = \sqrt {4 - \frac{{20}}{9}} = \frac{4}{3}\)
Vậy \({V_{S.AB'C'}} = \frac{4}{{27}}\).
d) Đường thẳng qua B và vuông góc với (P) có phương trình: \(\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 2t\\z = - 2t\end{array} \right.\)
Để tìm giao điểm Bo của đường thẳng này với (P) ta giải hệ
\(\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 2t\\z = - 2t\\x + 2y - 2z = 0\end{array} \right.\)\( \Rightarrow 1 + t + 2\left( {2 + 2t} \right) - 2\left( { - 2t} \right) = 0\) \( \Leftrightarrow 9t + 5 = 0 \Leftrightarrow t = - \frac{5}{9}\)
\( \Rightarrow {B_0}\left( {\frac{4}{9};\frac{8}{9};\frac{{10}}{9}} \right)\)
Từ đó suy ra điểm đối xứng với B qua (P) là \({B_1}\left( { - \frac{1}{9}; - \frac{2}{9};\frac{{20}}{9}} \right)\)
e) Dễ thấy \(\overrightarrow {BC} \bot \overrightarrow {AC} ,\overrightarrow {BC'} \bot \overrightarrow {AC'} ,\overrightarrow {BB'} \bot \overrightarrow {AB'} \) nên A, B, C, B', C' cùng thuộc mặt cầu tâm I(1/2; 1; 0) là trung điểm của AB, bán kính IA = (√5) /2
Phương trình mặt cầu đó là \({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = \frac{5}{4}\)
Vì điểm C' thuộc mặt cầu, nên mặt phẳng tiếp xúc với mặt cầu tại C' phải vuông góc với \(\overrightarrow {IC'} = \left( { - \frac{1}{2};0;1} \right)\)
Phương trình của mặt phẳng đó là: x - 2(z - 1) = 0 hay x - 2z + 2 = 0.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


1 hình trụ có chu vi đường tròn đáy \(8\pi a\) và đường sinh có chiều dài bằng \(3a\). Thể tích của khối trụ bằng
bởi Nguyễn Thị An
 07/06/2021
07/06/2021
A. \(48\pi {a^3}\)
B. \(16\pi {a^3}\)
C. \(12\pi {a^3}\)
D. \(32\pi {a^3}\)
Theo dõi (0) 1 Trả lời -


Cho hình nón có đỉnh \(S\) và bán kính đường tròn đáy \(R = a\sqrt 2 \), góc ở đỉnh bằng \(60^\circ \). Diện tích xung quanh của hình nón bằng đáp án?
bởi Hoàng Anh
 07/06/2021
07/06/2021
A. \(\dfrac{{4\pi {a^2}\sqrt 3 }}{3}\)
B.\(4\pi {a^2}\)
C. \(8\pi {a^2}\)
D. \(\dfrac{{8\pi {a^2}\sqrt 3 }}{3}\)
Theo dõi (0) 1 Trả lời -


Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(BC = 3a,AC = 5a,\) cạnh bên \(A'A = 6a\). Cho biết thể tích khối lăng trụ bằng đáp án?
bởi Nguyễn Thị Thúy
 08/06/2021
08/06/2021
A. \(12{a^3}\)
B. \(9{a^3}\)
C. \(36{a^3}\)
D. \(45{a^3}\)
Theo dõi (0) 1 Trả lời -


A. \(3\)
B. \(4\)
C. \(6\)
D. \(9\)
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 3a,AD = 4a\) và \(AC' = 10a\). Thể tích của khối hộp đã cho bằng đáp án?
bởi Mai Vàng
 07/06/2021
07/06/2021
A. \(48\sqrt 3 {a^3}\)
B. \(60{a^3}\)
C. \(20\sqrt 3 {a^3}\)
D. \(60\sqrt 3 {a^3}\)
Theo dõi (0) 1 Trả lời -


Kim tự tháp Kheops thời Ai Cập cổ đại vừa xây xong có hình dạng là một khối chóp tứ giác đều có cạnh đáy bằng \(231\left( m \right)\), góc giữa mặt bên và mặt đáy khoảng \(51,74^\circ \). Cho biết thể tích kim tự tháp gần với giá trị nào sau đây?
bởi Hữu Nghĩa
 08/06/2021
08/06/2021
A. \(7.815.170\left( {{m^3}} \right)\)
B. \(2.605.057\left( {{m^3}} \right)\)
C. \(3.684.107\left( {{m^3}} \right)\)
D. \(11.052.320\left( {{m^3}} \right)\)
Theo dõi (0) 1 Trả lời -


Cho một hình nón có đường kính đường tròn đáy bằng \(10cm\) và chiều dài đường sinh bằng \(15cm\). Thể tích của khối nón bằng
bởi Nguyễn Thanh Hà
 07/06/2021
07/06/2021
A. \(\dfrac{{500\pi \sqrt 5 }}{3}\left( {c{m^3}} \right)\)
B. \(\dfrac{{250\pi \sqrt 2 }}{3}\left( {c{m^3}} \right)\)
C. \(250\pi \sqrt 2 \left( {c{m^3}} \right)\)
D. \(500\pi \sqrt 5 \left( {c{m^3}} \right)\)
Theo dõi (0) 1 Trả lời -


Ta có \(l,h,R\) lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Diện tích xung quanh của hình trụ là
bởi Thu Hang
 07/06/2021
07/06/2021
A. \({S_{xq}} = \pi Rl\)
B. \({S_{xq}} = 2\pi Rl\)
C. \({S_{xq}} = \pi Rh\)
D. \({S_{xq}} = 4\pi Rl\)
Theo dõi (0) 1 Trả lời -


Gọi \(l,h,R\) lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Cho biết diện tích toàn phần \({S_{tp}}\) của hình nón là:
bởi Dương Quá
 08/06/2021
08/06/2021
A. \({S_{tp}} = \pi Rl + 2\pi {R^2}\)
B. \({S_{tp}} = 2\pi Rl + 2\pi {R^2}\)
C. \({S_{tp}} = 2\pi Rl + \pi {R^2}\)
D. \(\pi Rl + \pi {R^2}\)
Theo dõi (0) 1 Trả lời -


Cho khối chóp có đáy là hình vuông cạnh \(2a\) và chiều cao bằng \(3a\). Thể tích của khối chóp đã cho bằng bao nhiêu?
bởi Ngoc Han
 07/06/2021
07/06/2021
A. \(4{a^3}\)
B. \(12{a^3}\)
C. \({a^3}\)
D. \(3{a^3}\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp đều \(S.ABC\) có tất cả các cạnh đều bằng \(a\). Mặt phẳng \(\left( P \right)\) song song với mặt phẳng \(\left( {ABC} \right)\) và cắt các cạnh \(SA,SB,SC\) lần lượt tại \(A',B',C'\). Hãy tính diện tích của tam giác \(A'B'C'\) biết \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{1}{7}\)
bởi Ngoc Nga
 06/06/2021
06/06/2021
A. \({S_{\Delta A'B'C'}} = \dfrac{{{a^2}\sqrt 3 }}{{16}}\)
B. \({S_{\Delta A'B'C'}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
C. \({S_{\Delta A'B'C'}} = \dfrac{{{a^2}\sqrt 3 }}{8}\)
D. \({S_{\Delta A'B'C'}} = \dfrac{{{a^2}\sqrt 3 }}{{48}}\)
Theo dõi (0) 1 Trả lời -


Cho lăng trụ xiên \(ABC.A'B'C'\) có đáy \(\Delta ABC\) đều cạnh \(a\). Góc giữa cạnh bên và mặt đáy là \(60^\circ \) và \(A'A = A'B = A'C\). Hãy tính thể tích của khối lăng trụ:
bởi Thanh Nguyên
 07/06/2021
07/06/2021
A. \(V = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)
B. \(V = \dfrac{{{a^3}\sqrt 3 }}{4}\)
C. \(V = \dfrac{{{a^3}\sqrt 3 }}{2}\)
D.\(V = \dfrac{{3{a^3}\sqrt 3 }}{8}\)
Theo dõi (0) 1 Trả lời