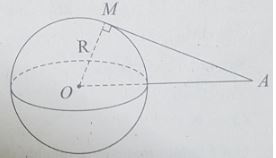
Bài tập 8 trang 171 SBT Hình học Toán 12
Cho mặt cầu S(O;R) và điểm A cố định với OA = d > R. Qua A kẻ đường thẳng Δ tiếp xúc với mặt cầu S(O;R) tại M. Độ dài đoạn thẳng AM là:
\(\begin{array}{l}
A.\sqrt {{d^2} + {R^2}} \\
B.\sqrt {2{R^2} - {d^2}} \\
C.\sqrt {{R^2} - 2{d^2}} \\
D.\sqrt {{d^2} - {R^2}}
\end{array}\)
Hướng dẫn giải chi tiết Bài tập 8 trang 171
Vì Δ tiếp xúc với S(O;R) tại M nên OM ⊥ Δ tại M.
Xét tam giác OMA vuông tại M, ta có:
AM2 = OA2 - OM2 = d2 - R2
\( \Rightarrow AM = \sqrt {{d^2} - {R^2}} \)
Chọn D.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


Trong không gian Oxyz, cho mặt cầu (S): x2 + y2 + z2 - 2x + 4y + 2z - 19 = 0 và mặt phẳng (P): x - 2y + 2z - 12 = 0. Hãy chứng minh rằng (P) cắt (S) theo một đường tròn.
bởi Bao Chau
 24/05/2021
24/05/2021
Trong không gian Oxyz, cho mặt cầu (S): x2 + y2 + z2 - 2x + 4y + 2z - 19 = 0 và mặt phẳng (P): x - 2y + 2z - 12 = 0. Chứng minh rằng (P) cắt (S) theo một đường tròn.
Theo dõi (0) 1 Trả lời -


Trong không gian Oxyz, cho mặt phẳng (P): x + 2y - z + 5 = 0 và hai điểm A(-2; -1; 1), B(6; 6; 5). Trong các đường thẳng qua A và song song với (P), hãy viết phương trình đường thẳng mà khoảng cách từ B đến đường thẳng đó là nhỏ nhất.
bởi Quynh Nhu
 24/05/2021
24/05/2021
Trong không gian Oxyz, cho mặt phẳng (P): x + 2y - z + 5 = 0 và hai điểm A(-2; -1; 1), B(6; 6; 5). Trong các đường thẳng qua A và song song với (P), hãy viết phương trình đường thẳng mà khoảng cách từ B đến đường thẳng đó là nhỏ nhất.
Theo dõi (0) 1 Trả lời -


Cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 3 + t\\y = 1 - t\\z = 2t\end{array} \right.,d':\left\{ \begin{array}{l}x = 1 + t'\\y = 2t'\\z = - 1 + t'\end{array} \right.\) và M(2; -1; 0). Tìm tọa độ điểm A trên d và điểm B trên d' để M, A, B thẳng hàng.
bởi Lê Minh Hải
 24/05/2021
24/05/2021
Cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 3 + t\\y = 1 - t\\z = 2t\end{array} \right.,d':\left\{ \begin{array}{l}x = 1 + t'\\y = 2t'\\z = - 1 + t'\end{array} \right.\) và M(2; -1; 0). Tìm tọa độ điểm A trên d và điểm B trên d' để M, A, B thẳng hàng.
Theo dõi (0) 1 Trả lời -


Cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 3 + t\\y = 1 - t\\z = 2t\end{array} \right.,d':\left\{ \begin{array}{l}x = 1 + t'\\y = 2t'\\z = - 1 + t'\end{array} \right.\) và M(2; -1; 0). Chứng minh rằng d và d' chéo nhau.
bởi Thanh Thanh
 25/05/2021
25/05/2021
Cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 3 + t\\y = 1 - t\\z = 2t\end{array} \right.,d':\left\{ \begin{array}{l}x = 1 + t'\\y = 2t'\\z = - 1 + t'\end{array} \right.\) và M(2; -1; 0). Chứng minh rằng d và d' chéo nhau.
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho ba điểm A(1; 2; 1), B(2; -1; 1), C(0; 3; 1) và đường thẳng d: \(\frac{x}{{ - 3}} = \frac{y}{{ - 1}} = \frac{z}{2}\). Viết phương trình mặt phẳng (P) đi qua A, song song với d, sao cho khoảng cách từ B đến (P) bằng khoảng cách từ C đến (P).
bởi Hoa Lan
 24/05/2021
24/05/2021
Cho ba điểm A(1; 2; 1), B(2; -1; 1), C(0; 3; 1) và đường thẳng d: \(\frac{x}{{ - 3}} = \frac{y}{{ - 1}} = \frac{z}{2}\). Viết phương trình mặt phẳng (P) đi qua A, song song với d, sao cho khoảng cách từ B đến (P) bằng khoảng cách từ C đến (P).
Theo dõi (0) 1 Trả lời -


Cho tam giác MNP vuông tại M, có MN = 3cm, MP = 4cm, tia phân giác NI của góc N( I thuộc MP). Vẽ IE vuông góc với NP tại E. Tính độ dài đoạn thẳng NP.
bởi Kazumi Nana
 12/05/2021
12/05/2021
bài 1Cho tam giác MNP vuông tại M, có MN = 3cm, MP = 4cm,
tia phân giác NI của góc N( I thuộc MP). Vẽ IE vuông góc với NP tại E.
a. Tính độ dài đoạn thẳng NP.
b. Chứng minh: tam giác MNI bằng tam giác ENI
c. Chứng minh: NI là đường trung trực của đoạn thẳng ME.
d. Gọi F là giao điểm của tia NM và EI. Chứng minh NI vuông góc với FP.
Bài 2. Cho đa thức f(x) = ax3 + bx2 +cx + d trong đó a,b,c,d là các số nguyên và thỏa mãn 7a +2b + c = 0
Chứng minh rằng f(-1).f(3) là bình phương của một số nguyên
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, biết \(AB = BC = a\), \(AD = 2a\) và SA vuông góc với mặt phẳng đáy, \(SA = a\sqrt 2 \). Tính số đo của góc \(\varphi \) là góc giữa hai mặt phẳng (SCD) và (SAD).
bởi Hoa Lan
 06/05/2021
06/05/2021
A. \(\varphi = {60^0}\)
B. \(\varphi = {45^0}\)
C. \(\varphi = {30^0}\)
D. \(\varphi = {90^0}\)
Theo dõi (0) 1 Trả lời -


Lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác cân tại C ,\(\angle BAC = 30^\circ ,\) \(AB = a\sqrt 3 ,\) \(AA' = a\). Gọi \(M\) là trung điểm của \(BB'\). Tính theo \(a\) thể tích \(V\) của khối tứ diện \(MACC'\).
bởi khanh nguyen
 07/05/2021
07/05/2021
A. \(V = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)
B. \(V = \dfrac{{{a^3}\sqrt 3 }}{4}\)
C. \(V = \dfrac{{{a^3}\sqrt 3 }}{3}\)
D. \(V = \dfrac{{{a^3}\sqrt 3 }}{{18}}\)
Theo dõi (0) 1 Trả lời -


Mặt phẳng Oxy, có bao nhiêu điểm mà từ đó kẻ được hai tiếp tuyến đến đồ thị hàm số \(y = \dfrac{{{x^3}}}{3} - \dfrac{{{x^2}}}{2} + x + 1\) sao cho hai tiếp tuyến này vuông góc với nhau?
bởi Nguyễn Thị Lưu
 06/05/2021
06/05/2021
A. 0
B. 1
C. 2
D. Vô số
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(2a\), cạnh \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = 2a\). Khi đó góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {SAC} \right)\) bằng bao nhiêu độ?
bởi trang lan
 07/05/2021
07/05/2021
.jpg)
A. \({90^0}\)
B. \({45^0}\)
C. \({60^0}\)
D. \({30^0}\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.ABCD\) có đáy là hình bình hành \(ABCD\). Gọi \(M,\,\,N\) lần lượt là trung điểm các cạnh \(SA,\,\,SB\) và \(P\) là điểm bất kỳ thuộc cạnh \(CD\). Biết thể tích khối chóp \(S.ABCD\) là \(V\). Thể tích của khối tứ diện \(AMNP\) theo \(V\). là:
bởi Cam Ngan
 07/05/2021
07/05/2021
A. \(\dfrac{V}{8}\)
B. \(\dfrac{V}{{12}}\)
C. \(\dfrac{V}{6}\)
D. \(\dfrac{V}{4}\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), mặt bên \(SAB\) nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right),\) \(\widehat {SAB} = {30^0},SA = 2a.\) Tính thể tích \(V\) của khối chóp \(S.ABCD\) được kết quả là:
bởi Nguyễn Hoài Thương
 07/05/2021
07/05/2021
A. \(V = \dfrac{{\sqrt 3 {a^3}}}{6}.\)
B. \(V = {a^3}.\)
C. \(V = \dfrac{{{a^3}}}{9}.\)
D. \(V = \dfrac{{{a^3}}}{3}.\)
Theo dõi (0) 1 Trả lời