Bài tập 20 trang 173 SBT Hình học Toán 12
Một khối trụ có chu vi đáy bằng 6π cm và thiết diện đi qua là một hình chữ nhật có độ dài đường chéo bằng 10 cm. Thể tích khối trụ là:
A. 72π (cm3) B. 24π (cm3)
C. 48π (cm3) D. 18π√(34) (cm3)
Hướng dẫn giải chi tiết Bài tập 20 trang 173
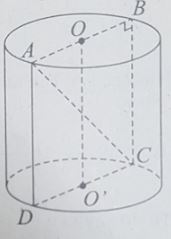
Gọi O, O' là hai tâm của hai đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.
Do chu vi đáy của hình trụ đó bằng 6π (cm) nên bán kính đáy của hình trụ là: R = 3 (cm)
Vì thiết diện đi qua trục là một hình chữ nhật ABCD có AC = 10 (cm) và AB = 2R = 6 (cm) nên chiều cao của hình trụ là:
h = OO' = BC = 8 (cm)
Vậy thể tích khối trụ là: V = πR2h = 72π (cm3)
Chọn A.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
-


Gọi M là giao điểm của đường thẳng d với mặt phẳng (P) , điểm A thuộc đường thẳng d có cao độ âm sao cho \(AM=\sqrt{3}\)
bởi thi trang
 07/02/2017
07/02/2017
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d và mặt phẳng (P) lần lượt có phương trình là \(\frac{x-1}{1}=\frac{y}{1}=\frac{x+1}{1}, x-y+2z-1=0\) . Gọi M là giao điểm của đường thẳng d với mặt phẳng (P) , điểm A thuộc đường thẳng d có cao độ âm sao cho \(AM=\sqrt{3}\) . Viết phương trình mặt cầu (S) có tâm A và tiếp xúc với mặt phẳng (P) .
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có đáy ABCD là hình vuông, gọi M là trung điểm của AB. Tam giác SAB cân và nằm trong mặt phẳng vuông góc với đáy (ABCD), biết \(SD=2a\sqrt{5}\), SC tạo với mặt đáy (ABCD) một góc \(60^{\circ}\). Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng DM và SA.
Theo dõi (0) 2 Trả lời -


Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABCD). Gọi K là điểm thuộc cạnh AB thỏa KB = 3KA. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa SB và KD.
Theo dõi (0) 1 Trả lời -


Viết phương trình mặt phẳng (P) chứa đường thẳng (d) sao cho khoảng cách từ A đến (P) đạt giá trị lớn nhất
bởi Lan Anh
 08/02/2017
08/02/2017
Cho đường thẳng (d): \(\small \left\{\begin{matrix} x=1+2t\\ y=t\\ z=2+2t \end{matrix}\right.\) và điểm A(2;5;3)
a.Tìm tọa độ hình chiếu vuông góc H của A trên đường thẳng (d )
b.Viết phương trình mặt phẳng (P) chứa đường thẳng (d) sao cho khoảng cách từ A đến (P) đạt giá trị lớn nhất.
Theo dõi (0) 2 Trả lời