Bài tập 9 trang 170 SBT Hình học Toán 12
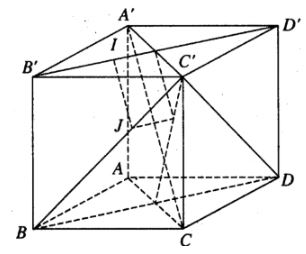
Trong không gian Oxyz cho hình lập phương ABCD.A’B’C’D’ với A(0;0;0), B(1;0;0), D(0;1;0), A’(0;0;1)
a) Hãy tìm tọa độ các đỉnh còn lại.
b) Chứng minh A'C ⊥ (BC'D)
c) Tìm tọa độ của chân đường vuông góc chung của B'D' và BC'.
Hướng dẫn giải chi tiết Bài tập 9 trang 170
a) Dễ thấy C(1; 1; 0), B'(1; 0; 1), D'(0; 1; 1), C'(1; 1; 1), D'(0; 1; 1).
b) Ta có: \(\overrightarrow {A'C} = \left( {1;1; - 1} \right)\)
\(\overrightarrow {BC'} = \left( {0;1;1} \right)\), \(\overrightarrow {BD} = \overrightarrow {B'D'} = \left( { - 1;1;0} \right)\)
Do đó \(\overrightarrow {A'C} .\overrightarrow {BC'} = 0\) và \(\overrightarrow {A'C} .\overrightarrow {BD} = 0\)
Từ đó suy ra \(A'C \bot BC',A'C \bot BD\) nên A'C ⊥ (BC'D).
c)
Gọi IJ là đường vuông góc chung của B'D' và BC'
\(\overrightarrow {{n_1}} \) là vectơ pháp tuyến của mặt phẳng (P) qua B'D' và song song với A’C
\(\overrightarrow {{n_2}} \) là vectơ pháp tuyến của mặt phẳng (Q) qua BC' và song song với A'C.
Khi đó \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {A'C} ,\overrightarrow {B'D'} } \right] = \left( {1;1;2} \right)\)
\(\overrightarrow {{n_2}} = \left[ {\overrightarrow {A'C} ,\overrightarrow {BC'} } \right] = \left( {2; - 1;1} \right)\)
Phương trình của (P) là: (x - 1) + y + 2(z - 1) = 0 hay x + y + 2z - 3 = 0.
Phương trình của (Q) là: 2(x - 1) - y + z = 0 hay 2x - y + z - 2 = 0.
Phương trình của (B'D') là: \(\left\{ \begin{array}{l}x = 1 - t\\y = t\\z = 1\end{array} \right.\) .
Phương trình của (BC') là: \(\left\{ \begin{array}{l}x = 1\\y = t\\z = t\end{array} \right.\)
I là giao điểm của đường thẳng B'D' và (Q), để tìm tọa độ của I ta thế phương trình đường thẳng B'D' vào phương trình của (Q)
Ta có: 2(1 - t) - t + 1 - 2 = 0, hay t = 1/3.
Từ đó suy ra I(2/3; 1/3; 1)
Tương tự, ta tìm được J(1; 2/3; 1/3).
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-
Khối chóp tứ giác đều \(S.ABCD\)có cạnh đáy bằng \(\sqrt 2 a\) và tam giác \(SAC\)đều. Thể tích của khối chóp đã cho bằng
bởi Nguyễn Anh Hưng
07/06/2021
A. \(\dfrac{{\sqrt 3 {a^3}}}{2}\).
B. \(\dfrac{{\sqrt 3 {a^3}}}{3}\).
C. \(\dfrac{{2\sqrt 3 {a^3}}}{3}\).
D. \(\dfrac{{3\sqrt 3 {a^3}}}{2}\).
Theo dõi (0) 1 Trả lời -
Hình nón có đường cao \(20\left( {cm} \right)\), bán kính đáy \(25\left( {cm} \right)\). Một mặt phẳng \(\left( P \right)\) qua đỉnh của hình nón và có khoảng cách đến tâm của hình tròn đáy là \(12\left( {cm} \right)\). Diện tích thiết diện tạo bởi \(\left( P \right)\) và hình nón bằng đáp án?
bởi thúy ngọc
07/06/2021
A. \(500\left( {c{m^2}} \right)\)
B. \(600\left( {c{m^2}} \right)\)
C. \(550\left( {c{m^2}} \right)\)
D. \(450\left( {c{m^2}} \right)\)
Theo dõi (0) 1 Trả lời -
Có bao nhiêu giá trị nguyên của \(m\) để hàm số sau \(y = \left| {\dfrac{3}{4}{x^4} - {x^3} - 3{x^2} + m + 2} \right|\) có 7 điểm cực trị?
bởi Mai Hoa
08/06/2021
A. \(2\)
B. \(0\)
C. \(3\)
D. \(1\)
Theo dõi (0) 1 Trả lời -
Hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\) với \(BC = 2a,\widehat {BAC} = 120^\circ \), biết \(SA \bot \left( {ABC} \right)\) và \(\left( {SBC} \right)\) hợp với đáy một góc \(45^\circ \). Tính thể tích khối chóp \(S.ABC\)
bởi Phan Thị Trinh
07/06/2021
A. \({a^3}\sqrt 2 \)
B. \(\dfrac{{{a^3}}}{2}\)
C. \(\dfrac{{{a^3}}}{3}\)
D. \(\dfrac{{{a^3}}}{9}\)
Theo dõi (0) 1 Trả lời -
ADMICRO
Với lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(2a\). Hình chiếu vuông góc của \(A'\) trên \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\), góc giữa \(A'A\) và mặt đáy bằng \(60^\circ \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
bởi Goc pho
08/06/2021
A. \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
B. \(\dfrac{{2\sqrt 3 {a^3}}}{3}\)
C. \(\sqrt 3 {a^3}\)
D. \(2\sqrt 3 {a^3}\)
Theo dõi (0) 1 Trả lời -
Với lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(2a\). Hình chiếu vuông góc của \(A'\) trên \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\), góc giữa \(A'A\) và mặt đáy bằng \(60^\circ \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
bởi Goc pho
08/06/2021
A. \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
B. \(\dfrac{{2\sqrt 3 {a^3}}}{3}\)
C. \(\sqrt 3 {a^3}\)
D. \(2\sqrt 3 {a^3}\)
Theo dõi (0) 1 Trả lời -
Với lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(2a\). Hình chiếu vuông góc của \(A'\) trên \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\), góc giữa \(A'A\) và mặt đáy bằng \(60^\circ \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
bởi Goc pho
07/06/2021
A. \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
B. \(\dfrac{{2\sqrt 3 {a^3}}}{3}\)
C. \(\sqrt 3 {a^3}\)
D. \(2\sqrt 3 {a^3}\)
Theo dõi (0) 1 Trả lời -
Với lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(2a\). Hình chiếu vuông góc của \(A'\) trên \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\), góc giữa \(A'A\) và mặt đáy bằng \(60^\circ \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
bởi Goc pho
08/06/2021
A. \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
B. \(\dfrac{{2\sqrt 3 {a^3}}}{3}\)
C. \(\sqrt 3 {a^3}\)
D. \(2\sqrt 3 {a^3}\)
Theo dõi (0) 1 Trả lời -
Với lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(2a\). Hình chiếu vuông góc của \(A'\) trên \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\), góc giữa \(A'A\) và mặt đáy bằng \(60^\circ \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
bởi Goc pho
08/06/2021
A. \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
B. \(\dfrac{{2\sqrt 3 {a^3}}}{3}\)
C. \(\sqrt 3 {a^3}\)
D. \(2\sqrt 3 {a^3}\)
Theo dõi (0) 1 Trả lời -
Với lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(2a\). Hình chiếu vuông góc của \(A'\) trên \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\), góc giữa \(A'A\) và mặt đáy bằng \(60^\circ \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
bởi Goc pho
08/06/2021
A. \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
B. \(\dfrac{{2\sqrt 3 {a^3}}}{3}\)
C. \(\sqrt 3 {a^3}\)
D. \(2\sqrt 3 {a^3}\)
Theo dõi (0) 1 Trả lời -
Với lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(2a\). Hình chiếu vuông góc của \(A'\) trên \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\), góc giữa \(A'A\) và mặt đáy bằng \(60^\circ \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
bởi Goc pho
08/06/2021
A. \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
B. \(\dfrac{{2\sqrt 3 {a^3}}}{3}\)
C. \(\sqrt 3 {a^3}\)
D. \(2\sqrt 3 {a^3}\)
Theo dõi (0) 1 Trả lời -
Với lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(2a\). Hình chiếu vuông góc của \(A'\) trên \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\), góc giữa \(A'A\) và mặt đáy bằng \(60^\circ \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
bởi Goc pho
08/06/2021
A. \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
B. \(\dfrac{{2\sqrt 3 {a^3}}}{3}\)
C. \(\sqrt 3 {a^3}\)
D. \(2\sqrt 3 {a^3}\)
Theo dõi (0) 1 Trả lời
