Bài tập 5 trang 122 SGK Hình học 12 NC
Cho hình vuông ABCD nội tiếp đường tròn (O; R). Gọi H là hình gồm các điểm của hình tròn (O; R) nhưng không nằm trong hình vuông. Tính thể tích hình tròn xoay sinh bởi hình H khi quay quanh đường thẳng chứa một đường chéo của hình vuông.
Hướng dẫn giải chi tiết
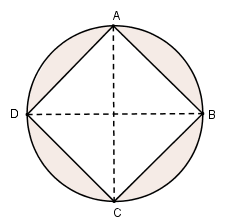
Khi quay quanh đường chéo AC thì hình tròn (O, R) sinh ra khối cầu (S), đoạn thẳng BD sinh ra hình tròn (C) và hình vuông ABCD sinh ra hình tròn xoay K gồm hai hình nón có chung đáy là (C) với đỉnh là A và C. Do đó H sinh ra khối tròn xoay gồm những điểm thuộc hình cầu (S) nhưng không thuộc K và thể tích V của khối đó là:
\(\begin{array}{l}
V = {V_{\left( S \right)}} - {V_{\left( K \right)}}\\
= \frac{4}{3}\pi {R^3} - 2.\frac{1}{3}\pi {R^2}.R = \frac{2}{3}\pi {R^3}.
\end{array}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3 trang 122 SGK Hình học 12 NC
Bài tập 4 trang 122 SGK Hình học 12 NC
Bài tập 6 trang 123 SGK Hình học 12 NC
Bài tập 7 trang 123 SGK Hình học 12 NC
Bài tập 8 trang 123 SGK Hình học 12 NC
Bài tập 9 trang 123 SGK Hình học 12 NC
Bài tập 10 trang 123 SGK Hình học 12 NC
Bài tập 1 trang 127 SGK Hình học 12 NC
Bài tập 2 trang 127 SGK Hình học 12 NC
Bài tập 3 trang 127 SGK Hình học 12 NC
Bài tập 4 trang 128 SGK Hình học 12 NC
Bài tập 5 trang 128 SGK Hình học 12 NC
Bài tập 6 trang 128 SGK Hình học 12 NC
Bài tập 7 trang 128 SGK Hình học 12 NC
Bài tập 8 trang 129 SGK Hình học 12 NC
Bài tập 9 trang 129 SGK Hình học 12 NC
Bài tập 10 trang 129 SGK Hình học 12 NC
Bài tập 12 trang 129 SGK Hình học 12 NC
Bài tập 11 trang 129 SGK Hình học 12 NC
Bài tập 13 trang 129 SGK Hình học 12 NC
Bài tập 14 trang 130 SGK Hình học 12 NC
Bài tập 15 trang 130 SGK Hình học 12 NC
Bài tập 16 trang 130 SGK Hình học 12 NC
Bài tập 17 trang 130 SGK Hình học 12 NC
Bài tập 18 trang 130 SGK Hình học 12 NC
Bài tập 19 trang 131 SGK Hình học 12 NC
Bài tập 21 trang 131 SGK Hình học 12 NC
Bài tập 22 trang 131 SGK Hình học 12 NC
Bài tập 23 trang 132 SGK Hình học 12 NC
Bài tập 1 trang 168 SBT Hình học Toán 12
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 4 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


Cho ba điểm \(A\left( {2;1; - 1} \right),\)\(B\left( { - 1;0;4} \right),\)\(C\left( {0; - 2; - 1} \right)\). Mặt phẳng đi qua \(A\) và vuông góc với BC có phương trình là đáp án
bởi sap sua
 11/06/2021
11/06/2021
A. \(x - 2y - 5z + 5 = 0\)
B. \(x - 2y - 5z - 5 = 0\)
C. \(2x - y + 5z + 5 = 0\)
D. \(x - 2y - 5z = 0\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy, \(AB = a;\,\,AD = a\sqrt 3 \). Thể tích khối chóp S.ABCD là bằng
bởi Nguyễn Hoài Thương
 11/06/2021
11/06/2021
A. \(\dfrac{{3{a^2}}}{2}.\) B. \({a^3}\)
C. \(\dfrac{{{a^3}}}{6}.\) D. \(\dfrac{{{a^3}}}{2}\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng \(\sqrt 2 a\). Tam giác SAD cân tại \(S\) và mặt bên \(\left( {SAD} \right)\) vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng \(\dfrac{4}{3}{a^3}\). Tính khoảng cách h từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\).
bởi Thanh Truc
 11/06/2021
11/06/2021
A. \(h = \dfrac{2}{3}a\) B. \(h = \dfrac{4}{3}a\)
C. \(h = \dfrac{8}{3}a\) D. \(h = \dfrac{3}{4}a\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Biết \(AC = 2a,{\mkern 1mu} {\mkern 1mu} BD = 4a\). Tính theo \(a\) khoảng cách giữa hai đường thẳng AD và SC.
bởi Hong Van
 11/06/2021
11/06/2021
A. \(\dfrac{{a\sqrt {15} }}{2}\). B. \(\dfrac{{2a\sqrt 5 }}{5}\).
C. \(\dfrac{{2{a^3}\sqrt {15} }}{3}\). D. \(\dfrac{{4a\sqrt {1365} }}{{91}}\).
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho tứ diện đều ABCD có cạnh bằng 4. Hình trụ \(\left( T \right)\) có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD. Diện tích xung quanh của \(\left( T \right)\) bằng:
bởi Lê Gia Bảo
 10/06/2021
10/06/2021
A. \(\dfrac{{16\sqrt 2 \pi }}{3}.\) B. \(8\sqrt 2 \pi .\)
C. \(\dfrac{{16\sqrt 3 \pi }}{3}.\) D. \(8\sqrt 3 \pi .\)
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm của hàm số \(f(x) = 3{x^2} + 8\sin x\).
bởi Mai Thuy
 11/06/2021
11/06/2021
A. \(\int {f\left( x \right){\rm{d}}x} {\rm{\;}} = 6x - 8\cos x + C\).
B. \(\int {f\left( x \right){\rm{d}}x} {\rm{\;}} = 6x + 8\cos x + C\).
C. \(\int {f\left( x \right){\rm{d}}x} {\rm{\;}} = {x^3} - 8\cos x + C\).
D. \(\int {f\left( x \right){\rm{d}}x} {\rm{\;}} = {x^3} + 8\cos x + C\).
Theo dõi (0) 1 Trả lời -


Trong không gian Oxyz, cho \(A\left( {1;1; - 1} \right),B\left( { - 1;2;0} \right),C\left( {3; - 1; - 2} \right)\). Giả sử \(M\left( {a;b;c} \right)\) thuộc mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {y^2} + {\left( {z + 1} \right)^2} = 861\) sao cho \(P = 2M{A^2} - 7M{B^2} + 4M{C^2}\) đạt giá trị nhỏ nhất. Giá trị \(T = \left| a \right| + \left| b \right| + \left| c \right|\) bằng câu?
bởi Tran Chau
 10/06/2021
10/06/2021
A. \(T = 47\). B. \(T = 55\)
C. \(T = 51\) D. \(T = 49\).
Theo dõi (0) 1 Trả lời -


Trong không gian \({\rm{Ox}}yz\), cho mặt cầu \((S)\) có tâm là gốc tọa độ và bán kính bằng 1. Viết phương trình mặt phẳng \((P)\) đi qua điểm \(A\left( {0;\dfrac{{\sqrt 3 }}{2};\dfrac{1}{2}} \right)\) và tiếp xúc với mặt cầu \((S)\)
bởi Bảo Hân
 11/06/2021
11/06/2021
A. \(x + \sqrt 3 y + z - 2 = 0\)
B. \(\sqrt 3 y + z - 2 = 0\)
C. \(\sqrt 3 y + 4z - 2 = 0\)
D. \(y + \sqrt 3 z - 2 = 0\)
Theo dõi (0) 1 Trả lời -


Trong mặt phẳng \(Oxy\) cho nửa đường tròn tâm \(O\). Parabol có đỉnh trùng với tâm \(O\)(trục đối xứng là trục tung) cắt nửa đường tròn tại hai điểm \(A,B\) như hình vẽ. Cho biết diện tích hình phẳng giới hạn bởi nửa đường tròn và Parabol ( phần gạch sọc)
bởi Thùy Trang
 11/06/2021
11/06/2021
.jpg)
A. \(S = \dfrac{{20}}{3} - 2\pi \)
B. \(S = \dfrac{4}{3} - 2\pi \)
C. \(S = \dfrac{{20}}{3} + 2\pi \)
D. \(S = \dfrac{4}{3} + 2\pi \)
Theo dõi (0) 1 Trả lời -


Hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\sqrt 2 \), cạnh bên hợp với mặt đáy một góc \({60^o}\). Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD\)
bởi Lê Vinh
 11/06/2021
11/06/2021
A. \(\dfrac{{2\sqrt 3 a}}{3}\)
B. \(\dfrac{{\sqrt 3 a}}{3}\)
C. \(\sqrt 3 a\)
D. \(\dfrac{{2a}}{3}\)
Theo dõi (0) 1 Trả lời -


Có hai số dương \(a,b\) thỏa mãn \(\left\{ \begin{array}{l}{\log _4}a + {\log _2}{b^2} = 3\\{\log _4}{a^2} + {\log _2}b = 9\end{array} \right.\). Hãy tính \(a + 2b\)
bởi Ánh tuyết
 11/06/2021
11/06/2021
A. \(a + 2b = 2\)
B. \(a + 2b = {2^{10}} + 1\)
C. \(a + 2b = {2^{10}}\)
D. \(a + 2b = {2^9}\)
Theo dõi (0) 1 Trả lời -


Trong không gian \(Oxyz\), cho mặt cầu \((S):{x^2} + {y^2} + {z^2} - 2x - 2y - 6z + 7 = 0.\) Biết ba điểm \(A,B,M\) nằm trên mặt cầu \((S)\) sao cho \(\widehat {AMB} = {90^o}\). Khi đó diện tích tam giác \(AMB\) có giá trị lớn nhất là bằng
bởi Hoai Hoai
 11/06/2021
11/06/2021
A. \(2\pi \) B. \(4\pi \) C. 2 D. 4
Theo dõi (0) 1 Trả lời



