Bài tập 3 trang 127 SGK Hình học 12 NC
Cho khối lăng trụ tam giác ABC.A’B’C’, M là trung điểm của cạnh AB. Trong các đẳng thức sau đây, đẳng thức nào sai ?
(A) \({V_{A'B'C'C}} = {V_{MA'B'C'}}\)
(B) \({V_{ABCC'}} = {V_{A'BCC'}}\)
(C) \({V_{MA'B'C'}} = {V_{A'ABC}}\)
(D) \({V_{MA\prime B\prime C\prime }} = \frac{1}{2}{V_{AA\prime B\prime C\prime }}\)
Hướng dẫn giải chi tiết
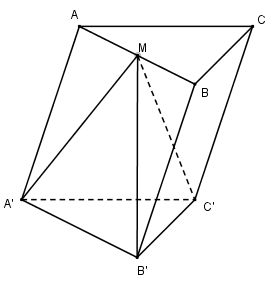
Ta có: AM // (A’B’C’)
\( \Rightarrow d\left( {A;\left( {A'B'C'} \right)} \right) = d\left( {M;\left( {A'B'C'} \right)} \right)\)
\(\begin{array}{l}
{V_{MA\prime B\prime C\prime }} = \frac{1}{3}d(M;(A\prime B\prime C\prime )).{S_{A\prime B\prime C\prime }}\\
{V_{A.A\prime B\prime C\prime }} = \frac{1}{3}d(A;(A\prime B\prime C\prime )).{S_{A\prime B\prime C\prime }}\\
\Rightarrow {V_{MA\prime B\prime C\prime }} = {V_{A.A\prime B\prime C\prime }}.
\end{array}\)
Chọn (D).
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 1 trang 127 SGK Hình học 12 NC
Bài tập 2 trang 127 SGK Hình học 12 NC
Bài tập 4 trang 128 SGK Hình học 12 NC
Bài tập 5 trang 128 SGK Hình học 12 NC
Bài tập 6 trang 128 SGK Hình học 12 NC
Bài tập 7 trang 128 SGK Hình học 12 NC
Bài tập 8 trang 129 SGK Hình học 12 NC
Bài tập 9 trang 129 SGK Hình học 12 NC
Bài tập 10 trang 129 SGK Hình học 12 NC
Bài tập 12 trang 129 SGK Hình học 12 NC
Bài tập 11 trang 129 SGK Hình học 12 NC
Bài tập 13 trang 129 SGK Hình học 12 NC
Bài tập 14 trang 130 SGK Hình học 12 NC
Bài tập 15 trang 130 SGK Hình học 12 NC
Bài tập 16 trang 130 SGK Hình học 12 NC
Bài tập 17 trang 130 SGK Hình học 12 NC
Bài tập 18 trang 130 SGK Hình học 12 NC
Bài tập 19 trang 131 SGK Hình học 12 NC
Bài tập 21 trang 131 SGK Hình học 12 NC
Bài tập 22 trang 131 SGK Hình học 12 NC
Bài tập 23 trang 132 SGK Hình học 12 NC
Bài tập 1 trang 168 SBT Hình học Toán 12
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 4 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


Trong không gian \(Oxyz,\) mặt phẳng \(\left( P \right):2x - 3y + z - 7 = 0\) có một vectơ pháp tuyến là đáp án
bởi Ho Ngoc Ha
 10/06/2021
10/06/2021
A. \(\overrightarrow {{n_1}} = \left( {2;3; - 1} \right).\)
B. \(\overrightarrow {{n_2}} = \left( {1;3;2} \right).\)
C. \(\overrightarrow {{n_3}} = \left( {2; - 3;1} \right).\)
D. \(\overrightarrow {{n_4}} = \left( { - 1;3;2} \right).\)
Theo dõi (0) 1 Trả lời -


Cho biết hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\) và chiều cao bằng \(2a\). Diện tích xung quanh của hình nón đỉnh \(S\)và đáy là hình tròn nội tiếp \(ABCD\) là
bởi Anh Nguyễn
 10/06/2021
10/06/2021
A. \(\frac{{\pi {a^2}\sqrt {17} }}{6}\) B. \(\frac{{\pi {a^2}\sqrt {17} }}{4}\)
C. \(\frac{{\pi {a^2}\sqrt {17} }}{8}\) D. \(\frac{{\pi {a^2}\sqrt {15} }}{4}\)
Theo dõi (0) 1 Trả lời -


Cho đường thẳng \(d\) đi qua điểm \(M\left( {1; - 2;1} \right)\) và vuông góc với mặt phẳng \(x - 2y + 3z - 4 = 0\) có phương trình là
bởi Nguyễn Trà Giang
 10/06/2021
10/06/2021
A. \(\frac{{x - 1}}{1} = \frac{{y + 2}}{2} = \frac{{z - 1}}{{ - 3}}\).
B. \(\frac{{x + 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z - 1}}{3}\).
C. \(\frac{{x + 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z + 5}}{3}\).
D. \(\frac{{x - 1}}{1} = \frac{{y + 2}}{{ - 2}} = \frac{{z + 1}}{3}\).
Theo dõi (0) 1 Trả lời -


Trong không gian với hệ tọa độ, ta cho mặt phẳng \(\left( P \right):\, - x + y + 3z - 2 = 0\). Phương trình mặt phẳng \(\left( \alpha \right)\) đi qua \(A\left( {2;\, - 1;\,1} \right)\) và song song với \(\left( P \right)\) là
bởi Phan Quân
 10/06/2021
10/06/2021
A. \(x - y + 3z - 6 = 0\).
B. \( - x + y - 3z = 0\)
C. \( - x + y + 3z = 0\)
D. \( - x - y + 3z = 0\)
Theo dõi (0) 1 Trả lời -
ADMICRO


Trong không gian với hệ toạ độ , cho hai đường thẳng \({\Delta _1}:\frac{{x + 1}}{1} = \frac{{y - 2}}{2} = \frac{{z + 1}}{3}\) và \({\Delta _2}:\frac{{x + 1}}{1} = \frac{{y - 2}}{2} = \frac{{z + 1}}{{ - 3}}\). Đường thẳng \(d\) đi qua điểm \(M\left( {1;1;3} \right)\) và vuông góc với cả hai đường thẳng \({\Delta _1};{\Delta _2}\) có phương trình là câu?
bởi hi hi
 10/06/2021
10/06/2021
A. \(\left\{ \begin{array}{l}x = 1 + t\\y = 1 + t\\z = 3 + 3t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 - t\\z = 3\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = - 12 + t\\y = 6 + t\\z = 3t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 1 - 2t\\y = 1 + t\\z = 3 - t\end{array} \right.\)
Theo dõi (0) 1 Trả lời -


Ở không gian \(Oxyz\), hình chiếu vuông góc của điểm \(M\left( {3; - 2;1} \right)\) trên mặt phẳng \(\left( {Oxz} \right)\) có tọa độ là
bởi Duy Quang
 10/06/2021
10/06/2021
A. \(\left( {0; - 2;1} \right)\).
B. \(\left( {0;0;1} \right)\).
C. \(\left( {3;0;1} \right)\).
D. \(\left( {3; - 2;0} \right)\).
Theo dõi (0) 1 Trả lời -


Cho tứ diện \(SABC\), có \(SA,\,SB,\,SC\) đôi một vuông góc. Và biết \(SA = a,SB = a;SC = 2a\). Tính khoảng cách từ điểm \(S\) đến mặt phẳng \(\left( {ABC} \right)\)
bởi hành thư
 10/06/2021
10/06/2021
A. \(\frac{{2a}}{3}\).
B. \(\frac{a}{2}\).
C. \(\frac{{a\sqrt 2 }}{2}\).
D. \(\frac{{2a\sqrt 5 }}{5}\).
Theo dõi (0) 1 Trả lời -


Có hình chóp \(S.ABC\). Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SA,\,\,SB,\,\,SC\). Tỉ số thể tích \(\frac{{{V_{S.ABC}}}}{{{V_{S.MNP}}}}\) bằng
bởi Meo Thi
 10/06/2021
10/06/2021
A. \(2\). B. \(8\).
C. \(12\). D. \(3\).
Theo dõi (0) 1 Trả lời -


Ở không gian \(Oxyz\), cho mặt phẳng \(\left( P \right)\) có phương trình : \(2x - 3y + z + 4 = 0\). Véc tơ nào dưới đây là một véc tơ pháp tuyến của mặt phẳng \(\left( P \right)\)
bởi My Le
 10/06/2021
10/06/2021
A. \(\left( { - 2;3;4} \right)\).
B. \(\left( {2; - 3;4} \right)\).
C. \(\left( {2; - 3;0} \right)\).
D. \(\left( {2; - 3;1} \right)\).
Theo dõi (0) 1 Trả lời -


Trong không gian \(Oxyz\), cho đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y - 2}}{3} = \frac{{z + 2}}{{ - 1}}\). Biết điểm nào dưới đây thuộc đường thẳng \(d\)
bởi Cam Ngan
 10/06/2021
10/06/2021
A. \(\left( {5;1; - 4} \right)\).
B. \(\left( { - 1; - 1;1} \right)\).
C. \(\left( {3;5; - 3} \right)\).
D. \(\left( {1;2;2} \right)\).
Theo dõi (0) 1 Trả lời -


Trong không gian \(Oxyz\), ta có hai điểm \(A\left( {1; - 2;1} \right)\)và \(B\left( { - 1;0;3} \right)\). Phương trình mặt phẳng trung trực của đoạn \(AB\) là
bởi Mai Rừng
 09/06/2021
09/06/2021
A. \( - x + y + z - 6 = 0\).
B. \(x - y - z + 4 = 0\).
C. \(x - y - z + 1 = 0\).
D. \(x - y - z - 2 = 0\).
Theo dõi (0) 1 Trả lời -


Cho biết khối chóp \(S.ABCD\) có thể tích bằng \(2{a^3}\), đáy \(ABCD\) là hình thang với đáy lớn là \(AB\) và \(AB = 3CD\). Gọi \(M\) là trung điểm cạnh \(SA\), \(N\) là điểm thuộc cạnh \(CB\) sao cho \(BN = 3NC\). Mặt phẳng \(\left( {DMN} \right)\) cắt cạnh \(SB\) tại \(I\). Tính thể tích khối chóp \(A.MDNI\).
bởi Thùy Trang
 10/06/2021
10/06/2021
A. \(\frac{{3{a^3}}}{8}\). B. \(\frac{{5{a^3}}}{8}\).
C. \(\frac{{10{a^3}}}{{12}}\). D. \(\frac{{3{a^3}}}{4}\).
Theo dõi (0) 1 Trả lời


