Bài tập 1 trang 127 SGK Hình học 12 NC
Cho H là hình chóp tứ giác đều S.ABCD. Xét các mặt phẳng (SAC), (SAB), (SBD), (ABC), (SOI), trong đó I là trung điểm của AB, O là tâm hình vuông ABCD. Trong các mặt phẳng đó, có bao nhiêu mặt phẳng là mặt phẳng đối xứng của H ?
(A) 1
(B) 2
(C) 3
(D) 4
Hướng dẫn giải chi tiết
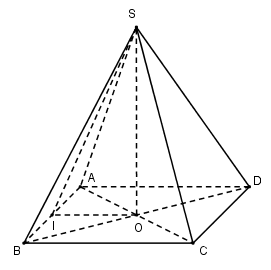
Có 3 mặt phẳng đối xứng của H, đó là: mp(SAC), mp(SBD), mp(SOI).
Chọn (C).
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 9 trang 123 SGK Hình học 12 NC
Bài tập 10 trang 123 SGK Hình học 12 NC
Bài tập 2 trang 127 SGK Hình học 12 NC
Bài tập 3 trang 127 SGK Hình học 12 NC
Bài tập 4 trang 128 SGK Hình học 12 NC
Bài tập 5 trang 128 SGK Hình học 12 NC
Bài tập 6 trang 128 SGK Hình học 12 NC
Bài tập 7 trang 128 SGK Hình học 12 NC
Bài tập 8 trang 129 SGK Hình học 12 NC
Bài tập 9 trang 129 SGK Hình học 12 NC
Bài tập 10 trang 129 SGK Hình học 12 NC
Bài tập 12 trang 129 SGK Hình học 12 NC
Bài tập 11 trang 129 SGK Hình học 12 NC
Bài tập 13 trang 129 SGK Hình học 12 NC
Bài tập 14 trang 130 SGK Hình học 12 NC
Bài tập 15 trang 130 SGK Hình học 12 NC
Bài tập 16 trang 130 SGK Hình học 12 NC
Bài tập 17 trang 130 SGK Hình học 12 NC
Bài tập 18 trang 130 SGK Hình học 12 NC
Bài tập 19 trang 131 SGK Hình học 12 NC
Bài tập 21 trang 131 SGK Hình học 12 NC
Bài tập 22 trang 131 SGK Hình học 12 NC
Bài tập 23 trang 132 SGK Hình học 12 NC
Bài tập 1 trang 168 SBT Hình học Toán 12
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 4 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


Trong mặt phẳng phức \(Oxy\), các số phức \(z\) thỏa \(\left| {z - 5i} \right| \le 3\). Nếu có số phức \(z\) có môđun nhỏ nhất thì phần ảo bằng bao nhiêu?
bởi bich thu
 10/06/2021
10/06/2021
A. \(2\). B. \(4\).
C. \(0\). D. \(3\)
Theo dõi (0) 1 Trả lời -


Biết tích vô hướng của hai vectơ \(\overrightarrow a = \left( { - 2;2;5} \right),\,\overrightarrow b = \left( {0;1;2} \right)\) trong không gian bằng
bởi Huy Tâm
 10/06/2021
10/06/2021
A. \(12\). B. \(14\).
C. \(10\). D. \(13\).
Theo dõi (0) 1 Trả lời -


Biết thể tích khối tam diện vuông \(O.ABC\) vuông tại \(O\) có \(OA = a,{\rm{ }}OB = OC = 2a\) là
bởi Lê Minh Hải
 10/06/2021
10/06/2021
A. \(2{a^3}\).
B. \(\frac{{{a^3}}}{2} \cdot \)
C. \(\frac{{{a^3}}}{6} \cdot \)
D. \(\frac{{2{a^3}}}{3}\)
Theo dõi (0) 1 Trả lời -


Ta cho một mặt cầu có diện tích là \(S\), thể tích khối cầu đó là \(V\). Tính bán kính \(R\) của mặt cầu.
bởi Nguyễn Quang Minh Tú
 10/06/2021
10/06/2021
A. \(R = \frac{{4V}}{S}\). B. \(R = \frac{V}{{3S}}\)
C. \(R = \frac{{3V}}{S}\). D. \(R = \frac{S}{{3V}}\)
Theo dõi (0) 1 Trả lời -
ADMICRO


Các điểm \(I\left( {1;1; - 2} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = - 1 + t\\y = 3 + 2t\\z = 2 + t\end{array} \right.\). Phương trình mặt cầu \(\left( S \right)\)có tâm \(I\) và cắt đường thẳng \(d\) tại hai điểm \(A,B\) sao cho tam giác \(IAB\) vuông là:
bởi na na
 10/06/2021
10/06/2021
A. \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 2} \right)^2} = 9.\)
B. \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 2} \right)^2} = 36.\)
C. \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 2} \right)^2} = 3.\)
D. \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 2} \right)^2} = 9.\)
Theo dõi (0) 1 Trả lời -


Trong không gian với hệ trục toạ độ \(Oxyz\), cho mặt phẳng \((\alpha ):\,\,x\,\, + \,\,2y\,\, + 3z - \,\,2020\,\, = \,\,0;\) đường thẳng \(d:\,\,\frac{{x\,\, - \,\,1}}{1}\,\, = \,\,\frac{{1 - \,\,y}}{2}\,\, = \,\,\frac{{z\,\, + \,\,3}}{3}\). Góc giữa đường thẳng \(d\) và mặt phẳng \((\alpha )\) là đáp án:
bởi hà trang
 10/06/2021
10/06/2021
A. \(60^\circ .\) B. \(45^\circ .\)
C. \(30^\circ .\) D. \(90^\circ .\)
Theo dõi (0) 1 Trả lời -


Biết trong không gian với hệ toạ độ \(Oxyz\) , cho \(A\left( {a;0;0} \right),B\left( {0;b;0} \right);\) \(C\left( {0;0;c} \right),\left( {abc \ne 0} \right)\). Khi đó phương trình mặt phẳng \(\left( {ABC} \right)\) là:
bởi Lan Anh
 10/06/2021
10/06/2021
A.\(\frac{x}{c} + \frac{y}{b} + \frac{z}{a} = 1\)
B. \(\frac{x}{b} + \frac{y}{a} + \frac{z}{c} = 1\)
C. \(\frac{x}{a} + \frac{y}{c} + \frac{z}{b} = 1\)
D. \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\)
Theo dõi (0) 1 Trả lời -


Biết trong không gian \(Oxyz,\) cho ba điểm \(A(1;0;0),\,B(3;2;4),\,C(0;5;4)\). Gọi \(M(a;b;c)\) là điểm thuộc mặt phẳng \((Oyz)\)sao cho biểu thức \(T = M{A^2} + M{B^2} + 2M{C^2}\) đạt giá trị nhỏ nhất. Khi đó \(a + b + c\)bằng
bởi Nguyễn Thủy Tiên
 09/06/2021
09/06/2021
A. 0. B. 6.
C. 5. D. 2.
Theo dõi (0) 1 Trả lời -


Biết trong không gian Oxyz, cho điểm \(A\left( {2;0;0} \right)\) và mặt phẳng \(\left( P \right):3y - 3z + 7 = 0.\) Trên các tia Oy, Oz lần lượt lấy các điểm \(B,C\) phân biệt sao cho mặt phẳng \(\left( {ABC} \right)\) vuông góc với mặt phẳng \(\left( P \right)\) và khoảng cách từ gốc tọa độ \(O\) đến mặt phẳng \(\left( {ABC} \right)\) bằng \(\sqrt 2 .\) Xác định tọa độ điểm B và điểm \(C.\)
bởi An Duy
 10/06/2021
10/06/2021
A. \(B\left( {0;2\sqrt 2 ;0} \right),C\left( {0;0;2\sqrt 2 } \right).\)
B. \(B\left( {0;4;0} \right),C\left( {0;0;4} \right).\)
C. \(B\left( {0;2\sqrt 6 ;0} \right),C\left( {0;0;2\sqrt 6 } \right).\)
D. \(B\left( {0;16;0} \right),C\left( {0;0;16} \right).\)
Theo dõi (0) 1 Trả lời -


Vòm cửa lớn của một trung tâm thương mại có dạng parabol như hình vẽ, trong đó khoảng cách \(AB = 8\,{\rm{m}}\) và chiều cao của vòm cửa là \(CH = 7\,{\rm{m}}.\) Người ta cần ốp kính cho toàn bộ vòm cửa này, khi đó diện tích kính cần dùng ít nhất là bằng:
bởi Nguyễn Sơn Ca
 10/06/2021
10/06/2021
.jpg)
A. \(\frac{{115}}{3}{{\rm{m}}^2}.\) B. \(\frac{{120}}{3}{{\rm{m}}^2}.\)
C. \(\frac{{110}}{3}{{\rm{m}}^2}.\) D. \(\frac{{112}}{3}{{\rm{m}}^2}.\)
Theo dõi (0) 1 Trả lời -


Biết trong không gian \(Oxyz\), cho các điểm \(A(6;0;0),B(0;0;6),C(0;6;6).\) Xét các điểm \(M,N\) di chuyển trên các đoạn \(AB\)và \(OC\) sao cho \(AM = ON.\) Khi độ dài đoạn thẳng \(MN\) nhỏ nhất, phương trình đường thẳng \(MN\) là
bởi Sam sung
 10/06/2021
10/06/2021
A. \(\left\{ \begin{array}{l}x = t\\y = 0\\z = 0.\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = 2 - t\\y = t\\z = 4 - t.\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 3 + t\\y = - t\\z = 3.\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = 0\\y = t\\z = 6.\end{array} \right.\)
Theo dõi (0) 1 Trả lời -


Biết trong không gian \(Oxyz\), cho điểm \(A\left( {2;\,1;\,3} \right)\) và đường thẳng \(d:\frac{{x + 1}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z - 2}}{2} \cdot \) Đường thẳng đi qua \(A\), vuông góc với \(d\) và cắt trục \(Oy\) có phương trình là
bởi Lê Chí Thiện
 10/06/2021
10/06/2021
A. \(\frac{x}{2} = \frac{{y + 3}}{4} = \frac{z}{3} \cdot \)
B. \(\frac{{x - 2}}{2} = \frac{{y - 1}}{1} = \frac{{z - 3}}{3} \cdot \)
C. \(\frac{{x - 2}}{2} = \frac{{y - 1}}{3} = \frac{{z - 3}}{2} \cdot \)
D. \(\frac{x}{2} = \frac{{y + 3}}{3} = \frac{z}{2} \cdot \)
Theo dõi (0) 1 Trả lời



