Bài tập 4 trang 169 SBT Hình học Toán 12
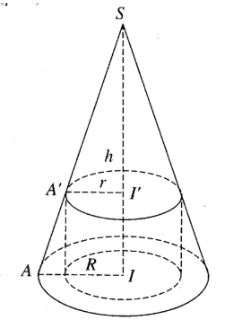
Cho hình nón tròn xoay (H) đỉnh S, đáy là hình tròn bán kính R, chiều cao bằng h.
Gọi (H') là hình trụ tròn xoay có đáy là hình tròn bán kính r (0 < r < R) nội tiếp (H).
a) Tính tỉ số thể tích của (H') và (H);
b) Xác định r để (H') có thể tích lớn nhất.
Hướng dẫn giải chi tiết Bài tập 4 trang 169
a) Giả sử đường cao SI của hình nón (H) cắt hai đáy của hình trụ (H') tại I và I'.
Khi đó \(\frac{r}{R} = \frac{{SI'}}{h}\) \( \Rightarrow \frac{{R - r}}{R} = \frac{{h - SI'}}{h} = \frac{{I'I}}{h}\)
Từ đó suy ra \(I'I = \frac{{h\left( {R - r} \right)}}{R}\)
\({V_{\left( H \right)}} = \frac{1}{3}\pi {R^2}h\)
\({V_{\left( {H'} \right)}} = \frac{1}{3}\pi {r^2}.\frac{{h\left( {R - r} \right)}}{R}\)
Do đó \(\frac{{{V_{\left( {H'} \right)}}}}{{{V_{\left( H \right)}}}} = \frac{{{r^2}\left( {R - r} \right)}}{{{R^3}}}\)
b) V(H') lớn nhất khi f(r) = r2(R - r) (với 0 < r < R) là lớn nhất.
Khảo sát hàm số f(r), với 0 < r < R.
Ta có f'(r) = 2Rr - 3r2 = 0, khi r = 0 (loại), hoặc r = 2R/3.
Lập bảng biến thiên ta thấy f(r) đạt cực đại tại r = 2R/3.
Khi đó \({V_{\left( {H'} \right)}} = \frac{4}{{81}}\pi {R^2}h\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


Nếu một khối cầu có bán kính bằng R thì có thể tích bằng kết quả nào?
bởi hi hi
 08/06/2021
08/06/2021
A. \(4\pi {R^3}.\)
B. \(\dfrac{4}{3}\pi {R^2}.\)
C. \(4\pi {R^2}.\)
D. \(\dfrac{4}{3}\pi {R^3}.\)
Theo dõi (0) 1 Trả lời -


Cắt khối nón bởi một mặt phẳng qua trục, thiết diện là một tam giác đều có diện tích bằng \(25\sqrt 3 {a^2}\). Thể tích của khối nón đó có kết quả:
bởi Mai Trang
 08/06/2021
08/06/2021
A. \(\dfrac{{125\sqrt 3 \pi {a^3}}}{3}\)
B. \(\dfrac{{125\sqrt 3 \pi {a^3}}}{6}\)
C. \(\dfrac{{125\sqrt 3 \pi {a^3}}}{9}\)
D. \(\dfrac{{125\sqrt 3 \pi {a^3}}}{{12}}\)
Theo dõi (0) 1 Trả lời -


A. \(V = \dfrac{{32\pi }}{3}\)
B. \(V = \dfrac{{33\pi }}{3}\)
C. \(V = 16\pi \)
D. \(V = 32\pi \)
Theo dõi (0) 1 Trả lời -


Cho lăng trụ đứng say đây \(ABC.A'B'C'\) có đáy là tam giác vuông tại \(A\). Biết \(AA' = a\sqrt 3 ,\,\,AB = a\sqrt 2 \) và \(AC = 2a\). Thể ích của khối lăng trụ \(ABC.A'B'C'\) là
bởi Ha Ku
 08/06/2021
08/06/2021
A. \(V = {a^3}\sqrt 6 \) B. \(V = \dfrac{{{a^3}\sqrt 6 }}{3}\)
C. \(V = 2{a^3}\sqrt 6 \) D. \(V = \dfrac{{2{a^3}\sqrt 6 }}{3}\)
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho khối chóp tam giác \(S.ABC\). Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SA,\,\,SB,\,\,SC\). Tỉ số giữa thể tích của khối chóp \(S.MNP\) và khối chóp \(S.ABC\) là đáp án?
bởi Bánh Mì
 08/06/2021
08/06/2021
A. \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{1}{6}\)
B. \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{1}{8}\)
C. \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = 8\)
D. \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = 6\)
Theo dõi (0) 1 Trả lời -


A. \(V = 24\) B. \(V = 8\)
C. \(V = 9\) D. \(V = 20\)
Theo dõi (0) 1 Trả lời -


Cho hình nón có bán kính đường tròn đáy là \(r = 3a\) và đường sinh \(l = 2r.\) Diện tích xung quanh của hình nón bằng:
bởi Phạm Khánh Ngọc
 08/06/2021
08/06/2021
A. \(6\pi {a^2}.\) B.\(9\pi {a^2}.\)
C.\(36\pi {a^2}.\) D. \(18\pi {a^2}.\)
Theo dõi (0) 1 Trả lời -


Thể tích của khối chóp có diện tích đáy \(B\) và chiều cao \(h\) có kết quả:
bởi Phạm Khánh Ngọc
 08/06/2021
08/06/2021
A. \(V = Bh.\) B.\(V = \dfrac{1}{3}Bh.\)
C. \(V = 3Bh.\) D. \(V = \dfrac{2}{3}Bh.\)
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 4a,\,AC = 3a.\) Quay \(\Delta ABC\) xung quanh cạnh \(AB,\) đường gấp khúc \(ACB\) tạo nên một hình nón tròn xoay, Diện tích xung quanh của hình nón đó có đáp án:
bởi Nguyen Ngoc
 08/06/2021
08/06/2021
A. \({S_{xq}} = 24\pi {a^2}.\) B. \({S_{xq}} = 12\pi {a^2}.\)
C. \({S_{xq}} = 30\pi {a^2}.\) D. \({S_{xq}} = 15\pi {a^2}.\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABCD} \right),\,\,ABCD\) là hình chữ nhật, \(AB = 2BC = 2a,\,SC = 3a.\) Thể tích khối chóp \(S.ABCD\) có kết quả:
bởi thu trang
 08/06/2021
08/06/2021
A.\({a^3}.\)
B. \(\dfrac{{4{a^3}}}{3}.\)
C. \(\dfrac{{{a^3}}}{3}.\)
D. \(\dfrac{{2{a^3}}}{3}.\)
Theo dõi (0) 1 Trả lời -


Cho khối trụ có chiều cao là \(h = 4a\) và bán kính đường tròn đáy \(r = 2a.\) Thể tích của khối trụ đã cho bằng
bởi Ngoc Son
 08/06/2021
08/06/2021
A. \(8\pi {a^3}.\) B. \(16\pi {a^3}.\)
C. \(6\pi {a^3}.\) D. \(\dfrac{{16\pi {a^3}}}{3}.\)
Theo dõi (0) 1 Trả lời -


Cho hình chữ nhật \(ABCD\) có \(AB = 2a\sqrt 3 ,\,\widehat {ADB} = 60^\circ .\) Gọi \(M,\,N\) lần lượt là trung điểm của \(AD,\,BC.\) Khối trụ tròn xoay tạo thành khi quay hình chữ nhật \(ABCD\) (kể cả điểm trong) xung quanh cạnh \(MN\) có thể tích bằng bao nhiêu ?
bởi minh thuận
 08/06/2021
08/06/2021
A. \(V = 8\pi {a^3}\sqrt 3 .\)
B. \(V = \dfrac{{2\pi {a^3}\sqrt 3 }}{3}.\)
C. \(V = 2\pi {a^3}\sqrt 3 .\)
D.\(V = \dfrac{{8\pi {a^3}\sqrt 3 }}{3}.\)
Theo dõi (0) 1 Trả lời