Bài tập 1 trang 168 SBT Hình học Toán 12
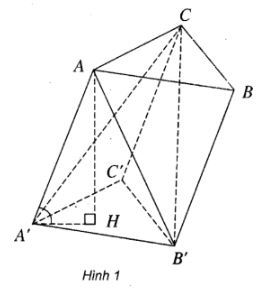
Cho lăng trụ ABC.A'B'C'
a) Tính tỉ số \(\frac{{{V_{ACA'B'}}}}{{{V_{ABC.A'B'C'}}}}\)
b) Tính VACA'B' biết rằng tam giác ABC là tam giác đều cạnh bằng a, AA' = b và AA' tạo với (ABC) một góc bằng 60o
Hướng dẫn giải chi tiết Bài tập 1 trang 168
a) Ta có: VACA'B' = VB'.ACA' = VB'.CA'C' = VC.A'B'C' = VABC.A'B'C'/3
Từ đó suy ra tỉ số phải tìm bằng 1/3.
b) Gọi H là chân đường cao đi qua A của lăng trụ.
\( \Rightarrow \left( {AA',\left( {A'B'C'} \right)} \right) = \left( {AA',A'H} \right)\) \( = \widehat {AA'H} = {60^0}\)
Tam giác vuông AA’H có \(AH = AA'\sin {60^0} = \frac{{b\sqrt 3 }}{2}\)
Lại có \({S_{A'B'C'}} = \frac{1}{2}A'B'.A'C'.\sin \widehat {B'A'C'}\) \( = \frac{1}{2}.a.a.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}\)
Do đó: \({V_{ABC.A'B'C'}} = {S_{A'B'C'}}.AH\) \( = \frac{{{a^2}\sqrt 3 }}{4}.\frac{{b\sqrt 3 }}{2} = \frac{{3{a^2}b}}{8}\)
Suy ra \({V_{ACA'B'}} = \frac{1}{3}{V_{ABC.A'B'C'}} \) \(= \frac{1}{3}.\frac{{3{a^2}b}}{8} = \frac{{{a^2}b}}{8}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 23 trang 132 SGK Hình học 12 NC
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 4 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


Trong không gian Oxyz, cho mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 4x + 6z - 2 = 0\) có bán kính bằng
bởi Bùi Anh Tuấn
 09/06/2021
09/06/2021
A. \(\sqrt {11} \)
B. \(3\sqrt 6 \)
C. \(2\sqrt 3 \)
D. \(\sqrt {15} \)
Theo dõi (0) 1 Trả lời -


A. \(3 + 2i\)
B. \(2 + 3i\)
C. \(2 - 3i\)
D. \(3 - 2i\)
Theo dõi (0) 1 Trả lời -


Trong không gian Oxyz, có hai điểm \(A\left( {1;1; - 2} \right)\) và \(B\left( {3;0;1} \right)\). Vecto \(\overrightarrow {AB} \) có tọa độ là
bởi Bùi Anh Tuấn
 09/06/2021
09/06/2021
A. \(\left( {4;1; - 1} \right)\)
B. \(\left( {2;\dfrac{1}{2}; - \dfrac{1}{2}} \right)\)
C. \(\left( {2; - 1;3} \right)\)
D. \(\left( { - 2;1; - 3} \right)\)
Theo dõi (0) 1 Trả lời -


Có khối tứ diện ABCD có thể tích bằng V. Gọi M là trung điểm cạnh AB, N thuộc cạnh AC sao cho AN = 2 NC, P thuộc cạnh AD sao cho PD = 3 AP. Thể tích của khối đa diện MNP.BCD tính theo V là
bởi hai trieu
 08/06/2021
08/06/2021
A. \(\dfrac{{21}}{{24}}V\)
B. \(\dfrac{5}{6}V\)
C. \(\dfrac{7}{8}V\)
D. \(\dfrac{{11}}{{12}}V\)
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho hình chóp đều S.ABCD có cạnh đáy bằng 4cm và chiều cao là bằng 2cm . Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng
bởi hi hi
 09/06/2021
09/06/2021
A. \(4,5cm.\)
B. \(3cm.\)
C.\(6cm.\)
D. \(4cm.\)
Theo dõi (0) 1 Trả lời -


Tìm tất cả giá trị thực của tham số m sao cho hàm số sau \(y = 4{{\rm{x}}^3} + m{{\rm{x}}^2} - 12{\rm{x}} + 5\) đạt cực tiểu tại điểm x = -2.
bởi Lan Ha
 09/06/2021
09/06/2021
A. Không tồn tại giá trị của m.
B. \(m = \dfrac{3}{4}\).
C.\(m = {\rm{ }}0.\)
D. \(m = {\rm{ }}9.\)
Theo dõi (0) 1 Trả lời -


Biết tthể tích của khối cầu đường kính 3R bằng kết quả
bởi Hoang Vu
 09/06/2021
09/06/2021
A.\(\dfrac{{9\pi {R^3}}}{8}\)
B. \(\dfrac{{27\pi {R^3}}}{8}\).
C. \(\dfrac{{9\pi {R^3}}}{2}\).
D. \(36\pi {R^3}\)
Theo dõi (0) 1 Trả lời -


Trong không gian cho hai điểm phân biệt A, B cố định. Cho biết tập hợp các điểm M thỏa mãn đẳng thức \(\overrightarrow {MA} .\overrightarrow {MB} = 0\) là
bởi hi hi
 09/06/2021
09/06/2021
A. Mặt cầu bán kính AB.
B. Hình tròn bán kính AB.
C. Mặt cầu đường kính AB.
D. Hình tròn đường kính AB.
Theo dõi (0) 1 Trả lời -


Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Gọi M là trung điểm của SA. Thể tích của khối chóp M.ABC bằng đáp án?
bởi Lê Gia Bảo
 09/06/2021
09/06/2021
A. \(\dfrac{{\sqrt {13} {a^3}}}{{12}}\) .
B. \(\dfrac{{\sqrt {11} {a^3}}}{{48}}\)
C. \(\dfrac{{\sqrt {11} {a^3}}}{8}\).
D. \(\dfrac{{\sqrt {11} {a^3}}}{{24}}\)
Theo dõi (0) 1 Trả lời -


A. \(5.\)
B.\(2.\)
C.\(4.\)
D. \(3.\)
Theo dõi (0) 1 Trả lời -


Với hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh SA vuông góc với mặt phẳng (ABCD), góc giữa cạnh SD và mặt phẳng (ABCD) bằng \(60^\circ \). Thể tích của khối chóp đã cho bằng:
bởi bala bala
 09/06/2021
09/06/2021
A. \(\sqrt 3 {a^3}\)
B. \(\dfrac{{\sqrt 3 {a^3}}}{6}\)
C. \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
D. \(\dfrac{{\sqrt 3 {a^3}}}{9}\)
Theo dõi (0) 1 Trả lời -


Ta có một hình trụ có diện tích xung quanh bằng \(S,\) diện tích đáy bằng diện tích một mặt cầu bán kính \(a,\) khi đó thể tích của hình trụ bằng :
bởi Trần Bảo Việt
 08/06/2021
08/06/2021
A. \(Sa.\)
B. \(\dfrac{1}{3}Sa.\).
C. \(\dfrac{1}{4}Sa.\)
D. \(\dfrac{1}{2}Sa.\)
Theo dõi (0) 1 Trả lời