Bài tập 6 trang 123 SGK Hình học 12 NC
Cho hình lục giác đều ABCDEF cạnh a.
a) Tính thể tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường thẳng AD.
b) Tính thế tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường thẳng đi qua trung điểm của các cạnh AB và DE.
Hướng dẫn giải chi tiết
a)
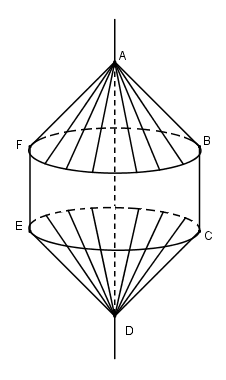
Khi quay lục giác dều ABCDEF quanh đường thẳng AD, ta được khối tròn xoay hợp bởi ba khối: Khối nón N1 sinh bởi tam giác ABF, khối trụ T sinh bởi hình chữ nhật BCEF và khối nón N2 sinh bởi tam giác DCE. Hai khối nón và trụ đều có bán kính đáy là \(R = \frac{{BF}}{2} = \frac{{a\sqrt 3 }}{2}\) Khối trụ có chiều cao a và các khối nón có chiều cao \(\frac{a}{2}\)
Vậy khối tròn xoay sinh bởi lục giác đã cho có thể tích là:
\(V = \pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2}a + 2.\frac{1}{3}\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2}.\frac{a}{2} = \pi {a^3}.\)
b)
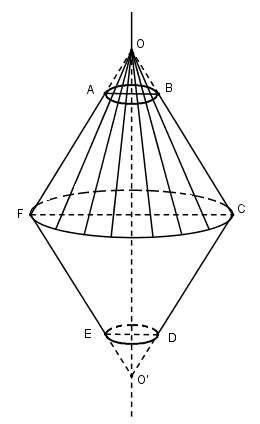
Gọi Δ là đường thẳng nối trung điểm của AB và ED. Khi đó BC và AF cắt nhau tại điểm O trên Δ, CD và FE cắt nhau tại O’ trên Δ. Gọi V, V1, V2 là thể tích các khối tròn xoay lần lượt sinh ra bởi lục giác đều ABCDEF, tam giác OCF và tam giác OAB khi quay quanh Δ, ta có:
\(\begin{array}{l}
{V_1} = \frac{1}{3}\pi {a^2}a\sqrt 3 = \frac{{\pi {a^3}\sqrt 3 }}{3}\\
{V_2} = \frac{1}{3}\pi {\left( {\frac{a}{2}} \right)^2}\frac{{a\sqrt 3 }}{2} = \frac{{\pi {a^3}\sqrt 3 }}{{24}}.
\end{array}\)
Do đó \(V = 2\left( {{V_1} - {V_2}} \right) = \frac{{7\sqrt 3 \pi {a^3}}}{{12}}.\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 4 trang 122 SGK Hình học 12 NC
Bài tập 5 trang 122 SGK Hình học 12 NC
Bài tập 7 trang 123 SGK Hình học 12 NC
Bài tập 8 trang 123 SGK Hình học 12 NC
Bài tập 9 trang 123 SGK Hình học 12 NC
Bài tập 10 trang 123 SGK Hình học 12 NC
Bài tập 1 trang 127 SGK Hình học 12 NC
Bài tập 2 trang 127 SGK Hình học 12 NC
Bài tập 3 trang 127 SGK Hình học 12 NC
Bài tập 4 trang 128 SGK Hình học 12 NC
Bài tập 5 trang 128 SGK Hình học 12 NC
Bài tập 6 trang 128 SGK Hình học 12 NC
Bài tập 7 trang 128 SGK Hình học 12 NC
Bài tập 8 trang 129 SGK Hình học 12 NC
Bài tập 9 trang 129 SGK Hình học 12 NC
Bài tập 10 trang 129 SGK Hình học 12 NC
Bài tập 12 trang 129 SGK Hình học 12 NC
Bài tập 11 trang 129 SGK Hình học 12 NC
Bài tập 13 trang 129 SGK Hình học 12 NC
Bài tập 14 trang 130 SGK Hình học 12 NC
Bài tập 15 trang 130 SGK Hình học 12 NC
Bài tập 16 trang 130 SGK Hình học 12 NC
Bài tập 17 trang 130 SGK Hình học 12 NC
Bài tập 18 trang 130 SGK Hình học 12 NC
Bài tập 19 trang 131 SGK Hình học 12 NC
Bài tập 21 trang 131 SGK Hình học 12 NC
Bài tập 22 trang 131 SGK Hình học 12 NC
Bài tập 23 trang 132 SGK Hình học 12 NC
Bài tập 1 trang 168 SBT Hình học Toán 12
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 4 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


Cho hình lập phương có đường chéo bằng \(2\sqrt 3 \). Thể tích mặt cầu ngoại tiếp hình lập phương đó là bằng
bởi thu trang
 10/06/2021
10/06/2021
A. \(12\sqrt 3 \pi \)
B. \(3\sqrt 3 \pi \)
C. \(\sqrt 3 \pi \)
D. \(4\sqrt 3 \pi \)
Theo dõi (0) 1 Trả lời -


Cho hình nón bán kính đáy bằng 4 . Biết rằng khi cắt hình nón đã cho bởi mặt phẳng đi qua trục ta được thiết diện là một tam giác đều. Diện tích xung quanh của hình nón đã cho là bằng
bởi Van Tho
 11/06/2021
11/06/2021
A. \(16\pi \) B. \(8\pi \) C. \(12\pi \) D. \(32\pi \)
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh 2\(a\), \(SA \bot \left( {ABC} \right)\),\(SA = a\). Thể tích khối chóp \(S.ABC\) bằng câu?
bởi hành thư
 11/06/2021
11/06/2021
A. \(\dfrac{{\sqrt 3 {a^3}}}{3}\) B. \(\sqrt 3 {a^3}\)
C. \(\dfrac{{\sqrt 3 {a^3}}}{{12}}\) D. \(\dfrac{{\sqrt 3 {a^3}}}{4}\)
Theo dõi (0) 1 Trả lời -


Trong không gian \({\rm{Ox}}yz\), tìm hình chiếu \(H\) của điểm \(A(1; - 2;3)\) trên mặt phẳng \({\rm{(Ox}}y)\)
bởi Lê Minh Trí
 11/06/2021
11/06/2021
A. \(H(1; - 2;0)\) B. \(H(1;2;0)\)
C. \(H(0; - 2;3)\) D. \(H(1;0;3)\)
Theo dõi (0) 1 Trả lời -
ADMICRO


Trong không gian\({\rm{Ox}}yz\), gọi \(A,B,C\) lần lượt là hình chiếu vuông góc của điểm \(M( - 1;1;2)\)trên các trục \({\rm{Ox}},Oy,Oz\). Viết phương trình mặt phẳng \((ABC)\) ta được
bởi Hữu Nghĩa
 11/06/2021
11/06/2021
A. \(2x - 2y - z = 0\)
B. \(2x - 2y - z + 2 = 0\)
C. \( - 2x + 2y + z + 2 = 0\)
D. \(2x + 2y - z + 2 = 0\)
Theo dõi (0) 1 Trả lời -


Trong không gian\({\rm{Ox}}yz\). Biết mặt cầu \((S)\) đi qua gốc tọa độ \(O\) và các điểm \(A( - 4;0;0)\), \(B(0;2;0)\), \(C\left( {0;0;4} \right)\). Phương trình \(\left( S \right)\) là:
bởi Lê Viết Khánh
 11/06/2021
11/06/2021
A. \({x^2} + {y^2} + {z^2} + 4x + 2y - 4z = 0\)
B. \({x^2} + {y^2} + {z^2} + 4x - 2y + 4z = 0\)
C. \({x^2} + {y^2} + {z^2} + 4x - 2y - 4z = 0\)
D. \({x^2} + {y^2} + {z^2} + 2x - y - 2z = 0\)
Theo dõi (0) 1 Trả lời -


Cho lăng trụ tam giác đều có tất cả các cạnh đều bằng \(\sqrt 3 \). Thể tích của khối lăng trụ đã cho bằng bao nhiêu?
bởi Khanh Đơn
 11/06/2021
11/06/2021
A. \(\dfrac{9}{2}\) B. \(\dfrac{9}{4}\)
C. \(\dfrac{3}{4}\) D. \(\dfrac{{3\sqrt 3 }}{4}\)
Theo dõi (0) 1 Trả lời -


Trong không gian \({\rm{Ox}}yz\), cho tam giác\(ABC\) có trọng tâm \(G\), biết \(A\left( {1;2;0} \right)\), \(B\left( { - 4;5;3} \right)\), \(G\left( {0; - 1; - 1} \right)\). Tìm tọa độ điểm \(C\)
bởi bach hao
 11/06/2021
11/06/2021
A. \(12\pi \) B. \(C(3; - 10; - 6)\)
C. \(2\pi \sqrt 3 \) D. \(4\pi \sqrt 3 \)
Theo dõi (0) 1 Trả lời -


Trong không gian \({\rm{Ox}}yz\), cho tam giác\(ABC\) có trọng tâm \(G\), biết \(A\left( {1;2;0} \right)\), \(B\left( { - 4;5;3} \right)\), \(G\left( {0; - 1; - 1} \right)\). Tìm tọa độ điểm \(C\)
bởi bach hao
 11/06/2021
11/06/2021
A. \(12\pi \) B. \(C(3; - 10; - 6)\)
C. \(2\pi \sqrt 3 \) D. \(4\pi \sqrt 3 \)
Theo dõi (0) 1 Trả lời -


Trong không gian \({\rm{Ox}}yz\), cho hai điểm \(M( - 1;5;3)\),\(N(1;3;5)\). Hãy viết phương trình mặt phẳng trung trực \((P)\) của đoạn \(MN\).
bởi sap sua
 11/06/2021
11/06/2021
A. \(x - y + z = 0\)
B. \( - x - y + z = 0\)
C. \(x + y + z + 1 = 0\)
D. \(x - y + z - 1 = 0\)
Theo dõi (0) 1 Trả lời -


Trong không gian \(Oxyz\), viết phương trình mặt phẳng \((P)\) đi qua điểm \(A(2;1; - 3)\), song song với trục \(Oz\) và vuông góc với mặt phẳng \((Q):x + y - 3z = 0\).
bởi thùy trang
 11/06/2021
11/06/2021
A. \(x + y - 3 = 0\)
B. \(x - y = 0\)
C. \(x - y - 1 = 0\)
D. \(x - y + 1 = 0\)
Theo dõi (0) 1 Trả lời -


Trong không gian \(Oxyz\), viết phương trình mặt phẳng \((P)\) đi qua điểm \(A(2;1; - 3)\), song song với trục \(Oz\) và vuông góc với mặt phẳng \((Q):x + y - 3z = 0\).
bởi Minh Tú
 11/06/2021
11/06/2021
A. \(x + y - 3 = 0\) B. \(x - y = 0\)
C. \(x - y - 1 = 0\) D. \(x - y + 1 = 0\)
Theo dõi (0) 1 Trả lời



