Bài tập 1 trang 122 SGK Hình học 12 NC
Cho hình lăng trụ ABC.A’B’C’ với cạnh bên không vuông góc với mặt đáy. Gọi (α) là mặt phẳng vuông góc với các cạnh bên của hình lăng trụ và cắt chúng tại P, Q, R. Phép tịnh tiến theo vectơ \(\overrightarrow {AA'}\) biến tam giác PQR thành tam giác P’Q’R’.
a) Chứng minh rằng thể tích V của hình lăng trụ đã cho bằng thể tích của hình lăng trụ PQR.P’Q’R’.
b) Chứng minh rằng V = SPQR.AA′, trong đó SPQR là diện tích tam giác PQR.
Hướng dẫn giải chi tiết
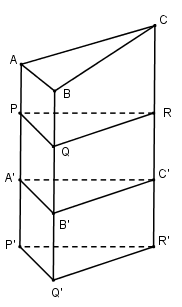
a) Mp(PQR) chia khối lăng trụ ABC.A’B’C’ thành 2 khối đa diện H1 và H2 với H1 chứa ΔABC, H2 chứa ΔA′B′C′.
Mp(A’B’C’) chia khối lăng trụ PQR.P’Q’R’ thành hai khối đa diện H2 và H3 với H3 chứa ΔP′Q′R′.
Gọi V1, V2, V3 lần lượt là thể tích của các khối đa diện H1,H2,H3 ta có:
VABC.A′B′C′ = V1+V2, VPQR.P′Q′R′ = V2+V3.
Phép tịnh tiến \(\overrightarrow {AA'} :\)
\(\begin{array}{l}
{T_{\overrightarrow {AA'} }}:{\rm{\Delta }}ABC \to {\rm{\Delta }}A'B'C'\\
{T_{\overrightarrow {AA'} }}:{\rm{\Delta }}PQR \to {\rm{\Delta }}P'Q'R'
\end{array}\)
Suy ra \({T_{\overrightarrow {AA'} }}:{H_1} \to {H_3}\)
Do đó \({V_1} = {V_3}\)
Vậy \({V_{ABC.A'B'C'}} = {V_{PQR.P'Q'R'}}.\)
b) Vì lăng trụ PQR.P’Q’R’ là lăng trụ đứng nên có chiều cao PP’ = AA’ nên
\({V_{ABC.A'B'C'}} = {V_{PQR.P'Q'R'}} = {S_{PQR}}.AA'.\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 15 trang 101 SGK Hình học 12
Bài tập 16 trang 102 SGK Hình học 12
Bài tập 2 trang 122 SGK Hình học 12 NC
Bài tập 3 trang 122 SGK Hình học 12 NC
Bài tập 4 trang 122 SGK Hình học 12 NC
Bài tập 5 trang 122 SGK Hình học 12 NC
Bài tập 6 trang 123 SGK Hình học 12 NC
Bài tập 7 trang 123 SGK Hình học 12 NC
Bài tập 8 trang 123 SGK Hình học 12 NC
Bài tập 9 trang 123 SGK Hình học 12 NC
Bài tập 10 trang 123 SGK Hình học 12 NC
Bài tập 1 trang 127 SGK Hình học 12 NC
Bài tập 2 trang 127 SGK Hình học 12 NC
Bài tập 3 trang 127 SGK Hình học 12 NC
Bài tập 4 trang 128 SGK Hình học 12 NC
Bài tập 5 trang 128 SGK Hình học 12 NC
Bài tập 6 trang 128 SGK Hình học 12 NC
Bài tập 7 trang 128 SGK Hình học 12 NC
Bài tập 8 trang 129 SGK Hình học 12 NC
Bài tập 9 trang 129 SGK Hình học 12 NC
Bài tập 10 trang 129 SGK Hình học 12 NC
Bài tập 12 trang 129 SGK Hình học 12 NC
Bài tập 11 trang 129 SGK Hình học 12 NC
Bài tập 13 trang 129 SGK Hình học 12 NC
Bài tập 14 trang 130 SGK Hình học 12 NC
Bài tập 15 trang 130 SGK Hình học 12 NC
Bài tập 16 trang 130 SGK Hình học 12 NC
Bài tập 17 trang 130 SGK Hình học 12 NC
Bài tập 18 trang 130 SGK Hình học 12 NC
Bài tập 19 trang 131 SGK Hình học 12 NC
Bài tập 21 trang 131 SGK Hình học 12 NC
Bài tập 22 trang 131 SGK Hình học 12 NC
Bài tập 23 trang 132 SGK Hình học 12 NC
Bài tập 1 trang 168 SBT Hình học Toán 12
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 4 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


Gọi \(A,{\mkern 1mu} {\mkern 1mu} B\) là hai điểm cực trị của đồ thị hàm số \(y = {x^3} - 3x - 2\). Phương trình đường thẳng đi qua hai điểm \(A,{\mkern 1mu} {\mkern 1mu} B\) là bằng
bởi Hoàng My
 11/06/2021
11/06/2021
A. \(x + y + 1 = 0.\) B. \(4x + y = 0.\)
C. \(2x + y + 2 = 0.\) D. \(x + y + 2 = 0.\)
Theo dõi (0) 1 Trả lời -


Cho khối chóp tam giác có thể tích bằng 6. Gọi \(M,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} P\) lần lượt là trung điểm các cạnh \(BC,{\mkern 1mu} {\mkern 1mu} CA,{\mkern 1mu} {\mkern 1mu} AB\). Thể tích của khối chóp S.MNP là bằng?
bởi Khanh Đơn
 11/06/2021
11/06/2021
A. \(V = 4.\) B. \(V = \dfrac{3}{2}.\)
C. \(V = \dfrac{9}{2}.\) D. \(V = 3.\)
Theo dõi (0) 1 Trả lời -


Có hình chóp đều S.ABC có độ dài cạnh đáy 2a, mặt bên tạo với mặt đáy một góc là \({60^0}\). Tính thế tích của khối chóp S.ABC?
bởi Huong Hoa Hồng
 11/06/2021
11/06/2021
A. \(\dfrac{{{a^3}\sqrt 3 }}{3}\) B. \(\dfrac{{{a^3}\sqrt 3 }}{{24}}\)
C. \(\dfrac{{2{a^3}\sqrt 3 }}{3}\) D. \({a^3}\sqrt 3 \)
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABC có \(A',{\mkern 1mu} {\mkern 1mu} B'\) lần lượt là trung điểm của \(SA,{\mkern 1mu} {\mkern 1mu} SB\). Biết thể tích khối chóp S.ABC bằng 24. Có thể tích \(V\) của khối chóp S.A'B'C.
bởi hồng trang
 11/06/2021
11/06/2021
.jpg)
A. \(V = 8\). B. \(V = 12\).
C. \(V = 6\). D. \(V = 3\).
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc với mặt phẳng đáy, \(AB = 2a,{\mkern 1mu} {\mkern 1mu} \widehat {BAC} = {60^0}\) và \(SA = a\sqrt 2 .\) Biết góc giữa đường thẳng SB và mặt phẳng \(\left( {SAC} \right)\) bằng bao nhiêu?
bởi Lê Thánh Tông
 11/06/2021
11/06/2021
A. \({30^0}.\) B. \({45^0}.\) C. \({60^0}.\) D. \({90^0}.\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có đáy là hình thoi cạnh \(a\), \(\angle BAD = {60^0}\), cạnh bên \(SA = a\) và SA vuông góc với mặt phẳng đáy. Khoảng cách từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\) là bằng
bởi Mai Thuy
 11/06/2021
11/06/2021
A. \(\dfrac{{a\sqrt {21} }}{7}\) B. \(\dfrac{{a\sqrt {15} }}{7}\)
C. \(\dfrac{{a\sqrt {21} }}{3}\) D. \(\dfrac{{a\sqrt {15} }}{3}\)
Theo dõi (0) 1 Trả lời -


A. 12 mặt B. 6 mặt C. 10 mặt D. 8 mặt
Theo dõi (0) 1 Trả lời -


Với khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), \(SA = a\), \(AB = a\), \(AC = 2a\), \(BC = a\sqrt 3 .\) Tính thể tích khối chóp S.ABC.
bởi May May
 11/06/2021
11/06/2021
A. \({a^3}\sqrt 3 .\)
B. \(\dfrac{{{a^3}\sqrt 3 }}{6}.\)
C. \(\dfrac{{{a^3}\sqrt 3 }}{2}.\)
D. \(\dfrac{{{a^3}\sqrt 3 }}{3}.\)
Theo dõi (0) 1 Trả lời -


Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích các mặt ABCD, ABB'A', ADD'A' lần lượt bằng \(36c{m^2}\), \(225c{m^2}\), \(100c{m^2}\).Cho biết thể tích khối A.A'B'D'.
bởi trang lan
 11/06/2021
11/06/2021
A. \(900c{m^3}.\) B. \(150c{m^3}.\)
C. \(250c{m^3}.\) D. \(300c{m^3}.\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết \(SB = a\) và SC hợp với (SAB) một góc 300 và (SAC) hợp với (ABC) một góc 600. Thể tích khối chóp là bằng
bởi An Duy
 11/06/2021
11/06/2021
A. \(\dfrac{{{a^3}\sqrt 3 }}{{27}}\)
B. \(\dfrac{{{a^3}\sqrt 3 }}{9}\)
C. \(\dfrac{{{a^3}}}{{27}}\)
D. \(\dfrac{{{a^3}}}{9}\)
Theo dõi (0) 1 Trả lời -


Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là một hình thoi cạnh a, \(\widehat {ABC} = {120^0}\); \(AA' = 4a\) . Hãy tính khoảng cách giữa hai đường thẳng A’C và BB’?
bởi Anh Nguyễn
 11/06/2021
11/06/2021
A. \(\dfrac{{a\sqrt 3 }}{2}\) B. \(a\sqrt 3 \)
C. \(\dfrac{a}{2}\) D. \(\dfrac{a}{{\sqrt 3 }}\)
Theo dõi (0) 1 Trả lời -


A. 26 B. 24 C. 30 D. 22
Theo dõi (0) 1 Trả lời


