Giải bài 3 tr 99 sách GK Toán Hình lớp 12
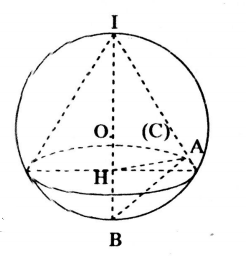
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó.
a) Tính thể tích của hình nón theo r và h.
b) Xác định h để thể tích của hình nón là lớn nhất.
Hướng dẫn giải chi tiết bài 3
Câu a:
Gọi H là tâm đường tròn (C), IB là đường kính mặt cầu.
Suy ra: \(H,O \in IB\)
Lấy A là 1 điểm trên (C).
Ta có tam giác IHA đồng dạng với tam giác IAB.
Suy ra: \(\frac{IH}{IA}=\frac{IA}{IB}\Rightarrow IA^2=IH.IB=h.2r=2rh.\)
Mặc khác:
\(\begin{array}{l} I{A^2} = I{H^2} + H{A^2}\\ \Rightarrow H{A^2} = I{A^2} - I{H^2} = 2rh - {h^2} = h(2r - h). \end{array}\)
Vậy đường tròn (C) có bán kính là: \(R = \sqrt {h(2r - h)} .\)
Thể tích của khối nón là: \(V = \frac{1}{3}\pi .{R^2}.h = \frac{1}{3}.\pi .h(2R - h).h = \frac{1}{3}.\pi (2r - h){h^2}.\)
Câu b:
Xét hàm số \(V(h) = \left( {2r - h} \right).{h^2}\) với \(0<h<2r.\)
Ta có:
\(\begin{array}{l} V'(h) = - 3{h^2} + 4rh = h( - 3h + 4r)\\ V'(h) = 0 \Leftrightarrow \left[ \begin{array}{l} h = 0 \notin \left( {0;2r} \right)\\ h = \frac{{4r}}{3} \in \left( {0;2r} \right) \end{array} \right. \end{array}\)
Bảng biến thiên:
Vậy thể tích khối nón lớn nhất là \(V=\frac{{32}}{{81}}{r^3}\) khi \(h = \frac{4}{3}r.\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 1 trang 99 SGK Hình học 12
Bài tập 2 trang 99 SGK Hình học 12
Bài tập 4 trang 99 SGK Hình học 12
Bài tập 5 trang 99 SGK Hình học 12
Bài tập 6 trang 100 SGK Hình học 12
Bài tập 7 trang 100 SGK Hình học 12
Bài tập 8 trang 100 SGK Hình học 12
Bài tập 9 trang 100 SGK Hình học 12
Bài tập 10 trang 100 SGK Hình học 12
Bài tập 11 trang 101 SGK Hình học 12
Bài tập 12 trang 101 SGK Hình học 12
Bài tập 13 trang 101 SGK Hình học 12
Bài tập 14 trang 101 SGK Hình học 12
Bài tập 15 trang 101 SGK Hình học 12
Bài tập 16 trang 102 SGK Hình học 12
Bài tập 1 trang 122 SGK Hình học 12 NC
Bài tập 2 trang 122 SGK Hình học 12 NC
Bài tập 3 trang 122 SGK Hình học 12 NC
Bài tập 4 trang 122 SGK Hình học 12 NC
Bài tập 5 trang 122 SGK Hình học 12 NC
Bài tập 6 trang 123 SGK Hình học 12 NC
Bài tập 7 trang 123 SGK Hình học 12 NC
Bài tập 8 trang 123 SGK Hình học 12 NC
Bài tập 9 trang 123 SGK Hình học 12 NC
Bài tập 10 trang 123 SGK Hình học 12 NC
Bài tập 1 trang 127 SGK Hình học 12 NC
Bài tập 2 trang 127 SGK Hình học 12 NC
Bài tập 3 trang 127 SGK Hình học 12 NC
Bài tập 4 trang 128 SGK Hình học 12 NC
Bài tập 5 trang 128 SGK Hình học 12 NC
Bài tập 6 trang 128 SGK Hình học 12 NC
Bài tập 7 trang 128 SGK Hình học 12 NC
Bài tập 8 trang 129 SGK Hình học 12 NC
Bài tập 9 trang 129 SGK Hình học 12 NC
Bài tập 10 trang 129 SGK Hình học 12 NC
Bài tập 12 trang 129 SGK Hình học 12 NC
Bài tập 11 trang 129 SGK Hình học 12 NC
Bài tập 13 trang 129 SGK Hình học 12 NC
Bài tập 14 trang 130 SGK Hình học 12 NC
Bài tập 15 trang 130 SGK Hình học 12 NC
Bài tập 16 trang 130 SGK Hình học 12 NC
Bài tập 17 trang 130 SGK Hình học 12 NC
Bài tập 18 trang 130 SGK Hình học 12 NC
Bài tập 19 trang 131 SGK Hình học 12 NC
Bài tập 21 trang 131 SGK Hình học 12 NC
Bài tập 22 trang 131 SGK Hình học 12 NC
Bài tập 23 trang 132 SGK Hình học 12 NC
Bài tập 1 trang 168 SBT Hình học Toán 12
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 4 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12
-


Cho hình lăng trụ \(ABC.\,A'B'C'\) có thể tích bằng \(V\). Gọi \(M\) là trung điểm cạnh \(BB'\), điểm \(N\) thuộc cạnh \(CC'\) sao cho \(CN = 2C'N\). Hãy tính thể tích khối chóp \(A.\,BCNM\) theo \(V\).
bởi Nguyen Phuc
 07/07/2022
07/07/2022
A \({V_{A.BCNM}} = \dfrac{{7V}}{{12}}\).
B \({V_{A.BCNM}} = \dfrac{{7V}}{{18}}\).
C \({V_{A.BCNM}} = \dfrac{V}{3}\).
D \({V_{A.BCNM}} = \dfrac{{5V}}{{18}}\).
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.\,ABC\) có \(SA\) vuông góc với đáy. Tam giác \(ABC\) vuông cân tại \(B\), biết rằng \(SA = AC = 2a\). Thể tích khối chóp \(S.ABC\) là
bởi Phí Phương
 08/07/2022
08/07/2022
A. \({V_{S.\,ABC}} = \dfrac{2}{3}{a^3}.\)
B. \({V_{S.\,ABC}} = \dfrac{{{a^3}}}{3}\).
C. \({V_{S.\,ABC}} = 2{a^3}\).
D. \({V_{S.\,ABC}} = \dfrac{{4{a^3}}}{3}\).
Theo dõi (0) 1 Trả lời -


Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật \(ABCD\) có \(AB\) và \(CD\) thuộc hai đáy của hình trụ, \(AB = 4a\),\(AC = 5a\). Tính thể tích khối trụ:
bởi Ánh tuyết
 07/07/2022
07/07/2022
A \(V = 16\pi {a^3}\).
B \(V = 4\pi {a^3}\).
C \(V = 12\pi {a^3}\).
D \(V = 8\pi {a^3}\).
Theo dõi (0) 1 Trả lời -


Trong không gian Oxyz, cho hai điểm là A(2;-4;3) và B(2;2;7). Trung điểm của đoạn thẳng AB có tọa độ là
bởi Mai Vi
 16/05/2022
Theo dõi (0) 1 Trả lời
16/05/2022
Theo dõi (0) 1 Trả lời -
ADMICRO


Trong không gian \(Oxyz\), cho mặt cầu \((S):{\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 2\). Hãy xác định tọa độ tâm của mặt cầu \(\left( S \right)\).
bởi Hữu Trí
 16/05/2022
Theo dõi (0) 1 Trả lời
16/05/2022
Theo dõi (0) 1 Trả lời -


Trong không gian \(Oxyz\) cho \(A\left( {1; - 1;2} \right)\), \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = 3\end{array} \right.\), \(C\left( {0;1; - 2} \right)\). Gọi \(M\left( {a;b;c} \right)\) là điểm thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho biểu thức \(S = \overrightarrow {MA} .\overrightarrow {MB} + 2\overrightarrow {MB} .\overrightarrow {MC} + 3\overrightarrow {MC} .\overrightarrow {MA} \) đạt giá trị nhỏ nhất. Khi đó \(T = 12a + 12b + c\) có giá trị là
bởi Đào Lê Hương Quỳnh
 16/05/2022
Theo dõi (0) 1 Trả lời
16/05/2022
Theo dõi (0) 1 Trả lời -


Cho tứ diện \(ABCD\)có các cạnh \(AB,AC\)và \(AD\) đôi một vuông góc với nhau. Gọi \({G_1},{G_2},{G_3}\)và \({G_4}\) lần lượt là trọng tâm các tam giác \(ABC,ABD,ACD\)và \(BCD\). Biết \(AB = 6a,\)\(AC = 9a\), \(AD = 12a\). Hãy tính theo a thể tích khối tứ diện \({G_1}{G_2}{G_3}{G_4}\).
bởi thi trang
 16/05/2022
Theo dõi (0) 1 Trả lời
16/05/2022
Theo dõi (0) 1 Trả lời -


Cho hình chóp đều S.ABCD có cạnh đáy bằng \(a\) và cạnh bên tạo với mặt đáy một góc \(60^o\). Hãy tính thể tích của khối chóp S.ABCD ?
bởi thu hảo
 16/05/2022
Theo dõi (0) 1 Trả lời
16/05/2022
Theo dõi (0) 1 Trả lời -


Cho hình trụ có bán kính \(R\) và chiều cao\(\sqrt 3 R\). Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục d của hình trụ bằng \({30^0}\). Hãy tính khoảng cách giữa AB và trục của hình trụ.
bởi Huong Hoa Hồng
 16/05/2022
Theo dõi (0) 1 Trả lời
16/05/2022
Theo dõi (0) 1 Trả lời -


Cho hình chóp có đáy là tam giác đều cạnh cạnh bên vuông góc với đáy và thể tích của khối chóp đó bằng \(\frac{{{a^3}}}{4}\). Hãy tính cạnh bên
bởi Huong Hoa Hồng
 16/05/2022
Theo dõi (0) 1 Trả lời
16/05/2022
Theo dõi (0) 1 Trả lời -


Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm\(A'\) trên cạnh SA sao cho \(SA' = \dfrac{1}{3}SA\). Mặt phẳng qua \(A'\) và song song với đáy của hình chóp cắt các cạnh SB, SC, SD lần lượt tại B’, C’, D’. Hãy tính theo V thể tích khối chóp S.A’B’C’D’ ?
bởi Lan Ha
 16/05/2022
Theo dõi (0) 1 Trả lời
16/05/2022
Theo dõi (0) 1 Trả lời -


Hãy tính tổng các hệ số trong khai triển \({\left( {1 - 2x} \right)^{2019}}\).
bởi Hoa Lan
 15/05/2022
Theo dõi (0) 1 Trả lời
15/05/2022
Theo dõi (0) 1 Trả lời


.PNG)

