CûÀc däÀng toûÀn liûˆn quan áä¢n méˋ vû lûÇgarit trong chó¯óÀng trû˜nh phã thûÇng chÃ£Ï yä¢u áûýi hãi khÃ¤È náng ghi nhã cûÇng thãˋc vû väÙn dãËng linh hoäÀt cûÀc phó¯óÀng phûÀp giäÈi lû cû° thã xã٠lû§ häÏu hä¢t cûÀc bû i täÙp t㨠cóÀ bäÈn áä¢n nûÂng cao, khûÇng cäÏn khÃ¤È náng tó¯ duy hay suy luäÙn quûÀ phãˋc täÀp. Bû i ûÇn täÙp chó¯óÀng Hû m sã léˋy thã¨a, Hû m sã méˋ vû hû m sã lûÇgarit sä§ giû¤p cûÀc em hã thãng hû°a läÀi kiä¢n thãˋc áûÈ hãc áã ghi nhã vû väÙn dãËng tãt hóÀn vû o viãc giäÈi bû i täÙp.
Tû°m tä₤t lû§ thuyä¢t
2.1. CûÇng thãˋc méˋ vû léˋy thã¨a
Cho a vû b>0, m vû n lû nhã₤ng sã thãÝc tû¿y û§, ta cû° cûÀc cûÇng thãˋc méˋ vû léˋy thã¨a sau:
.png)
2.2. CûÇng thãˋc lûÇgarit
Cho \(a<0\ne1,b>0\) vû \(x,y>0,\) ta cû° cûÀc cûÇng thãˋc sau:
(1).png)
CûÇng thãˋc áãi cóÀ sã:
.png)
2.3. áäÀo hû m cãÏa hû m sã léˋy thã¨a, hû m sã méˋ vû hû m sã lûÇgarit
.png)
2.4. Hû m sã léˋy thã¨a, hû m sã méˋ, hû m sã lûÇgarit
a) Hû m sã léˋy thã¨a
BäÈng tû°m tä₤t cûÀc tûÙnh chäËt cãÏa hû m sã léˋy thã¨a \(y=x^{\alpha}\) trûˆn khoäÈng \(\left( {0; + \infty } \right)\)
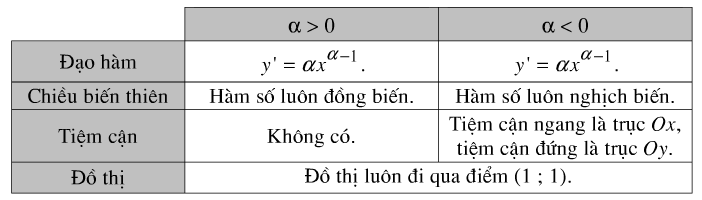
b) Hû m sã méˋ
BäÈng tû°m tä₤t cûÀc tûÙnh chäËt cãÏa hû m sã méˋ \(y=a^x(a>0,a\ne1)\)

c) Hû m sã lûÇgarit
BäÈng tû°m tä₤t cûÀc tûÙnh chäËt cãÏa hû m sã lûÇgarit \(y={\log_a}x(a>0,a\ne1)\)

2.5. Phó¯óÀng trû˜nh vû bäËt phó¯óÀng trû˜nh méˋ
- CûÀc phó¯óÀng phûÀp giäÈi:
+ Phó¯óÀng phûÀp áó¯a vã cû¿ng cóÀ sã.
+ Phó¯óÀng phûÀp lûÇgarit hû°a.
+ Phó¯óÀng phûÀp áäñt äˋn phãË.
+ Phó¯óÀng phûÀp hû m sã.
2.6. Phó¯óÀng trû˜nh vû bäËt phó¯óÀng trû˜nh lûÇgarit
- CûÀc phó¯óÀng phûÀp giäÈi:
+ Phó¯óÀng phûÀp áó¯a vã cû¿ng cóÀ sã
+ Phó¯óÀng phûÀp méˋ hû°a.
+ Phó¯óÀng phûÀp áäñt äˋn phãË.
Phó¯óÀng phûÀp hû m sã.
Bû i täÙp minh hãa
Bû i täÙp 1:
Cho a,b,c>0; a,b,c\(\neq\)1 thãa mûÈn ac = b2. CMR: \(\log_ab+\log_cb=2\log_ab.\log_cb.\)
Lãi giäÈi:
\(ac=b^2\Rightarrow \log_b\ a+\log_b\ c=2\)\(\Rightarrow \frac{1}{\log_a \ b}+\frac{1}{\log_c \ b}=2\)
\(\Rightarrow \frac{\log_c \ b +\log_a \ b}{\log_a \ b .\log_c \ b}=2\)\(\Rightarrow \log_c \ b +\log_a \ b = 2\log_a \ b . \log_c \ b\).
Bû i täÙp 2:
Cho \(\log_{3}5=a\). TûÙnh \(\log_{75}45\) theo a.
Lãi giäÈi:
\(\log_{75}45=\frac{\log_{3}45}{\log_{3}75}=\frac{\log_{3}(3^{2}.5)}{\log_{3}(3.5^{2})}\)\(=\frac{log_{3}3^{2}+log_{3}5}{log_{3}3+log_{3}5^{2}}=\frac{2+log_{3}5}{1+2log_{3}5}\)\(=\frac{2+a}{1+2a}\).
Bû i täÙp 3:
Mãt ngó¯Ã£i gãÙi tiä¢t kiãm ngûÂn hû ng vãi lûÈi suäËt 6,8%/nám vû lûÈi hû ng nám áó¯Ã£Èc nhäÙp vû o vãn. Cho biä¢t sã tiãn cÃ¤È gãc vû lûÈi áó¯Ã£Èc tûÙnh theo cûÇng thãˋc \(T=A(1+r)^n\), trong áû° A lû sã tiãn gãÙi, r lû lûÈi suäËt vû n lû sã kã° häÀn gãÙi. Hãi sau bao nhiûˆu nám ngó¯Ã£i áû° thu áó¯Ã£Èc gäËp áûÇi sã tiãn ban áäÏu?
Lãi giäÈi:
Sau n nám sã tiãn thu áó¯Ã£Èc lû \(T=A(1+0,068)^n\)
áã T = 2A thû˜ phäÈi cû° \((1,068)^n=2 \ \ (hay \ (1+6,8\%)^n=2)\)
\(\Leftrightarrow n=log_{1,068}.2\approx 10,54\)
VäÙy muãn thu áó¯Ã£Èc gäËp áûÇi sã tiãn ban áäÏu, ngó¯Ã£i áû° phäÈi gãÙi 11 nám.
Bû i täÙp 4:
GiäÈi phó¯óÀng trû˜nh \(\log_8\frac{8}{x^2}=3\log_8^2x.\)
Lãi giäÈi:
áiãu kiãn: \(\left\{ \begin{array}{l}
x > 0\\
{\log _8}\frac{8}{{{x^2}}} \ge 0
\end{array} \right. \Leftrightarrow 0 < x < 2\sqrt 2 .\)
\(\log_8\frac{8}{x^2}=3\log_8^2x\Leftrightarrow \log_88 -\log_8x^2=3.\log_8^2x\)
\(\Leftrightarrow 3\log_8^2x+2\log_8x^2-1=0\)
áäñt \(t=\log_8x\), phó¯óÀng trû˜nh trã thû nh: \(3{t^2} + 2t - 1 = 0 \Leftrightarrow \left[ \begin{array}{l} t = - 1\\ t = \frac{1}{3} \end{array} \right.\)
Vãi: \(t=-1\Leftrightarrow log_8x=-1\Leftrightarrow x=\frac{1}{8}\)
Vãi: \(t=\frac{1}{3}\Leftrightarrow log_8x=\frac{1}{3}\Leftrightarrow x=2\)
VäÙy täÙp nghiãm phó¯óÀng trû˜nh lû : \(\left \{ \frac{1}{8};2 \right \}\).
Bû i täÙp 5:
GiäÈi bäËt phó¯óÀng trû˜nh: \(\log_{0,5}x+2\log_{0,25}(x-1)+\log_26\geq 0.\)
Lãi giäÈi:
áiãu kiãn: x> 1 (*).
Khi áû° ta cû°:
\(\log_{0,5}x+2\log_{0,25}(x-1)+\log_26\geq 0\)
\(\Leftrightarrow \log_2x-\log_2(x-1)+\log_26\geq 0\)
\(\Leftrightarrow \log_2[x(x-1)]\leq \log_26\Leftrightarrow x(x-1)\leq 6\Leftrightarrow x^2-x-6\leq 0\)
\(\Leftrightarrow -2\leq x\leq 3\).
Kä¢t hãÈp áiãu kiãn (*) ta áó¯Ã£Èc \(1 < x \le 3\)
VäÙy täÙp nghiãm bäËt phó¯óÀng trû˜nh lû S=(1;3].
Bû i täÙp 6:
GiäÈi phó¯óÀng trû˜nh \(27^x-5.3^{2-3x}=4.\)
Lãi giäÈi:
\(27^x-5.3^{2-3x}=4\Leftrightarrow 27^x-\frac{45}{27^x}=4\Leftrightarrow (27^x)^2-4.27^x-45=0\)
áäñt: \(t=27^x(t>0)\) ta áó¯Ã£Èc \(t^2-4t-45=0\)\(\Leftrightarrow t=9\) (Do t>0).
\(\Rightarrow 3^{3x}=3^2\Leftrightarrow 3x=2\Leftrightarrow x=\frac{2}{3}\).
VäÙy phó¯óÀng trû˜nh áûÈ cho cû° nghiãm lû \(x=\frac{2}{3}\).
Bû i täÙp 7:
GiäÈi bäËt phó¯óÀng trû˜nh \(4^x-3^x>1.\)
Lãi giäÈi:
\(4^x-3^x>1\Leftrightarrow 4^x>3^x+1\)\(\Leftrightarrow 1>(\frac{3}{4})^x+(\frac{1}{4})^x\)
Vãi \(x\leq 1\) ta cû°: \(\left.\begin{matrix} \left ( \frac{3}{4} \right )^x\geqslant \frac{3}{4}\\ \\ \left ( \frac{1}{4} \right )^x\geqslant \frac{1}{4} \end{matrix}\right\}VP\geqslant 1\) KhûÇng thãa mûÈn.
Vãi \(x>1\) ta cû°: \(\left.\begin{matrix} (\frac{3}{4})^x<\frac{3}{4}\\ \\ (\frac{1}{4})^x< \frac{1}{4} \end{matrix}\right\}VP< 1\) thãa mûÈn.
VäÙy bäËt phó¯óÀng trû˜nh cû° täÙp nghiãm lû : \(S=(1;+\infty ).\)
4. Luyãn täÙp ûn täÙp Chó¯óÀng 2 ToûÀn 12
CûÀc däÀng toûÀn liûˆn quan áä¢n méˋ vû lûÇgarit trong chó¯óÀng trû˜nh phã thûÇng chÃ£Ï yä¢u áûýi hãi khÃ¤È náng ghi nhã cûÇng thãˋc vû väÙn dãËng linh hoäÀt cûÀc phó¯óÀng phûÀp giäÈi lû cû° thã xã٠lû§ häÏu hä¢t cûÀc bû i täÙp t㨠cóÀ bäÈn áä¢n nûÂng cao, khûÇng cäÏn khÃ¤È náng tó¯ duy hay suy luäÙn quûÀ phãˋc täÀp. Bû i ûÇn täÙp chó¯óÀng Hû m sã léˋy thã¨a, Hû m sã méˋ vû hû m sã lûÇgarit sä§ giû¤p cûÀc em hã thãng hû°a läÀi kiä¢n thãˋc áûÈ hãc áã ghi nhã vû väÙn dãËng tãt hóÀn vû o viãc giäÈi bû i täÙp.
4.1 Trä₤c nghiãm
áã cãÏng cã bû i hãc xin mãi cûÀc em cû¿ng lû m Bû i kiãm tra Trä₤c nghiãm ToûÀn 12 ûn täÙp chó¯óÀng 2 áã kiãm tra xem mû˜nh áûÈ nä₤m áó¯Ã£Èc nãi dung bû i hãc hay chó¯a.
-
- A. \(P = {x^{\frac{{14}}{{15}}}}\)
- B. \(P = {x^{\frac{{17}}{{36}}}}\)
- C. \(P = {x^{\frac{{13}}{{15}}}}\)
- D. \(P = {x^{\frac{{16}}{{15}}}}\)
-
- A. \(x=5\)
- B. \(x=4\)
- C. \(x=6\)
- D. \(x=17\)
-
- A. \(x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
- B. \(x \in (-2;0)\)
- C. \(x \in (0;2)\)
- D. \(x \in \left( { - \infty ; - 2} \right) \cup \left( {0; + \infty } \right)\)
CûÂu 4-10: Mãi cûÀc em ááng nhäÙp xem tiä¢p nãi dung vû thi thã٠Online áã cãÏng cã kiä¢n thãˋc vû nä₤m vã₤ng hóÀn vã bû i hãc nû y nhûˋ!
4.2 Bû i täÙp SGK
Bûˆn cäÀnh áû° cûÀc em cû° thã xem phäÏn hó¯Ã£ng dä¨n GiäÈi bû i täÙp ToûÀn 12 ûn täÙp chó¯óÀng 2 sä§ giû¤p cûÀc em nä₤m áó¯Ã£Èc cûÀc phó¯óÀng phûÀp giäÈi bû i täÙp t㨠SGK GiäÈi tûÙch 12 CóÀ bäÈn vû NûÂng cao.
Bû i täÙp 1 trang 90 SGK GiäÈi tûÙch 12
Bû i täÙp 2 trang 90 SGK GiäÈi tûÙch 12
Bû i täÙp 3 trang 90 SGK GiäÈi tûÙch 12
Bû i täÙp 4 trang 90 SGK GiäÈi tûÙch 12
Bû i täÙp 5 trang 90 SGK GiäÈi tûÙch 12
Bû i täÙp 6 trang 90 SGK GiäÈi tûÙch 12
Bû i täÙp 7 trang 90 SGK GiäÈi tûÙch 12
Bû i täÙp 8 trang 90 SGK GiäÈi tûÙch 12
Bû i täÙp 1 trang 91 SGK GiäÈi tûÙch 12
Bû i täÙp 2 trang 91 SGK GiäÈi tûÙch 12
Bû i täÙp 3 trang 91 SGK GiäÈi tûÙch 12
Bû i täÙp 4 trang 91 SGK GiäÈi tûÙch 12
Bû i täÙp 5 trang 91 SGK GiäÈi tûÙch 12
Bû i täÙp 6 trang 91 SGK GiäÈi tûÙch 12
Bû i täÙp 7 trang 91 SGK GiäÈi tûÙch 12
Bû i täÙp 2.65 trang 133 SBT ToûÀn 12
Bû i täÙp 2.66 trang 133 SBT ToûÀn 12
Bû i täÙp 2.67 trang 133 SBT ToûÀn 12
Bû i täÙp 2.68 trang 133 SBT ToûÀn 12
Bû i täÙp 2.69 trang 133 SBT ToûÀn 12
Bû i täÙp 2.70 trang 133 SBT ToûÀn 12
Bû i täÙp 2.71 trang 134 SBT ToûÀn 12
Bû i täÙp 2.72 trang 134 SBT ToûÀn 12
Bû i täÙp 2.73 trang 134 SBT ToûÀn 12
Bû i täÙp 2.74 trang 134 SBT ToûÀn 12
Bû i täÙp 2.75 trang 134 SBT ToûÀn 12
Bû i täÙp 2.76 trang 134 SBT ToûÀn 12
Bû i täÙp 2.77 trang 134 SBT ToûÀn 12
Bû i täÙp 2.78 trang 135 SBT ToûÀn 12
Bû i täÙp 2.79 trang 135 SBT ToûÀn 12
Bû i täÙp 2.80 trang 135 SBT ToûÀn 12
Bû i täÙp 2.81 trang 135 SBT ToûÀn 12
Bû i täÙp 2.82 trang 135 SBT ToûÀn 12
Bû i täÙp 2.83 trang 135 SBT ToûÀn 12
Bû i täÙp 2.84 trang 135 SBT ToûÀn 12
Bû i täÙp 2.85 trang 135 SBT ToûÀn 12
Bû i täÙp 2.86 trang 135 SBT ToûÀn 12
Bû i täÙp 2.87 trang 135 SBT ToûÀn 12
Bû i täÙp 2.88 trang 136 SBT ToûÀn 12
Bû i täÙp 2.89 trang 136 SBT ToûÀn 12
Bû i täÙp 2.90 trang 136 SBT ToûÀn 12
Bû i täÙp 2.91 trang 136 SBT ToûÀn 12
Bû i täÙp 2.92 trang 136 SBT ToûÀn 12
Bû i täÙp 2.93 trang 136 SBT ToûÀn 12
Bû i täÙp 2.94 trang 136 SBT ToûÀn 12
Bû i täÙp 2.95 trang 136 SBT ToûÀn 12
Bû i täÙp 2.96 trang 136 SBT ToûÀn 12
Bû i täÙp 2.97 trang 137 SBT ToûÀn 12
Bû i täÙp 2.98 trang 137 SBT ToûÀn 12
Bû i täÙp 2.99 trang 137 SBT ToûÀn 12
Bû i täÙp 2.100 trang 137 SBT ToûÀn 12
Bû i täÙp 2.101 trang 137 SBT ToûÀn 12
Bû i täÙp 2.102 trang 137 SBT ToûÀn 12
Bû i täÙp 2.103 trang 137 SBT ToûÀn 12
Bû i täÙp 2.104 trang 137 SBT ToûÀn 12
Bû i täÙp 2.105 trang 137 SBT ToûÀn 12
Bû i täÙp 84 trang 130 SGK ToûÀn 12 NC
Bû i täÙp 85 trang 130 SGK ToûÀn 12 NC
Bû i täÙp 86 trang 130 SGK ToûÀn 12 NC
Bû i täÙp 87 trang 130 SGK ToûÀn 12 NC
Bû i täÙp 88 trang 130 SGK ToûÀn 12 NC
Bû i täÙp 89 trang 131 SGK ToûÀn 12 NC
Bû i täÙp 90 trang 131 SGK ToûÀn 12 NC
Bû i täÙp 91 trang 131 SGK ToûÀn 12 NC
Bû i täÙp 92 trang 131 SGK ToûÀn 12 NC
Bû i täÙp 93 trang 131 SGK ToûÀn 12 NC
Bû i täÙp 94 trang 131 SGK ToûÀn 12 NC
Bû i täÙp 95 trang 132 SGK ToûÀn 12 NC
Bû i täÙp 96 trang 132 SGK ToûÀn 12 NC
Bû i täÙp 97 trang 132 SGK ToûÀn 12 NC
Bû i täÙp 98 trang 132 SGK ToûÀn 12 NC
Bû i täÙp 99 trang 132 SGK ToûÀn 12 NC
Bû i täÙp 100 trang 132 SGK ToûÀn 12 NC
Bû i täÙp 101 trang 132 SGK ToûÀn 12 NC
Bû i täÙp 102 trang 133 SGK ToûÀn 12 NC
Bû i täÙp 103 trang 133 SGK ToûÀn 12 NC
Bû i täÙp 104 trang 133 SGK ToûÀn 12 NC
Bû i täÙp 105 trang 133 SGK ToûÀn 12 NC
Bû i täÙp 106 trang 133 SGK ToûÀn 12 NC
Bû i täÙp 107 trang 133 SGK ToûÀn 12 NC
Bû i täÙp 108 trang 134 SGK ToûÀn 12 NC
Bû i täÙp 109 trang 135 SGK ToûÀn 12 NC
Bû i täÙp 110 trang 135 SGK ToûÀn 12 NC
5. Hãi áûÀp ûn täÙp Chó¯óÀng 2 ToûÀn 12
Nä¢u cû° thä₤c mä₤c cäÏn giäÈi áûÀp cûÀc em cû° thã áã läÀi cûÂu hãi trong phäÏn Hãi áûÀp, cãng áãng ToûÀn HãC247 sä§ sãm trÃ¤È lãi cho cûÀc em.
-- Mod ToûÀn Hãc 12 HãC247











