Tuy là một khái niệm mới nhưng số phức được xem là một trong những dạng toán dễ trong chương trình phổ thông. Các câu hỏi liên quan đến số phức luôn được xem là câu "ăn điểm". Bài ôn tập chương Số phức sẽ giúp các em tổng hợp lại hệ thống kiến thức đã được học trong các bài, bên cạnh đó là những bài tập tổng hợp có hướng dẫn giải sẽ giúp các em rèn luyện kĩ năng làm bài và nắm vững kiến thức hơn.
Tóm tắt lý thuyết
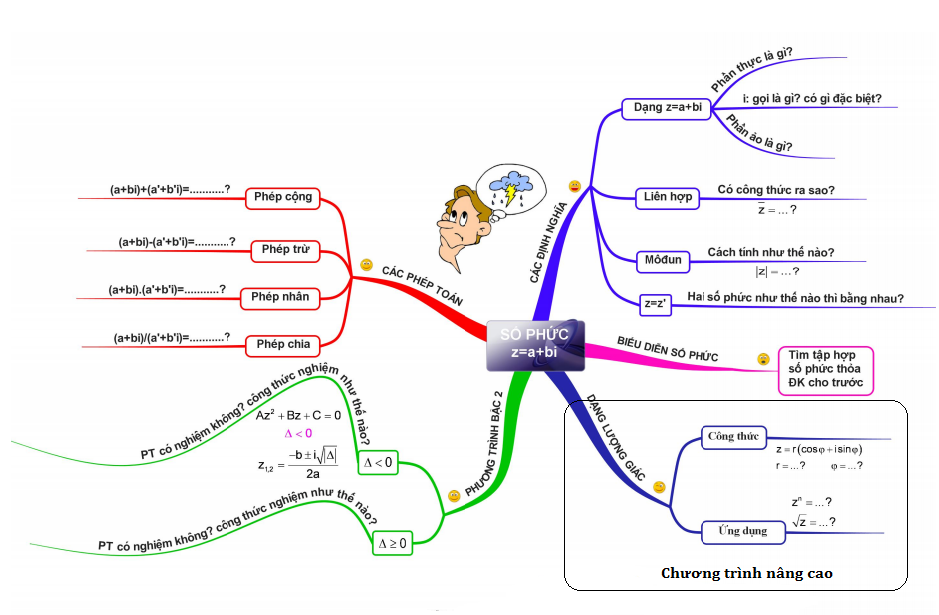
HỆ THỐNG HÓA KIẾN THỨC "SỐ PHỨC VÀ CÁC DẠNG TOÁN LIÊN QUAN"
Bài tập minh họa
Bài tập 1:
Tìm số phức z sao cho (1 +2i)z là số thuần ảo và \(\left | 2.z-\bar{z} \right |=\sqrt{13}\).
Lời giải:
Giả sử \(z=a+bi \ (a,b\in R)\).
Khi đó \((1+2i)z=(1+2i)(a+bi)=(a-2b)+(2a+b)i.\)
(1 +2i)z là số thuần ảo khi và chỉ khi: \(a-2b=0\Leftrightarrow a=2b\)
\(\left | 2.z-\bar{z} \right |=\left | a+3bi \right |=\left | 2b+3bi \right | =\sqrt{13b^2}=\sqrt{13}\Leftrightarrow b=\pm 1.\)
Vậy có hai số phức thỏa mãn đề bài: \(z=2+i;z=-2-i.\)
Bài tập 2:
Tìm phần thực và phần ảo của số phức z thoả mãn điều kiện \(z+(2+i)\bar{z}=3+5i.\)
Lời giải:
Giả sử \(z=a+bi(a,b\in R)\)
Ta có
\(z+(1+i)\bar{z}=3+5i\Leftrightarrow a+bi+(2+i)(a-bi)=3+5i\)
\(\Leftrightarrow 3a+b+(a-b)i=3+5i\)
\(\Leftrightarrow \left\{\begin{matrix} 3a+b=3\\ a-b=5 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=2\\ b=-3 \end{matrix}\right.\)
Vậy z=2-3i.
Do đó phần thực của z là 2 và phần ảo của z là –3.
Bài tập 3:
Cho hai số phức \(z_1,z_2\) thỏa mãn \(\left |z_1 \right |=\left |z_2 \right |=1,\left |z_1 +z_2 \right | =\sqrt{3}\). Tính \(\left |z_1 -z_2 \right |.\)
Lời giải:
Đặt: \(z_1=a_1+b_1i;z_2=a_2+b_2i \ (a_1,a_2,b_1,b_2 \in R)\)
\(\left\{\begin{matrix} \left | z_1 \right | =\left | z_2 \right |=1\\ \left | z_1 +z_2\right |=\sqrt{3} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} a^2_1+b^2_1=a^2_2+b^2_2=1\\ (a_1+b_2)^2+(b_1+b_2)^2=2 \end{matrix}\right.\)
\(\Leftrightarrow 2(a_1b_1+a_2b_2)=1\Rightarrow (a_1-a_2)^2+(b_1-b_2)^2=1\)
Vậy \(\left | z_1-z_2 \right |=1.\)
Bài tập 4:
Cho số phức z thỏa mãn điều kiện \((1+2i)z+(3+2i)\bar{z}=4+10i.\) Tìm môđun của số phức \(w=z+2\bar{z}.\)
Lời giải:
Đặt \(z=a+bi(a,b\in R)\Rightarrow \bar{z}=a-bi\)
Ta có \((1+2i)z+(3+2i)\bar{z}=4+10i\)
\(\Leftrightarrow (1+2i)(a+bi)+(3+2i)(a-bi)(a-bi)=4+10i\)
\(\Leftrightarrow 4a+(4a-2b)i=4+10i\Leftrightarrow \left\{\begin{matrix} 4a=4\\ 4a-2b=10 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=1\\ b=-3 \end{matrix}\right.\)
Do đó \(z= 1- 3i.\)
Ta có: \(w=z+2\bar{z}=1-3i+2(1+3i)=3+3i.\)
Suy ra môđun của w là \(\left | w \right |=\sqrt{3^2+3^2}=3\sqrt{2}.\)
4. Luyện tập Ôn tập Chương 4 Toán 12
Tuy là một khái niệm mới nhưng số phức được xem là một trong những dạng toán dễ trong chương trình phổ thông. Các câu hỏi liên quan đến số phức luôn được xem là câu "ăn điểm". Bài ôn tập chương Số phức sẽ giúp các em tổng hợp lại hệ thống kiến thức đã được học trong các bài, bên cạnh đó là những bài tập tổng hợp có hướng dẫn giải sẽ giúp các em rèn luyện kĩ năng làm bài và nắm vững kiến thức hơn.
4.1 Trắc nghiệm
Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Ôn tập chương IV - Toán 12 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. Đường tròn\({(x - 1)^2} + {(y - 4)^2} = 125\)
- B. Đường tròn \({(x - 5)^2} + {(y - 4)^2} = 125\)
- C. Đường tròn \({(x +1)^2} + {(y - 2)^2} = 125\)
- D. Đường thẳng x=2
-
- A. z=7+8i
- B. z=5+2i
- C. z=-3
- D. z=-3+8i
-
- A. P=-14
- B. P=14
- C. P=-14i
- D. P=14i
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
4.2 Bài tập SGK
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Ôn tập chương IV - Toán 12 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Giải tích 12 Cơ bản và Nâng cao.
Bài tập 1 trang 143 SGK Giải tích 12
Bài tập 2 trang 143 SGK Giải tích 12
Bài tập 3 trang 143 SGK Giải tích 12
Bài tập 4 trang 143 SGK Giải tích 12
Bài tập 5 trang 143 SGK Giải tích 12
Bài tập 6 trang 143 SGK Giải tích 12
Bài tập 7 trang 143 SGK Giải tích 12
Bài tập 8 trang 143 SGK Giải tích 12
Bài tập 9 trang 144 SGK Giải tích 12
Bài tập 10 trang 144 SGK Giải tích 12
Bài tập 11 trang 144 SGK Giải tích 12
Bài tập 12 trang 144 SGK Giải tích 12
Bài tập 1 trang 144 SGK Giải tích 12
Bài tập 2 trang 144 SGK Giải tích 12
Bài tập 3 trang 144 SGK Giải tích 12
Bài tập 4 trang 144 SGK Giải tích 12
Bài tập 5 trang 144 SGK Giải tích 12
Bài tập 6 trang 144 SGK Giải tích 12
Bài tập 4.35 trang 207 SBT Toán 12
Bài tập 3.36 trang 207 SBT Toán 12
Bài tập 4.37 trang 208 SBT Toán 12
Bài tập 4.38 trang 208 SBT Toán 12
Bài tập 4.39 trang 208 SBT Toán 12
Bài tập 4.40 trang 208 SBT Toán 12
Bài tập 4.41 trang 208 SBT Toán 12
Bài tập 4.42 trang 208 SBT Toán 12
Bài tập 4.47 trang 209 SBT Toán 12
Bài tập 4.43 trang 208 SBT Toán 12
Bài tập 4.44 trang 208 SBT Toán 12
Bài tập 4.45 trang 208 SBT Toán 12
Bài tập 4.46 trang 209 SBT Toán 12
Bài tập 4.48 trang 209 SBT Toán 12
Bài tập 4.49 trang 209 SBT Toán 12
Bài tập 37 trang 208 SGK Toán 12 NC
Bài tập 38 trang 209 SGK Toán 12 NC
Bài tập 39 trang 209 SGK Toán 12 NC
Bài tập 40 trang 209 SGK Toán 12 NC
Bài tập 41 trang 209 SGK Toán 12 NC
Bài tập 42 trang 209 SGK Toán 12 NC
Bài tập 43 trang 210 SGK Toán 12 NC
Bài tập 44 trang 210 SGK Toán 12 NC
Bài tập 45 trang 210 SGK Toán 12 NC
Bài tập 46 trang 210 SGK Toán 12 NC
Bài tập 47 trang 210 SGK Toán 12 NC
Bài tập 48 trang 210 SGK Toán 12 NC
Bài tập 49 trang 210 SGK Toán 12 NC
Bài tập 50 trang 210 SGK Toán 12 NC
Bài tập 51 trang 210 SGK Toán 12 NC
Bài tập 52 trang 210 SGK Toán 12 NC
Bài tập 53 trang 211 SGK Toán 12 NC
Bài tập 54 trang 211 SGK Toán 12 NC
5. Hỏi đáp Ôn tập Chương 4 Toán 12
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.
-- Mod Toán Học 12 HỌC247







