Bài tập 42 trang 209 SGK Toán 12 NC
a.
Bằng cách biểu diễn hình học các số phức 2 + i và 3 + i, hãy chứng minh rằng nếu \(\tan a = {1 \over 2},\,\tan b = {1 \over 3}\)với \(a,b \in \left( {0;{\pi \over 2}} \right)\) thì \(a + b = {\pi \over 4}\).
b.
Bằng cách biển diễn hình học các số phức 2 + i, 5+ i và 8 + i, hãy chứng minh rằng nếu \(\tan a = {1 \over 2},\,\tan b = {1 \over 5},\,\tan c = {1 \over 8}\) với \(a,b,c \in \left( {0;{\pi \over 2}} \right)\) thì \(a + b + c = {\pi \over 4}\).
Hướng dẫn giải chi tiết
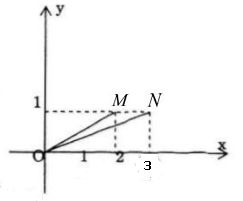
a.
Biểu diễn hình học \(2 + i, 3 + i\) theo thứ tự bới M và N trong mặt phẳng phức
Ta có: \(\tan \left( {Ox,\,OM} \right) = {1 \over 2} = \tan a\)
\(\tan \left( {Ox,\,ON} \right) = {1 \over 3} = \tan b\)
Xét \(z.z' = (2 + i).(3 + i) = 5(1 + i) \)
\(= 5\sqrt 2 \left( {\cos {\pi \over 4} + i\sin {\pi \over 4}} \right)\)
Số \(zz'\) có acgumen là \({{\pi \over 4}}\).
Mà zz' cũng có acgumen là a+b.
Suy ra \(a + b = {\pi \over 4}\)
b.
\({z_1} = 2 + i\) có một acgumen là a với \(\tan a = {1 \over 2}\)
\({z_2} = 5 + i\) có một acgumen là b với \(\tan b = {1 \over 5}\)
\({z_3} = 8 + i\) có một acgumen là c với \(\tan c = {1 \over 8}\)
Xét \(z = {z_1}{z_2}{z_3} = \left( {2 + i} \right)\left( {5 + i} \right)\left( {8 + i} \right) \) \(= 65\left( {1 + i} \right)\)
\(= 65\sqrt 2 \left( {{{\sqrt 2 } \over 2} + i{{\sqrt 2 } \over 2}} \right) \) \(= 65\sqrt 2 \left( {\cos {\pi \over 4} + i\sin {\pi \over 4}} \right)\)
\(z\) có acgumen là \({\pi \over 4}\), suy ra \(a + b + c = {\pi \over 4}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 40 trang 209 SGK Toán 12 NC
Bài tập 41 trang 209 SGK Toán 12 NC
Bài tập 43 trang 210 SGK Toán 12 NC
Bài tập 44 trang 210 SGK Toán 12 NC
Bài tập 45 trang 210 SGK Toán 12 NC
Bài tập 46 trang 210 SGK Toán 12 NC
Bài tập 47 trang 210 SGK Toán 12 NC
Bài tập 48 trang 210 SGK Toán 12 NC
Bài tập 49 trang 210 SGK Toán 12 NC
Bài tập 50 trang 210 SGK Toán 12 NC
Bài tập 51 trang 210 SGK Toán 12 NC
Bài tập 52 trang 210 SGK Toán 12 NC
-


cho ptrinh z2 +bz + c có 1 nghiệm là z=1-2i tìm bc
Theo dõi (0) 7 Trả lời -


Tìm P=8(b^2-a^2)-12 theo |z| biết z thỏa |z^2+4|=2|z
bởi Lê Văn Duyệt
 24/10/2018
24/10/2018
Z=a+bi (a,b thuộc R) thoả |z^2+4|=2|z| Đặt P=8(b^2-a^2)-12 tìm P theo |z|
Theo dõi (0) 1 Trả lời -


Tính mô đun của số phức w=1-z+z^2
bởi bach dang
 24/10/2018
24/10/2018
cho số phức z có phần thực là số nguyên và z thõa mãn \(_{\left|z\right|-2\overline{z}=-7+3i+z}\)tính modun của số phức w= 1-z+\(^{z_{ }^2}\)
Theo dõi (0) 1 Trả lời -


Tính P=a+b khi |z+1-3i|+||z+1+i| đạt GTLN
bởi Thùy Trang
 24/10/2018
24/10/2018
Xét các số phức z thỏa mãn |z - 4 -3i| = \(\sqrt{5}\). Tiính P= a+ b khi | z +1 -3i| + | z-1+i| đạt giá trị lớn nhất
Theo dõi (0) 1 Trả lời -
ADMICRO


Có bao nhiêu số z thỏa mãn |z+2 -i| = 2\(\sqrt{2}\) và (z-1)2 là số thuần ảo
Theo dõi (0) 2 Trả lời -


Tìm số phức z thỏa (i. z ngang+3+i)(iz+1)=0
bởi Huong Duong
 24/10/2018
24/10/2018
tìm số phức z thỏa mãn:
1. (i\(\overline{z}\) +3+i)(iz+1)=0
2.\(z^2\) -\(\overline{z}\) =0
.
Theo dõi (0) 1 Trả lời -


Tính bán kính nhỏ nhất, biết tập hợp các điểm biểu diễn w = (3-4i)z - 2i là đường tròn
bởi Đào Lê Hương Quỳnh
 24/10/2018
24/10/2018
Cho |z| = m2 + 2m + 5 với m là tham số thực. Biết rằng tập hợp các điểm biểu diễn các số phức w = (3-4i)z - 2i là một đường tròn. Tính bán kính nhỏ nhất của đường tròn đó
Theo dõi (0) 1 Trả lời



