Hướng dẫn Giải bài tập Ôn tập chương IV - Toán 12 ôn tập Số phức sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức đã học.
-
Bài tập 1 trang 143 SGK Giải tích 12
Thế nào là phần thực phần ảo, mô đun của một số phức? Viết công thức tính mô đun của số phức theo phần thực phần ảo của nó?
-
Bài tập 2 trang 143 SGK Giải tích 12
Tìm mối liên hệ giữa khái niêm môđun và khái niệm giá trị tuyệt đối của số thực.
-
Bài tập 3 trang 143 SGK Giải tích 12
Nêu định nghĩa số phức liên hợp với số phức z. Số phức nào bằng số phức liên hợp của nó?
-
Bài tập 4 trang 143 SGK Giải tích 12
Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình a, b , c?
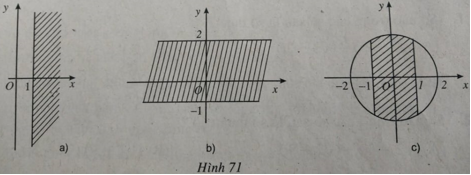
- VIDEOYOMEDIA
-
Bài tập 5 trang 143 SGK Giải tích 12
Trên mặt phẳng tọa độ, tìm tập hợp biểu diễn của các số phức z thỏa mãn điều kiện:
a) Phần thực của z bằng 1.
b) Phần ảo của z bằng -2.
c) Phần thực của z thuộc đoạn [-1; 2], phần ảo của z thuộc đoạn [0; 1].
d) \(|z|\leq 2\).
-
Bài tập 6 trang 143 SGK Giải tích 12
Tìm các số thực x, y sao cho:
\(a) \ 3x+yi=2y+1+(2-x)i\).
\(b) \ 2x+y-1=(x+2y-5)i\).
-
Bài tập 7 trang 143 SGK Giải tích 12
Chứng tỏ rằng với mọi số thực z, ta luôn phần thực và phần ảo của nó không vượt quá mô đun của nó.
-
Bài tập 8 trang 143 SGK Giải tích 12
Thực hiện các phép tính sau:
a) \((3+2i)\left [ (2-i)+(3-2i) \right ]\)
b) \((4-3i)+\frac{1+i}{2+i}\).
c) \((1+i)^2-(1-i)^2\).
d) \(\frac{3+i}{2+i}-\frac{4-3i}{2-i}\). -
Bài tập 9 trang 144 SGK Giải tích 12
Giải các phương trình sau trên tập số phức:
a) (3+4i)z + (1-3i) = 2+5i.
b) (4+7i)z - (5-2i) = 6iz.
-
Bài tập 10 trang 144 SGK Giải tích 12
Giải các phương trình sau trên tập số phức:
a) \(3z^2+7z+8=0.\)
b) \(z^4-8=0.\)
c) \(z^4-1=0.\)
-
Bài tập 11 trang 144 SGK Giải tích 12
Tìm hai số phức, biết tổng của chúng bằng 3 và tích của chúng bằng 4.
-
Bài tập 12 trang 144 SGK Giải tích 12
Cho hai số phức z1,z2, biết rằng z1+z2 và z1.z2 là hai số thực. Chứng tỏ rằng z1,z2 là hai nghiệm của một phương trình bậc hai với hệ số thực.
-
Bài tập 1 trang 144 SGK Giải tích 12
Số nào trong các số sau là số thực?
\((A)(\sqrt{3}+2i)-(\sqrt{3-2i})\)
\((B) (2+i\sqrt{5})+(2-i\sqrt{5})\)
\((C) (1+i\sqrt{3})^2\)
\((D)\frac{\sqrt{2}+i}{\sqrt{2}-i}\) -
Bài tập 2 trang 144 SGK Giải tích 12
Số nào trong các sô sau là số ảo?
\(\\ (A).(\sqrt{2}+3i)(\sqrt{2-3i}) \\ \ \ \ \ (B). (\sqrt{2}-3i)(\sqrt{2+3i}) \\ (C). (2+2i)^2 \\ (D). \frac{3+2i}{2-3i}\) -
Bài tập 3 trang 144 SGK Giải tích 12
Đẳng thức nào sau đây là đẳng thức đúng?
(A). i1977=-1
(B). i2345=i
(C). i2005=1
(D). i2006=-i
-
Bài tập 4 trang 144 SGK Giải tích 12
Đẳng thức nào trong các đẳng thức sau là đúng?
(A). (1-i)8=-16
(B). (1+i)8=16i
(C). (1+i)8=16
(D). (1+i)8=-16i
-
Bài tập 5 trang 144 SGK Giải tích 12
Biết nghịch đảo của số phức z bằng số phức liên hợp của nó, trong các kết luận sau, kết luận nào là đúng?
(A). \(z\in \mathbb{R}\)
(B). \(|z|=1\)
(C). z là số thuần ảo
(D). \(|z|=-1\)
-
Bài tập 6 trang 144 SGK Giải tích 12
Trong các kết luận sau, kết luận nào là sai?
A. Mô đun của số phức z là một số thực.
B. Mô đun của số phức z là một số phức.
C. Mô đun của số phức z là một số thực dương.
D. Mô đun của số phức z là một số thực không âm.
-
Bài tập 4.35 trang 207 SBT Toán 12
Áp dụng các hằng đẳng thức đáng nhớ để tính
a) \({{{\left( {2 + i\sqrt 3 } \right)}^2}}\)b) \({{{\left( {1 + 2i} \right)}^3}}\)
c) \({{{\left( {3 - i\sqrt 2 } \right)}^2}}\)
d) \({{{\left( {2 - i} \right)}^3}}\)
-
Bài tập 3.36 trang 207 SBT Toán 12
Giải các phương trình sau trên tập số phức :
a) \({\left( {1 + 2i} \right)x - \left( {4 - 5i} \right) = - 7 + 3i}\)b) \({\left( {3 + 2i} \right)x - 6ix = \left( {1 - 2i} \right)\left[ {x - \left( {1 + 5i} \right)} \right]}\)
-
Bài tập 4.37 trang 208 SBT Toán 12
Giải các phương trình sau trên tập số phức :
a) \({3{x^2} + \left( {3 + 2i\sqrt 2 } \right)x - \frac{{{{\left( {1 + i} \right)}^3}}}{{1 - i}} = i\sqrt 8 x}\)b) \({{{\left( {1 - ix} \right)}^2} + \left( {3 + 2i} \right)x - 5 = 0}\)
-
Bài tập 4.38 trang 208 SBT Toán 12
Tìm số phức z, biết:
a) \({\bar z = {z^3}}\)b) \({\left| z \right| + z = 3 + 4i}\)
-
Bài tập 4.39 trang 208 SBT Toán 12
Tìm số phức thỏa mãn hệ phương trình
\(\left\{ \begin{array}{l}
\left| {z - 2i} \right| = \left| z \right|\\
\left| {z - i} \right| = \left| {z - 1} \right|
\end{array} \right.\) -
Bài tập 4.40 trang 208 SBT Toán 12
Chứng tỏ rằng \(\frac{{z - 1}}{{z + 1}}\) là số thực khi và chỉ khi là một số thực khác
-
Bài tập 4.41 trang 208 SBT Toán 12
Tìm phần ảo của số phức \(z\) biết \(\overline z = {(\sqrt 2 + i)^2}(1 - i\sqrt 2 )\)
-
Bài tập 4.42 trang 208 SBT Toán 12
Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn \(\left| {z - \left( {3 - 4i} \right)} \right| = 2\)
-
Bài tập 4.47 trang 209 SBT Toán 12
Cho z là một số phức tùy ý. Mệnh đề nào sau đây sai?
A. \(z \in R \Leftrightarrow z = \bar z\)
B. z thuần ảo \( \Leftrightarrow z + \bar z = 0\)
C. \(\frac{z}{{\bar z}} - \frac{{\bar z}}{z} \in R\left( {z \ne 0} \right)\)
D. \({z^3} + {\left( {\bar z} \right)^3} \in R\)
-
Bài tập 4.43 trang 208 SBT Toán 12
Trên mặt phẳng , tìm tập hợp điểm biểu diễn các số phức thỏa mãn điều kiện \(\left| {z - i} \right| = \left| {\left( {1 + i} \right)z} \right|\)
-
Bài tập 4.44 trang 208 SBT Toán 12
Tìm số phức z, thỏa mãn : \(\left| {z - \left( {2 + i} \right)} \right| = \sqrt {10} \) và \(z.\bar z = 25\)
-
Bài tập 4.45 trang 208 SBT Toán 12
Số nào sau đây là số thực?
A. \(\frac{{2 + i\sqrt 2 }}{{1 - i\sqrt 2 }} + \frac{{1 + i\sqrt 2 }}{{2 - i\sqrt 2 }}\)
B. \(\left( {2 + 3i} \right)\left( {3 - i} \right) + \left( {2 - 3i} \right)\left( {3 + i} \right)\)
C. \(\frac{{\left( {1 + i} \right)\left( {2 + i} \right)}}{{2 - i}} + \frac{{\left( {1 + i} \right)\left( {2 - i} \right)}}{{2 + i}}\)
D. \({\left( {2 + i\sqrt 3 } \right)^2} - {\left( {2 - i\sqrt 3 } \right)^2}\)
-
Bài tập 4.46 trang 209 SBT Toán 12
Số nào sau đây là số thuần ảo ?
A. \({\frac{{{{\left( {1 + i} \right)}^5}}}{{{{\left( {1 - i} \right)}^3}}}}\)B. \({{{\left( {1 + i} \right)}^5} - {{\left( {1 - i} \right)}^5}}\)
C. \({\frac{{1 + i}}{{1 - i}} + \frac{{1 - i}}{{1 + i}}}\)
D. \({\frac{{3 + 2i}}{{2 - i}} + \frac{{3 - 2i}}{{2 + i}}}\)
-
Bài tập 4.48 trang 209 SBT Toán 12
Cho \({z_1},{z_2} \in C\) là hai nghiệm của một phương trình bậc hai với hệ số thực. Khẳng định nào sau đây là sai?
A. \({z_1} + {z_2} \in R\)
B. \({z_1}.{z_2} \in R\)
C. \({z_1} - {z_2} \in R\)
D. \(z_1^2 + z_2^2 \in R\)
-
Bài tập 4.49 trang 209 SBT Toán 12
Cho \(k,n \in N\), biết \({\left( {1 + i} \right)^n} \in R\). Kết luận nào sau đây là đúng?
A. n = 4k+1 B. n = 4k+2
C. n = 4k+3 D. n = 4k
-
Bài tập 37 trang 208 SGK Toán 12 NC
Tìm phần thực, phần ảo của
\(\begin{array}{l}
a){\left( {2 - 3i} \right)^3} \\
b)\frac{{3 + 2i}}{{1 - i}} + \frac{{1 - i}}{{3 - 2i}} \\
c)(x + iy)^2 - 2(x + iy) + 5(x,y \in R)
\end{array}\)Với x, y nào thì số phức đó là số thực?
-
Bài tập 38 trang 209 SGK Toán 12 NC
Chứng minh rằng |z| = |w| = 1 thì số \(\frac{{z + w}}{{1 + zw}}\) là số thực (giả sử 1 + zw ≠ 0)
-
Bài tập 39 trang 209 SGK Toán 12 NC
Giải các phương trình sau trên C:
a.
\(\eqalign{{\left( {z + 3 - i} \right)^2} - 6\left( {z + 3 - i} \right) + 13 = 0}\)
b.
\(\eqalign{\left( {{{iz + 3} \over {z - 2i}}} \right)^2 - 3{{iz + 3} \over {z - 2i}} - 4 = 0;} \)
c.
\({\left( {{z^2} + 1} \right)^2} + {\left( {z + 3} \right)^2} = 0.\)
-
Bài tập 40 trang 209 SGK Toán 12 NC
Xét các số phức: \({z_1} = \sqrt 6 - i\sqrt 2 ;\) \({z_2} = - 2 - 2i;\) \({z_3} = {{{z_1}} \over {{z_2}}}\)
a. Viết \({z_1};\,{z_2};\,{z_3}\) dưới dạng lượng giác;
b. Từ câu a) hãy tính \(\cos {{7\pi } \over {12}}\) và \(\sin {{7\pi } \over {12}}\).
-
Bài tập 41 trang 209 SGK Toán 12 NC
Cho \(z = (\sqrt 6 + \sqrt 2 ) + i(\sqrt 6 - \sqrt 2 )\)
a) Viết z2 dưới dạng đại số và dưới dạng lượng giác
b) Từ câu a, hãy suy ra dạng lượng giác của z
-
Bài tập 42 trang 209 SGK Toán 12 NC
a.
Bằng cách biểu diễn hình học các số phức 2 + i và 3 + i, hãy chứng minh rằng nếu \(\tan a = {1 \over 2},\,\tan b = {1 \over 3}\)với \(a,b \in \left( {0;{\pi \over 2}} \right)\) thì \(a + b = {\pi \over 4}\).
b.
Bằng cách biển diễn hình học các số phức 2 + i, 5+ i và 8 + i, hãy chứng minh rằng nếu \(\tan a = {1 \over 2},\,\tan b = {1 \over 5},\,\tan c = {1 \over 8}\) với \(a,b,c \in \left( {0;{\pi \over 2}} \right)\) thì \(a + b + c = {\pi \over 4}\).
-
Bài tập 43 trang 210 SGK Toán 12 NC
Phần thực của \(z = 2i\) là
(A) 2; (B) 2i;
(C) 0; (D) 1.
-
Bài tập 44 trang 210 SGK Toán 12 NC
Phần ảo \(z = - 2i\) của là:
(A) - 2
(B) - 2i
(C) 0
(D) - 1
-
Bài tập 45 trang 210 SGK Toán 12 NC
Số \(z + \bar z\) là
(A) Số thực
(B) Số ảo
(C) 0
(D) 2
-
Bài tập 46 trang 210 SGK Toán 12 NC
Số \(z - \bar z\) là
(A) Số thực
(B) Số ảo
(C) 0
(D) 2i
-
Bài tập 47 trang 210 SGK Toán 12 NC
Số \(\frac{1}{{1 + i}}\) bằng
(A) \(1+i\)
(B) \(\frac{1}{2}\left( {1 - i} \right)\)
(C) \(1–i\)
(D) \(i\)
-
Bài tập 48 trang 210 SGK Toán 12 NC
Tập hợp các nghiệm của phương trình \(z = \frac{z}{{z + i}}\) là:
(A) {0;1−i}
(B) {0}
(C) {1−i}
(D) {0;1}
-
Bài tập 49 trang 210 SGK Toán 12 NC
Mođun của \(1-2i\) bằng
(A) 3
(B) \(\sqrt 5 \)
(C) 2
(D) 1
-
Bài tập 50 trang 210 SGK Toán 12 NC
Mođun của \( - 2iz\) bằng
(A) \( - 2\left| z \right|\)
(B) \(\sqrt 2 z\)
(C) \(2\left| z \right|\)
(D) 2
-
Bài tập 51 trang 210 SGK Toán 12 NC
Acgumen của \( - 1 + i\) bằng
(A) \(\frac{{3\pi }}{4} + k2\pi \left( {k \in Z} \right)\)
(B) \( - \frac{\pi }{4} + k2\pi \left( {k \in Z} \right)\)
(C) \(\frac{\pi }{4} + k2\pi \left( {k \in Z} \right)\)
(D) \(\frac{\pi }{2} + k2\pi \left( {k \in Z} \right)\)
-
Bài tập 52 trang 210 SGK Toán 12 NC
Nếu acgumen của z bằng \( - \frac{\pi }{2} + k2\pi \) thì
(A) Phần ảo của z là số dương và phần thực của z bằng 0;
(B) Phần ảo của z là số âm và phần thực của z bằng 0;
(C) Phần thực của z là số âm và phần ảo của z bằng 0;
(D) Phần thực và phần ảo của z đều là số âm.
-
Bài tập 53 trang 211 SGK Toán 12 NC
Nếu \(z = \cos \varphi - i\sin \varphi \) thì acgumen của z bằng:
(A) \(\varphi + k2\pi \left( {k \in Z} \right)\)
(B) \( - \varphi + k2\pi \left( {k \in Z} \right)\)
(C) \(\varphi + \pi + k2\pi \left( {k \in Z} \right)\)
(D) \(\varphi + \frac{\pi }{2} + k2\pi \left( {k \in Z} \right)\)
-
Bài tập 54 trang 211 SGK Toán 12 NC
Nếu \(z = - \sin \varphi - i\cos \varphi \) thì acgumen của z bằng:
(A) \( - \frac{\pi }{2} + \varphi + k2\pi \left( {k \in Z} \right)\)
(B) \( - \frac{\pi }{2} - \varphi + k2\pi \left( {k \in Z} \right)\)
(C) \(\frac{\pi }{2} + \varphi + k2\pi \left( {k \in Z} \right)\)
(D) \(\pi - \varphi + k2\pi \left( {k \in Z} \right)\)





