Bài tập 38 trang 209 SGK Toán 12 NC
Chứng minh rằng |z| = |w| = 1 thì số \(\frac{{z + w}}{{1 + zw}}\) là số thực (giả sử 1 + zw ≠ 0)
Hướng dẫn giải chi tiết
Ta có \(z.\overline z = {\left| z \right|^2} = 1 \Rightarrow \overline z = {1 \over z}\). Tương tự \(\overline {\rm{w}} = {1 \over {\rm{w}}}\)
Do đó \(\overline {\left( {{{z + {\rm{w}}} \over {1 + z{\rm{w}}}}} \right)} = {{\overline z + \overline {\rm{w}} } \over {1 + \overline z .\overline {\rm{w}} }} = {{{1 \over z} + {1 \over {\rm{w}}}} \over {1 + {1 \over z}.{1 \over {\rm{w}}}}} = {{z + {\rm{w}}} \over {1 + z{\rm{w}}}}\).
Suy ra \({{z + {\rm{w}}} \over {1 + z{\rm{w}}}}\) là số thực.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 4.49 trang 209 SBT Toán 12
Bài tập 37 trang 208 SGK Toán 12 NC
Bài tập 39 trang 209 SGK Toán 12 NC
Bài tập 40 trang 209 SGK Toán 12 NC
Bài tập 41 trang 209 SGK Toán 12 NC
Bài tập 42 trang 209 SGK Toán 12 NC
Bài tập 43 trang 210 SGK Toán 12 NC
Bài tập 44 trang 210 SGK Toán 12 NC
Bài tập 45 trang 210 SGK Toán 12 NC
Bài tập 46 trang 210 SGK Toán 12 NC
Bài tập 47 trang 210 SGK Toán 12 NC
Bài tập 48 trang 210 SGK Toán 12 NC
Bài tập 49 trang 210 SGK Toán 12 NC
Bài tập 50 trang 210 SGK Toán 12 NC
Bài tập 51 trang 210 SGK Toán 12 NC
Bài tập 52 trang 210 SGK Toán 12 NC
-


Xác định tập hợp các điểm trong mp phức biểu diễn các số phức z thỏa mãn từng điều kiện \(\left| {z - i} \right| = 1\)
bởi Lê Gia Bảo
 30/05/2020
Theo dõi (0) 1 Trả lời
30/05/2020
Theo dõi (0) 1 Trả lời -


Xác định các số phức biểu diễn bởi các đỉnh của một lục giác đều có tâm là gốc tọa độ O trong mặt phẳng phức, biết rằng một đỉnh biểu diễn số i.
bởi Nguyễn Thanh Trà
 31/05/2020
Theo dõi (0) 1 Trả lời
31/05/2020
Theo dõi (0) 1 Trả lời -


a) Biểu diễn số phức z và z' trên mp phức.
b) Biểu diễn số phức z + z' và z' – z trên mp phức.
Theo dõi (0) 1 Trả lời -


Giá trị của E bằng bao nhiêu?
bởi Ngọc Diễm
 30/05/2020
30/05/2020
Trắc nghiệm câu 1
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -
ADMICRO


Tính \(M = 1 + \left( {1 + i} \right) + {\left( {1 + i} \right)^2} + {\left( {1 + i} \right)^3} + ... + {\left( {1 + i} \right)^{20}}\)?
bởi Mai Thị Thanh Đào
 19/05/2020
19/05/2020
Giải giúp e 2 cầu này vs ạ
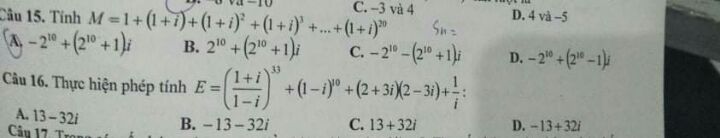 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tập hợp điểm biểu diễn số phức z thoả mãn |z-i|=| i-z | là đường thẳng đenta có phương trình
bởi Phương Thu
 14/05/2020
Tập hợp điểm biểu diễn số phức z thoả mãn |z-i|=| i-z | là đường thẳng đenta có phương trình ?Theo dõi (0) 0 Trả lời
14/05/2020
Tập hợp điểm biểu diễn số phức z thoả mãn |z-i|=| i-z | là đường thẳng đenta có phương trình ?Theo dõi (0) 0 Trả lời -


Tìm mệnh đề đúng trong các mệnh đề sau?
bởi Kim Đoan
 29/04/2020
Giải giúp em với ạ
29/04/2020
Giải giúp em với ạ Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời


