Giải bài 7 tr 45 sách GK Toán GT lớp 12
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y = x3 + 3x2 + 1
b) Dựa vào đồ thị (C), biện luận số nghiệm của phương trình sau theo m: \(x^3+3x^2+1=\frac{m}{2}\).
c) Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C).
Hướng dẫn giải chi tiết bài 7
Câu a:
y = x3 + 3x2 + 1
1) Tập xác định: D = R
2) Sự biến thiên:
Chiều biến thiên:
\(y' = 3{x^2} + 6x,y' = 0 \Leftrightarrow 3{x^2} + 6x = 0\)
\(\Leftrightarrow \bigg \lbrack \begin{matrix} x=-2\\ x=0 \end{matrix}\)
Xét dấu y':
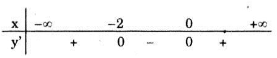
Vậy hàm số đồng biến trên các khoảng \((-\infty ;-2)\) và \((0;+\infty )\), nghịch biến trên khoảng (-2;0).
Cực trị: Hàm số đạt cực đại tại x = 0, giá trị cực đại yCĐ = y(0) = 1; đạt cực tiểu tại x = -2, giá trị cực tiểu yCT = y(-2) = 5.
Giới hạn:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } y\\
= \mathop {\lim }\limits_{x \to - \infty } ({x^3} + 3{x^2} + 1) = - \infty \\
\mathop {\lim }\limits_{x \to + \infty } y\\
= \mathop {\lim }\limits_{x \to + \infty } ({x^3} + 3{x^2} + 1) = + \infty
\end{array}\)
Bảng biến thiên:
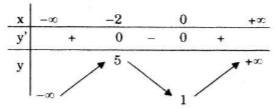
3) Đồ thị:
Ta có: y'' = 6x+6, y'' = 0 ⇔ x = - 1. Vậy đồ thị hàm số nhận điểm (-1;3) làm tâm đối xứng.
Đồ thị cắt Oy tại điểm (0;1).
Với x = -3 ⇒ y = 1
Với x = 1 ⇒ y = 5.
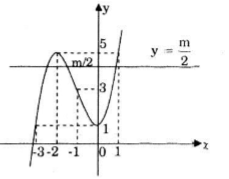
Câu b:
Số nghiệm của phương trình \(x^3+3x^2+1=\frac{m}{2} (*)\) là số giao điểm của đồ thị (C) và đường thẳng \(y=\frac{m}{2}\).
Dựa vào đồ thị trên ta có:
+ Nếu \(\left[ \begin{array}{l}
\frac{m}{2} > 5\\
\frac{m}{2} < 1
\end{array} \right. \Leftrightarrow [\begin{array}{*{20}{c}}
{m > 10}\\
{m < 2}
\end{array}\) thì (*) có một nghiệm duy nhất.
+ Nếu \(\left[ \begin{array}{l}
\frac{m}{2} = 5\\
\frac{m}{2} = 1
\end{array} \right. \Leftrightarrow [\begin{array}{*{20}{c}}
{m = 10}\\
{m = 2}
\end{array}\) thì (*) có hai nghiệm phân biệt.
+ Nếu \(1< \frac{m}{2}< 5\Leftrightarrow 2< m< 10\) thì (*) có ba nghiệm phân biệt.
Câu c:
Trong mặt phẳng, phương trình đường thẳng đi qua hai điểm A và B có tọa độ cho trước là:
\(\frac{{y - {y_B}}}{{{y_A} - {y_B}}} = \frac{{x - {x_B}}}{{{x_A} - {x_B}}}.\)
Từ câu a ta có điểm cực đại của đồ thị là (-2;5), điểm cực tiểu là (0;1). Vậy phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là:
\(\begin{array}{l}
\frac{{x + 2}}{2} = \frac{{y - 5}}{{1 - 5}}\\
\Leftrightarrow - 2x + 1 = y\\
\Leftrightarrow y = - 2x + 1
\end{array}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 5 trang 45 SGK Giải tích 12
Bài tập 6 trang 45 SGK Giải tích 12
Bài tập 8 trang 46 SGK Giải tích 12
Bài tập 9 trang 46 SGK Giải tích 12
Bài tập 10 trang 46 SGK Giải tích 12
Bài tập 11 trang 46 SGK Giải tích 12
Bài tập 12 trang 47 SGK Giải tích 12
Bài tập 1 trang 47 SGK Giải tích 12
Bài tập 2 trang 47 SGK Giải tích 12
Bài tập 3 trang 47 SGK Giải tích 12
Bài tập 4 trang 47 SGK Giải tích 12
Bài tập 5 trang 47 SGK Giải tích 12
Bài tập 1.75 trang 39 SBT Toán 12
Bài tập 1.76 trang 40 SBT Toán 12
Bài tập 1.77 trang 40 SBT Toán 12
Bài tập 1.78 trang 40 SBT Toán 12
Bài tập 1.79 trang 40 SBT Toán 12
Bài tập 1.80 trang 40 SBT Toán 12
Bài tập 1.81 trang 41 SBT Toán 12
Bài tập 1.82 trang 41 SBT Toán 12
Bài tập 1.83 trang 41 SBT Toán 12
Bài tập 1.84 trang 41 SBT Toán 12
Bài tập 1.85 trang 41 SBT Toán 12
Bài tập 1.86 trang 41 SBT Toán 12
Bài tập 1.87 trang 41 SBT Toán 12
Bài tập 1.88 trang 42 SBT Toán 12
Bài tập 1.89 trang 42 SBT Toán 12
Bài tập 1.90 trang 42 SBT Toán 12
Bài tập 1.91 trang 42 SBT Toán 12
Bài tập 1.92 trang 42 SBT Toán 12
Bài tập 1.93 trang 42 SBT Toán 12
Bài tập 1.94 trang 42 SBT Toán 12
Bài tập 1.95 trang 43 SBT Toán 12
Bài tập 1.96 trang 43 SBT Toán 12
Bài tập 68 trang 61 SGK Toán 12 NC
Bài tập 69 trang 61 SGK Toán 12 NC
Bài tập 70 trang 61 SGK Toán 12 NC
Bài tập 71 trang 62 SGK Toán 12 NC
Bài tập 72 trang 62 SGK Toán 12 NC
Bài tập 73 trang 62 SGK Toán 12 NC
Bài tập 74 trang 62 SGK Toán 12 NC
Bài tập 75 trang 62 SGK Toán 12 NC
Bài tập 76 trang 62 SGK Toán 12 NC
Bài tập 77 trang 62 SGK Toán 12 NC
Bài tập 78 trang 62 SGK Toán 12 NC
Bài tập 79 trang 62 SGK Toán 12 NC
Bài tập 80 trang 64 SGK Toán 12 NC
Bài tập 81 trang 64 SGK Toán 12 NC
Bài tập 82 trang 64 SGK Toán 12 NC
Bài tập 83 trang 64 SGK Toán 12 NC
Bài tập 84 trang 65 SGK Toán 12 NC
Bài tập 85 trang 65 SGK Toán 12 NC
Bài tập 86 trang 65 SGK Toán 12 NC
Bài tập 87 trang 65 SGK Toán 12 NC
Bài tập 88 trang 65 SGK Toán 12 NC
Bài tập 89 trang 65 SGK Toán 12 NC
Bài tập 90 trang 65 SGK Toán 12 NC
Bài tập 91 trang 65 SGK Toán 12 NC
Bài tập 92 trang 66 SGK Toán 12 NC
Bài tập 93 trang 66 SGK Toán 12 NC
Bài tập 94 trang 66 SGK Toán 12 NC
Bài tập 95 trang 66 SGK Toán 12 NC
Bài tập 96 trang 66 SGK Toán 12 NC
Bài tập 97 trang 67 SGK Toán 12 NC
Bài tập 98 trang 67 SGK Toán 12 NC
-


Với giá trị nào của m, phương trình sau \(4{x^3} - 3x - 2m + 3 = 0\) Có một nghiệm duy nhất ?
bởi Hoang Vu
 03/06/2021
03/06/2021
Với giá trị nào của m, phương trình sau \(4{x^3} - 3x - 2m + 3 = 0\) Có một nghiệm duy nhất ?
Theo dõi (0) 1 Trả lời -


Cho đồ thị (C) của hàm số \(y = {x^3} + 3{x^2} - 3x - 2\) và parabol \(y = {x^2} - 4x + 2\). Xét vị trí tương đối của đường cong (C) và parabol (tức là xác định mỗi khoảng trên đó (C) nằm phía trên hoặc phía dưới parabol).
bởi Lê Chí Thiện
 03/06/2021
03/06/2021
Cho đồ thị (C) của hàm số \(y = {x^3} + 3{x^2} - 3x - 2\) và parabol \(y = {x^2} - 4x + 2\). Xét vị trí tương đối của đường cong (C) và parabol (tức là xác định mỗi khoảng trên đó (C) nằm phía trên hoặc phía dưới parabol).
Theo dõi (0) 1 Trả lời -


Hãy tìm giao điểm của đồ thị (C) của hàm số \(y = {x^3} + 3{x^2} - 3x - 2\) và parabol \(y = {x^2} - 4x + 2\).
bởi Phạm Hoàng Thị Trà Giang
 03/06/2021
03/06/2021
Hãy tìm giao điểm của đồ thị (C) của hàm số \(y = {x^3} + 3{x^2} - 3x - 2\) và parabol \(y = {x^2} - 4x + 2\).
Theo dõi (0) 1 Trả lời -


Cho hàm số sau \(y = {x^3} - 2m(x + 1) + 1\). Với các giá trị nào của m, đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt.
bởi Nguyễn Thị Thanh
 02/06/2021
02/06/2021
Cho hàm số sau \(y = {x^3} - 2m(x + 1) + 1\). Với các giá trị nào của m, đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt.
Theo dõi (0) 1 Trả lời -
ADMICRO


Xác định giá trị của \(m\) để phương trình \(\dfrac{1}{3}{x^3} - \dfrac{1}{2}m{x^2} - 5 = 0\) có nghiệm duy nhất.
bởi na na
 02/06/2021
02/06/2021
A. \(m < \sqrt[3]{{ - 30}}\)
B. \(0 < m < 1\)
C. \(m < 0\)
D. \(m > \sqrt[3]{{ - 30}}\)
Theo dõi (0) 1 Trả lời -


Hãy xác định giá trị của tham số \(m\) để phương trình sau \({x^3} + m{x^2} + x - 5 = 0\) có nghiệm dương.
bởi Lê Nhi
 03/06/2021
03/06/2021
A. \(m = 5\)
B. \(m \in \mathbb{R}\)
C. \(m = - 3\)
D. \(m < 0\)
Theo dõi (0) 1 Trả lời -


A. Hàm số \(y = {x^3} - 5\) có hai cực trị.
B. Hàm số \(y = \dfrac{{{x^4}}}{4} + 3{x^2} - 5\) luôn đồng biến.
C. Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{3x - 2}}{{5 - x}}\) là \(y = - 3\).
D. Đồ thị hàm số \(y = \dfrac{{3{x^2} - 2x + 5}}{{{x^2} + x + 7}}\) có hai tiệm cận đứng.
Theo dõi (0) 1 Trả lời -


Hãy xác định giá trị của tham số \(m\) để phương trình sau \(2{x^3} + 3m{x^2} - 5 = 0\) có nghiệm duy nhất.
bởi Trần Phương Khanh
 03/06/2021
03/06/2021
A. \(m = \sqrt[3]{5}\)
B. \(m < \sqrt[3]{5}\)
C. \(m > \sqrt[3]{5}\)
D. \(m \in \mathbb{R}\)
Theo dõi (0) 1 Trả lời





