Bài tập 76 trang 62 SGK Toán 12 NC

a) TXĐ: D = R

\(\begin{array}{l}
y\prime  = 4{x^3} - 2x\\
y\prime  = 0 \Leftrightarrow \left\{ \begin{array}{l}
x = 0\\
x = \frac{{\sqrt 2 }}{2}\\
x =  - \frac{{\sqrt 2 }}{2}
\end{array} \right.
\end{array}\)

Hàm số đồng biến trên khoảng: 

\(\left( { - \frac{{\sqrt 2 }}{2};0} \right),\left( {\frac{{\sqrt 2 }}{2}; + \infty } \right)\)

Hàm số nghịch biến trên khoảng: 

\(\left( { - \infty ; - \frac{{\sqrt 2 }}{2}} \right),\left( {0;\frac{{\sqrt 2 }}{2}} \right)\)

 +) Cực trị:

Hàm số đạt cực đại tại: x = 0; y(0) = 0

Hàm số đạt cực tiểu tại: 

\({x =\pm \frac{{\sqrt 2 }}{2}}, y\left( { \pm \frac{{\sqrt 2 }}{2}} \right) =  - \frac{1}{4}\)

+) Giới hạn:

\(\mathop {\lim}\limits_{x \to  \pm \infty } y =  + \infty \)

Bảng biến thiên:

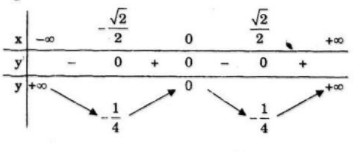
Đồ thị:

Đồ thị cắt Ox và Oy tại O(0;0) ;(−1; 0); (1; 0)

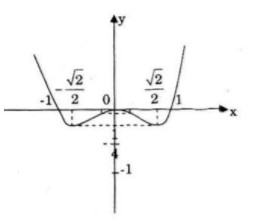
Đồ thị hàm số là hàm chẵn nên nhận trục Oy làm trục đối xứng.

b) Ta có: 

\(y = |f(x)| = \left\{ {\begin{array}{*{20}{l}}
{f(x),\,\,\,f(x) \ge 0}\\
{ - f(x),\,\,f(x) < 0}
\end{array}} \right.\)

Suy ra cách vẽ đồ thị của hàm số y = |f(x)|

Giữ nguyên phần đồ thị hàm số y = f(x) ở phía trên trục hoành. Lấy phần đồ thị hàm số ở phía dưới trục hoành đối xứng qua trục hoành. Hợp hai phần đồ thị trên ta được đồ thị hàm số y = |f(x)|

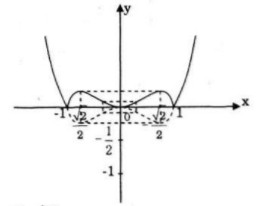
-- Mod Toán 12 HỌC247