Bài tập 77 trang 62 SGK Toán 12 NC

a) m = 1 hàm số có dạng: 

\(y = \frac{{x - 4}}{{2x - 2}}\)

Tập xác định: D = R ∖ {1}

\(y\prime  = \frac{6}{{{{(2x - 2)}^2}}} > 0,\forall x \in D\)

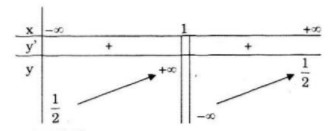
Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right);(1; + \infty )\)

Hàm số không có cực trị

Giới hạn:

\(\mathop {\lim y}\limits_{x \to {1^ - }}  =  + \infty ;\mathop {\lim y}\limits_{x \to {1^ + }}  =  - \infty \)

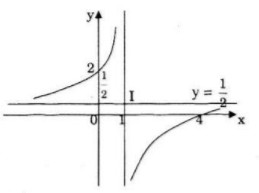
Đường tiệm cận đứng: x = 1

\(\mathop {\lim}\limits_{x \to  \pm \infty } y = \frac{1}{2}\)

Đường tiệm cận ngang y = 1/2

Bảng biến thiên:

Đồ thị:

Đồ thị giao Ox, Oy tại các điểm: (4;0); (0;2)

b) Gọi M(x₀; y₀) là một điểm bất kì của mặt phẳng tọa độ. Đường cong (H_m) đi qua điểm M khi và chỉ khi m là nghiệm của phương trình \(\frac{{{x_o} - 4m}}{{2(m{x_o} - 1)}} = {y_o}\)

\(\begin{array}{l}
 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m{x_o} - 1 \ne 0}\\
{2{y_o}(m{x_o} - 1) = {x_o} - 4m}
\end{array}} \right.\\
 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m{x_o} \ne 1\,\,(1)}\\
{(2{x_o}{y_o} + 4)m - {x_o} - 2{y_o} = 0}
\end{array}} \right.
\end{array}\)

Mọi đường cong (H_m) với \(m \ne  \pm \frac{1}{2}\) đều đi qua điểm M(x₀; y₀) khi và chỉ khi hệ phương trình trên nghiệm đúng với mọi \(m \ne  \pm \frac{1}{2}\)

Phương trình (2) nghiệm đúng với mọi m khi và chỉ khi

\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{2{x_o}{y_o} + 4 = 0}\\
{{x_o} + 2{y_o} = 0}
\end{array}} \right.\\
 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_o} =  - 2}\\
{{y_o} = 1}
\end{array}} \right. \vee \left\{ {\begin{array}{*{20}{l}}
{{x_o} = 2}\\
{{y_o} =  - 1}
\end{array}} \right.
\end{array}\)

Vậy \(\left( {{x_o};{y_o}} \right) = \left( { - 2;1} \right);\left( {{x_o};{y_o}} \right) = \left( {2; - 1} \right)\)

Ta kiểm tra điều kiện (1) 

• Với x₀ = −2, ta có m ≠ −1/2

•Với x₀ = 2, ta có m ≠ 1/2

Vậy mọi đường cong (H_m) với m ≠ ±1/2 đều đi qua hai điểm cố định A(-2; 1) và B(2; - 1).

c) Ta có: \(y\prime  = \frac{{4{m^2} - 1}}{{2{{(mx - 1)}^2}}}\)

Hệ số góc tiếp tuyến với (H_m) tại A(-2; 1) và B(2;−1) là y’(-2); y'(2).

Ta có tích hai hệ số góc tiếp tuyến tại A và B là:

\(\begin{array}{l}
y'\left( { - 2} \right).y'\left( 2 \right)\\
 = \frac{{4{m^2} - 1}}{{2{{\left( { - 2m - 1} \right)}^2}}}.\frac{{4{m^2} - 1}}{{2{{\left( {2m - 1} \right)}^2}}} = \frac{1}{4}
\end{array}\)

là hằng số

-- Mod Toán 12 HỌC247