Bài tập 68 trang 61 SGK Toán 12 NC
Chứng minh các bất đẳng thức sau:
\(\begin{array}{l}
a)\tan x > x,\forall x \in \left( {0;\frac{\pi }{2}} \right)\\
b)\tan x > x + \frac{{{x^3}}}{3},\forall x \in \left( {0;\frac{\pi }{2}} \right)
\end{array}\)
Hướng dẫn giải chi tiết
a) Hàm số f(x) = tanx − x liên tục trên nửa khoảng \(\left[ {0;\frac{\pi }{2}} \right)\) và có đạo hàm \(f'\left( x \right) = \frac{1}{{{{\cos }^2}x}} - 1 > 0\forall x\left( {0;\frac{\pi }{2}} \right)\)
Do đó hàm số f đồng biến trên nửa khoảng \(\left[ {0;\frac{\pi }{2}} \right)\)
Từ đó:
\(\begin{array}{l}
f(x) > f(0),\forall x \in \left( {0;\frac{\pi }{2}} \right)\\
\Leftrightarrow \tan x - x > 0,\forall x \in \left( {0;\frac{\pi }{2}} \right)
\end{array}\)
b) Hàm số \(f\left( x \right) = \tan x - x - \frac{{{x^3}}}{3}\) liên tục trên khoảng \(\left[ {0;\frac{\pi }{2}} \right)\) và có đạo hàm
\(\begin{array}{l}
f\prime (x) = \frac{1}{{{{\cos }^2}x - 1}}\\
= {\tan ^2}x - {x^2} > 0,\forall x \in \left( {0;\frac{\pi }{2}} \right)
\end{array}\)
(suy ra từ câu a)
Do đó hàm số f đồng biến trên nửa khoảng \(\left[ {0;\frac{\pi }{2}} \right)\) và khi đó
\(\begin{array}{l}
f(x) = f(0) = 0,\forall x \in \left( {0;\frac{\pi }{2}} \right)\\
\Rightarrow \tan x > x + \frac{{{x^3}}}{3},\forall x \in \left( {0;\frac{\pi }{2}} \right)
\end{array}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 1.95 trang 43 SBT Toán 12
Bài tập 1.96 trang 43 SBT Toán 12
Bài tập 69 trang 61 SGK Toán 12 NC
Bài tập 70 trang 61 SGK Toán 12 NC
Bài tập 71 trang 62 SGK Toán 12 NC
Bài tập 72 trang 62 SGK Toán 12 NC
Bài tập 73 trang 62 SGK Toán 12 NC
Bài tập 74 trang 62 SGK Toán 12 NC
Bài tập 75 trang 62 SGK Toán 12 NC
Bài tập 76 trang 62 SGK Toán 12 NC
Bài tập 77 trang 62 SGK Toán 12 NC
Bài tập 78 trang 62 SGK Toán 12 NC
Bài tập 79 trang 62 SGK Toán 12 NC
Bài tập 80 trang 64 SGK Toán 12 NC
Bài tập 81 trang 64 SGK Toán 12 NC
Bài tập 82 trang 64 SGK Toán 12 NC
Bài tập 83 trang 64 SGK Toán 12 NC
Bài tập 84 trang 65 SGK Toán 12 NC
Bài tập 85 trang 65 SGK Toán 12 NC
Bài tập 86 trang 65 SGK Toán 12 NC
Bài tập 87 trang 65 SGK Toán 12 NC
Bài tập 88 trang 65 SGK Toán 12 NC
Bài tập 89 trang 65 SGK Toán 12 NC
Bài tập 90 trang 65 SGK Toán 12 NC
Bài tập 91 trang 65 SGK Toán 12 NC
Bài tập 92 trang 66 SGK Toán 12 NC
Bài tập 93 trang 66 SGK Toán 12 NC
Bài tập 94 trang 66 SGK Toán 12 NC
Bài tập 95 trang 66 SGK Toán 12 NC
Bài tập 96 trang 66 SGK Toán 12 NC
Bài tập 97 trang 67 SGK Toán 12 NC
Bài tập 98 trang 67 SGK Toán 12 NC
-


Số điểm cực trị của hàm g(x) là?
bởi Híp
 20/06/2020
20/06/2020
Lầm câu 52, 53 kiểu gì ạ?
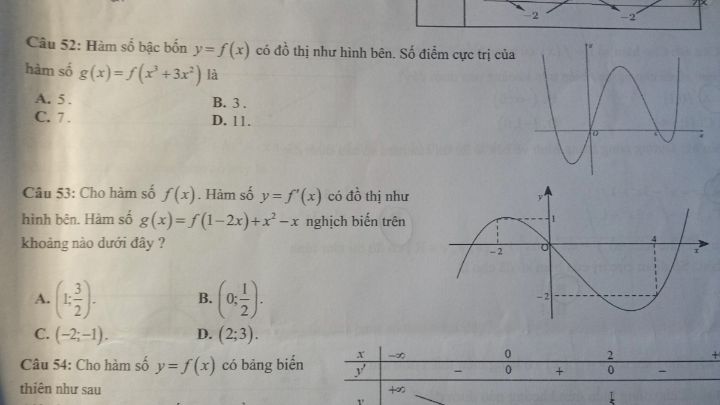 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -

Viết phương trình tiếp tuyến đạo hàm hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) biết tiếp tuyến vuông góc với đường thẳng ∆: 3x+y-2=0?
bởi Trần Lê Ánh
 18/06/2020
18/06/2020
Viết phương trình tiếp tuyến của đồ thị hàm số y= 2x-1/x+1. Biết tiếp tuyến vuông góc với đường thẳng ∆: 3x+y-2=0
Theo dõi (0) 2 Trả lời -


Có tất cả bao nhiêu giá trị thực của tham số m sao cho đồ thị của hàm số \(y = {x^3} - 2{x^2} + 4mx + x - 2m\,\,({C_1})\) và \(y = - {x^3} + 4m{x^2} - 2mx - x + 2\,\,({C_2})\)có đúng hai giao điểm phân biệt?
bởi Vân Đoàn Thị
 12/06/2020
12/06/2020
mọi người giải giúp mình câu 17, 18 với
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Số nghiệm của phương trình f^2(x)-f(x)=2 là bao nhiêu
bởi 12345
 26/04/2020
Cho hàm số y=f(x) như hình vẽ ........
26/04/2020
Cho hàm số y=f(x) như hình vẽ ........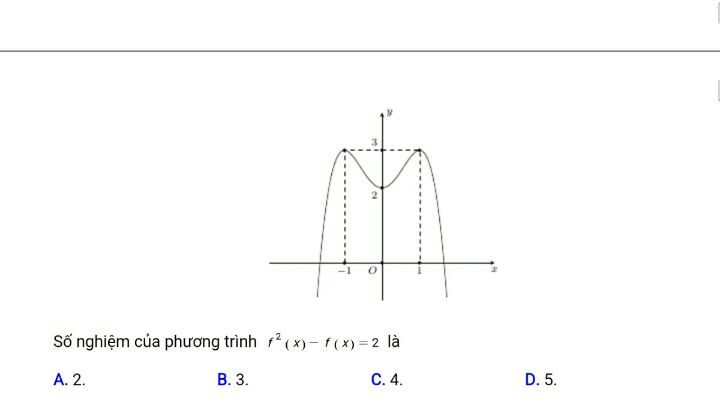 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -
ADMICRO


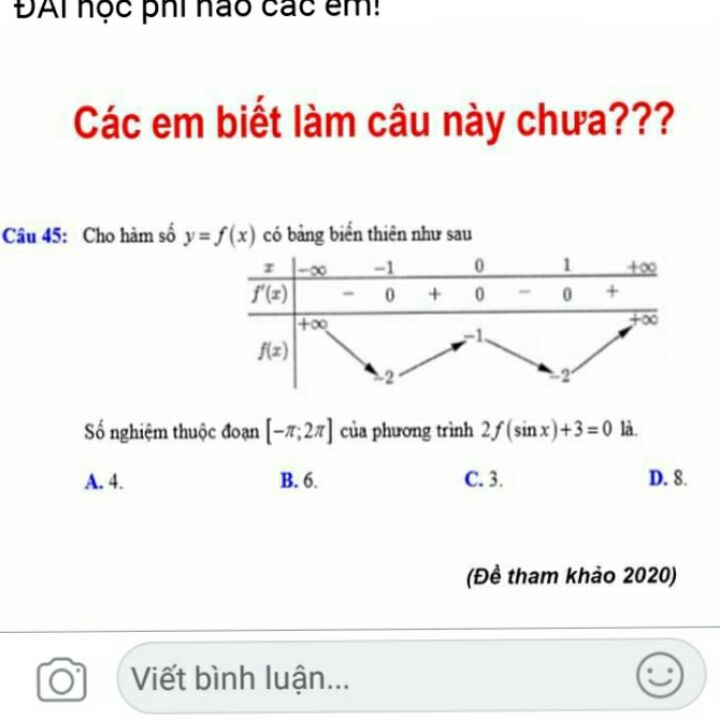
Số nghiệm thuộc đoạn \(\left[ { - \pi ;\,\,2\pi } \right]\) của phương trình \(2f(\sin x) + 3 = 0\) là?
bởi Phạm Thị.U Thương
 16/04/2020
16/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho Parabol y=(x^2-2x +3)/2 và đường thẳng d: x-y-1=0 điểm M tùy ý thuộc d sao cho tiếp tuyến từ M tới P là MT1,MT2 .T1T2 luôn đi qua điểm I cố định, tìm I.
bởi Hắss Bảo Thanh
 28/03/2020
Cho parabol y=(x^2-2x 3)/2 và đường thẳng d :x-y-1=0 điểm M tùy ý thuộc d sao cho tiếp tuyến từ M tới P là MT1,MT2 .T1T2 luôn đi qua điểm I cố định tìm ITheo dõi (0) 0 Trả lời
28/03/2020
Cho parabol y=(x^2-2x 3)/2 và đường thẳng d :x-y-1=0 điểm M tùy ý thuộc d sao cho tiếp tuyến từ M tới P là MT1,MT2 .T1T2 luôn đi qua điểm I cố định tìm ITheo dõi (0) 0 Trả lời -


Cho hàm số y=mx^3-2mx^2 + 4(m-1)-1 có đồ thị (C). Gía trị của m để đường thẳng y=-1 cắt (C) tại ba điểm phân biệt.
bởi Phong Thật Thà
 25/03/2020
25/03/2020
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Giải phương trình log2 (3x-2)=3
bởi vầy thị ơn
 03/03/2020
Hộ câu 18 với 22
03/03/2020
Hộ câu 18 với 22 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời





