Giải bài 5 tr 113 sách GK Toán GT lớp 12
Tính các tích phân sau:
a) \(\int_{0}^{1}(1+3x)^{\frac{3}{2}}dx\);
b) \(\int_{0}^{\frac{1}{2}}\frac{x^{3}-1}{x^{2}-1}dx\);
c) \(\int_{1}^{2}\dfrac{\ln(1+x)}{x^{2}}dx\).
Hướng dẫn giải chi tiết bài 5
Câu a:
Đặt u = 1 + 3x ta có: du = 3dx
Khi x = 0 thì u = 1; khi x = 1 thì u = 4.
Do đó: \(\int_{0}^{1}(1+3x)^{\frac{3}{2}}dx =\frac{1}{3}\int_{0}^{4}u^{\frac{3}{2}}du\)
\(=\frac{1}{3}\frac{2}{5}u^{\frac{5}{2}} \Bigg|_{0}^{4}= \frac{2}{15}(4^{\frac{5}{2}}-1)=\frac{62}{15}\)
Câu b:
\(\begin{array}{l}\,\,\,\int\limits_0^{\frac{1}{2}} {\dfrac{{{x^3} - 1}}{{{x^2} - 1}}dx} = \int\limits_0^{\frac{1}{2}} {\dfrac{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}dx} \\= \int\limits_0^{\frac{1}{2}} {\dfrac{{{x^2} + x + 1}}{{x + 1}}dx} = \int\limits_0^{\frac{1}{2}} {\dfrac{{x\left( {x + 1} \right) + 1}}{{x + 1}}dx} \\= \int\limits_0^{\frac{1}{2}} {\left( {x + \dfrac{1}{{x + 1}}} \right)dx} = \left. {\left( {\dfrac{{{x^2}}}{2} + \ln \left| {x + 1} \right|} \right)} \right|_0^{\frac{1}{2}}\\= \dfrac{1}{8} + \ln \dfrac{3}{2}\end{array}\)
Câu c:
\(\left\{\begin{matrix} u=ln(1+x)\\ dv=\frac{dx}{x^2} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{1}{1+x}dx\\ v=-\frac{1}{x} \end{matrix}\right.\)
Ta có:
\(\int_{1}^{2}\frac{ln(1+x)}{x^{2}}dx =-\frac{1}{x}ln(1+x) \Bigg|^2_1+ \int_{1}^{2} \frac{dx}{x(1+x)}\)
\(=-\frac{1}{2}ln 3+ln 2 +\int_{1}^{2}\frac{dx}{x(1+x)}\)
Xét \(\int_{1}^{2}\frac{dx}{(x+1)x}\). Ta có: \(\frac{1}{x(1+x)}=\frac{1}{x}-\frac{1}{x+1}\)
Do đó:
\(\int_{1}^{2}\frac{dx}{x(x+1)}=\int_{1}^{2}\left ( \frac{1}{x}- \frac{1}{x+1} \right )dx=\int_{1}^{2}\frac{dx}{x}-\int_{1}^{2}\frac{dx}{x+1}\)
\(=lnx \Bigg|^2_1-ln(1+x)\Bigg|^2_1=ln2 -ln3+ln2\)
Vậy \(\int_{1}^{2}\frac{ln(1+x)}{x^2}dx=-\frac{1}{2}ln3 +ln2 +ln2-ln3+ln2\)
\(=3ln2-\frac{3}{2}ln3=ln8-\frac{3}{2}ln3=3ln \frac{2\sqrt{3}}{3}\)
-- Mod Toán 12 HỌC247
Video hướng dẫn giải bài 5 SGK
Bài tập SGK khác
Bài tập 3 trang 113 SGK Giải tích 12
Bài tập 4 trang 113 SGK Giải tích 12
Bài tập 6 trang 113 SGK Giải tích 12
Bài tập 3.16 trang 170 SBT Toán 12
Bài tập 3.17 trang 170 SBT Toán 12
Bài tập 3.18 trang 171 SBT Toán 12
Bài tập 3.19 trang 171 SBT Toán 12
Bài tập 3.20 trang 172 SBT Toán 12
Bài tập 3.21 trang 172 SBT Toán 12
Bài tập 3.22 trang 172 SBT Toán 12
Bài tập 3.23 trang 172 SBT Toán 12
Bài tập 3.24 trang 172 SBT Toán 12
Bài tập 3.25 trang 173 SBT Toán 12
Bài tập 3.26 trang 173 SBT Toán 12
Bài tập 3.28 trang 173 SBT Toán 12
Bài tập 3.27 trang 173 SBT Toán 12
Bài tập 3.29 trang 173 SBT Toán 12
Bài tập 3.30 trang 173 SBT Toán 12
Bài tập 10 trang 152 SGK Toán 12 NC
Bài tập 11 trang 152 SGK Toán 12 NC
Bài tập 12 trang 153 SGK Toán 12 NC
Bài tập 13 trang 153 SGK Toán 12 NC
Bài tập 14 trang 153 SGK Toán 12 NC
Bài tập 15 trang 153 SGK Toán 12 NC
Bài tập 16 trang 153 SGK Toán 12 NC
Bài tập 17 trang 161 SGK Toán 12 NC
Bài tập 18 trang 161 SGK Toán 12 NC
Bài tập 19 trang 161 SGK Toán 12 NC
Bài tập 20 trang 161 SGK Toán 12 NC
Bài tập 21 trang 161 SGK Toán 12 NC
Bài tập 22 trang 162 SGK Toán 12 NC
Bài tập 23 trang 162 SGK Toán 12 NC
-
Tính tích phân sau: \(\int\limits_{ - 2}^0 {\left( {x - {e^{ - x}}} \right)dx} \)
bởi hoàng duy
25/05/2021
Tính tích phân sau: \(\int\limits_{ - 2}^0 {\left( {x - {e^{ - x}}} \right)dx} \)
Theo dõi (0) 1 Trả lời -
Tính tích phân sau: \(\int\limits_2^5 {{{\left( {3x - 4} \right)}^4}dx} \).
Theo dõi (0) 1 Trả lời -
Tính tích phân sau: \(\int\limits_0^1 {\left( {{e^{2x}} + {3 \over {x + 1}}} \right)dx} \).
bởi thu thủy
25/05/2021
Tính tích phân sau: \(\int\limits_0^1 {\left( {{e^{2x}} + {3 \over {x + 1}}} \right)dx} \).
Theo dõi (0) 1 Trả lời -
Tính tích phân sau: \(\int\limits_2^4 {{{\left( {x + {1 \over x}} \right)}^2}dx} \).
bởi Đan Nguyên
24/05/2021
Tính tích phân sau: \(\int\limits_2^4 {{{\left( {x + {1 \over x}} \right)}^2}dx} \).
Theo dõi (0) 1 Trả lời -
ADMICRO
Cho hàm số y = f(x) liên tục trên R{0;-1} thỏa mãn
bởi Linh Võ
14/05/2021
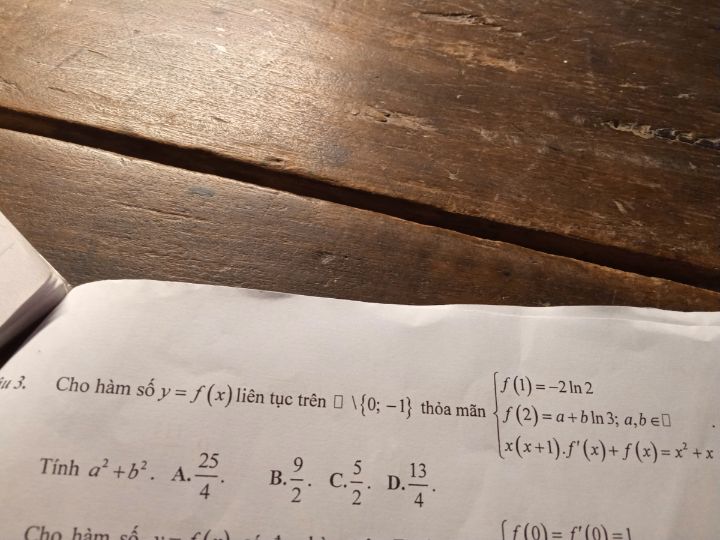Theo dõi (0) 0 Trả lời -
A. \(2\left( {\sin 1 - \cos 1} \right)\)
B. \(\sin 1 - \cos 1\)
C. \(2\left( {\cos 1 - \sin 1} \right)\)
D. \(2\left( {\sin 1 + \cos 1} \right)\)
Theo dõi (0) 1 Trả lời -
Đối với tích phân \(\int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{\tan x}}{{{{\cos }^2}x}}dx} \), thực hiện đổi biến số \(t = \tan x\) ta được:
bởi Sasu ka
09/05/2021
A. \(\int\limits_0^{\dfrac{\pi }{4}} {tdt} \)
B. \(\int\limits_{ - 1}^0 {tdt} \)
C. \(\int\limits_0^1 {tdt} \)
D. \( - \int\limits_0^1 {tdt} \)
Theo dõi (0) 1 Trả lời -
A. \( - 1 - \dfrac{1}{e}\)
B. \(1 - \dfrac{2}{e}\)
C. \( - 1 + \dfrac{2}{e}\)
D. \(0\)
Theo dõi (0) 1 Trả lời -
\(\int\limits_{ - \dfrac{\pi }{2}}^{\dfrac{\pi }{2}} {\left( {\dfrac{{\sin 2x\sin x}}{2} + {{\cos }^3}x} \right)dx} \) bằng:
bởi Tieu Giao
10/05/2021
A. \(2\)
B. \( - 1\)
C. \(\pi \)
D. \( - \pi \)
Theo dõi (0) 1 Trả lời -
A. \(\dfrac{1}{2}\)
B. \(2\)
C. \( - 1\)
D. \(0\)
Theo dõi (0) 1 Trả lời -
Hãy chỉ ra kết quả sai trong việc khử giá trị tuyệt đối của tích phân sau đây:\(\int\limits_0^{2\pi } {\left| {\sin x} \right|dx} \).
bởi bich thu
09/05/2021
A. \(\int\limits_0^{2\pi } {\sin xdx} \)
B. \(\int\limits_0^\pi {2\sin xdx} \)
C. \(\int\limits_0^\pi {\sin xdx} - \int\limits_\pi ^{2\pi } {\sin xdx} \)
D. \( - \int\limits_0^{2\pi } {2\sin xdx} \)
Theo dõi (0) 1 Trả lời -
Đặt \({I_n} = \int\limits_0^{\dfrac{\pi }{2}} {{{\sin }^n}xdx} ,n \in {N^*}\). Chứng minh rằng \({I_n} = \dfrac{{n - 1}}{n}{I_{n - 2}},n > 2\).
bởi Nguyễn Thị An
10/05/2021
Đặt \({I_n} = \int\limits_0^{\dfrac{\pi }{2}} {{{\sin }^n}xdx} ,n \in {N^*}\). Chứng minh rằng \({I_n} = \dfrac{{n - 1}}{n}{I_{n - 2}},n > 2\).
Theo dõi (0) 1 Trả lời -
Giả sử hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Chứng minh rằng: \(\int\limits_0^{\dfrac{\pi }{2}} {f(\sin x)dx} = \int\limits_0^{\dfrac{\pi }{2}} {f(\cos x)dx} \)
bởi Thuy Kim
09/05/2021
Giả sử hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Chứng minh rằng: \(\int\limits_0^{\dfrac{\pi }{2}} {f(\sin x)dx} = \int\limits_0^{\dfrac{\pi }{2}} {f(\cos x)dx} \)
Theo dõi (0) 1 Trả lời -
Giả sử hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - a;a} \right]\). Chứng minh rằng: \(\int\limits_{ - a}^a {f(x)dx = } \left\{ \begin{array}{l}2\int\limits_0^a {f(x)dx} \,\,\left( 1 \right)\\0,\,\,\,\left( 2 \right)\end{array} \right.\)
bởi Thùy Nguyễn
10/05/2021
(1): nếu \(f\) là hàm số chẵn.
(2): nếu \(f\) là hàm số lẻ.
Áp dụng để tính: \(\int\limits_{ - 2}^2 {\ln \left( {x + \sqrt {1 + {x^2}} } \right)dx} \)
Theo dõi (0) 1 Trả lời -
Chứng minh rằng hàm số \(f\left( x \right)\) cho bởi \(f(x) = \int\limits_0^x {\dfrac{t}{{\sqrt {1 + {t^4}} }}dt} ,x \in \mathbb{R}\) là hàm số chẵn.
bởi Naru to
10/05/2021
Chứng minh rằng hàm số \(f\left( x \right)\) cho bởi \(f(x) = \int\limits_0^x {\dfrac{t}{{\sqrt {1 + {t^4}} }}dt} ,x \in \mathbb{R}\) là hàm số chẵn.
Theo dõi (0) 1 Trả lời -
Tính tích phân sau đây: \(I = \int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{\sin 2xdx}}{{3 + 4\sin x - \cos 2x}}} \).
bởi Hoàng My
10/05/2021
Tính tích phân sau đây: \(I = \int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{\sin 2xdx}}{{3 + 4\sin x - \cos 2x}}} \).
Theo dõi (0) 1 Trả lời -
Tính tích phân sau đây: \(I = \int\limits_{\dfrac{1}{2}}^1 {\dfrac{{{x^2} - 1}}{{{x^4} + 1}}} dx\).
bởi Hồng Hạnh
10/05/2021
Tính tích phân sau đây: \(I = \int\limits_{\dfrac{1}{2}}^1 {\dfrac{{{x^2} - 1}}{{{x^4} + 1}}} dx\).
Theo dõi (0) 1 Trả lời
