Giải bài 3.21 tr 172 SBT Toán 12
Giả sử hàm số f(x) liên tục trên đoạn [-a;a]. Chứng minh rằng
\(\int \limits_{ - a}^a f\left( x \right)dx = \left\{ \begin{array}{l}
2\int \limits_0^a f\left( x \right)\\
0
\end{array} \right.\)
nếu \(f\) chẵn hoặc \(f\) lẻ.
Áp dụng để tính \(\int \limits_{ - 2}^2 \ln \left( {x + \sqrt {1 + {x^2}} } \right)dx\)
Hướng dẫn giải chi tiết
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [−a;a], ta có:
\(\int \limits_{ - a}^a f(x)dx = \int \limits_{ - a}^0 f(x)dx + \int \limits_0^a f(x)dx\)
Đổi biến x = −t đối với tích phân \(\int \limits_{ - a}^0 f(x)dx\), ta được:
\(\int \limits_{ - a}^0 f(x)dx = - \int \limits_a^0 f( - t)dt = \int\limits_0^a {f\left( t \right)dt = \int\limits_0^a {f\left( x \right)dx} } \)
Vậy \(\int \limits_{ - a}^a f(x)dx = 2\int \limits_0^a f(x)dx\)
Trường hợp sau chứng minh tương tự.
Áp dụng:
Ta có:
\(\begin{array}{l}
g( - x) = \ln \left( { - x + \sqrt {1 + {{\left( { - x} \right)}^2}} } \right) = \ln \left( {\frac{1}{{x + \sqrt {1 + {x^2}} }}} \right)\\
= - \ln \left( {x + \sqrt {1 + {x^2}} } \right) = - g\left( x \right)
\end{array}\)
Nên \(g(x) = \ln \left( {x + \sqrt {1 + {x^2}} } \right)\) là hàm số lẻ trên đoạn [−2;2] nên \(\int \limits_{ - 2}^2 g(x)dx = 0\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.19 trang 171 SBT Toán 12
Bài tập 3.20 trang 172 SBT Toán 12
Bài tập 3.22 trang 172 SBT Toán 12
Bài tập 3.23 trang 172 SBT Toán 12
Bài tập 3.24 trang 172 SBT Toán 12
Bài tập 3.25 trang 173 SBT Toán 12
Bài tập 3.26 trang 173 SBT Toán 12
Bài tập 3.28 trang 173 SBT Toán 12
Bài tập 3.27 trang 173 SBT Toán 12
Bài tập 3.29 trang 173 SBT Toán 12
Bài tập 3.30 trang 173 SBT Toán 12
Bài tập 10 trang 152 SGK Toán 12 NC
Bài tập 11 trang 152 SGK Toán 12 NC
Bài tập 12 trang 153 SGK Toán 12 NC
Bài tập 13 trang 153 SGK Toán 12 NC
Bài tập 14 trang 153 SGK Toán 12 NC
Bài tập 15 trang 153 SGK Toán 12 NC
Bài tập 16 trang 153 SGK Toán 12 NC
Bài tập 17 trang 161 SGK Toán 12 NC
Bài tập 18 trang 161 SGK Toán 12 NC
Bài tập 19 trang 161 SGK Toán 12 NC
Bài tập 20 trang 161 SGK Toán 12 NC
Bài tập 21 trang 161 SGK Toán 12 NC
Bài tập 22 trang 162 SGK Toán 12 NC
Bài tập 23 trang 162 SGK Toán 12 NC
-


Nếu \(\int\limits_0^2 {f(x)dx = 3} \) thì \(\int\limits_0^2 {\left[ {4f(x) - 3} \right]dx} \) bằng bao nhiêu?
bởi trịnh duy quang đạt
 04/08/2020
04/08/2020
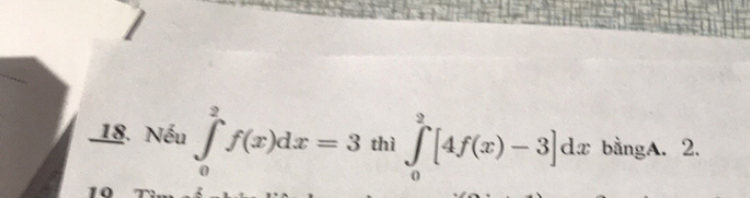 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tính \(I = \int\limits_0^3 {f(x)dx} \)?
bởi Thúy Vy
 01/08/2020
01/08/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giá trị của biểu thức A=2a-b là bao nhiêu?
bởi vũ tiến đạt
 29/07/2020
29/07/2020
Câu 33
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho hàm số f(x) có đạo hàm liên tục trên [0;2] , khi đó \(\int\limits_0^2 {f(x)dx} \) bằng bao nhiêu?
bởi nguyễn quang hoàng
 12/07/2020
12/07/2020
Mn giúp câu 48 với
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm tất cả x,y sao cho \(x^2-1 + yi= -1+ 2i\)?
bởi Trần Bá Đạt
 29/06/2020
29/06/2020
Tìm tất cả x,y sao cho x^2-1 yi=-1 2i
Theo dõi (0) 2 Trả lời -


Tính tích phân \(I = \int\limits_0^1 {{x^3}\left( {1 + x\sqrt {1 - {x^2}} } \right)dx} \)?
bởi Anh Phong
 18/06/2020
18/06/2020
Tính tích phân \(I = \int\limits_0^1 {{x^3}\left( {1 + x\sqrt {1 - {x^2}} } \right)dx} \)?
Theo dõi (1) 2 Trả lời -


Tính f(-1)?
bởi ma thị nhung
 12/06/2020
12/06/2020
Xin đáp án và giải chi tiết ạ
Câu 28
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính tích phân
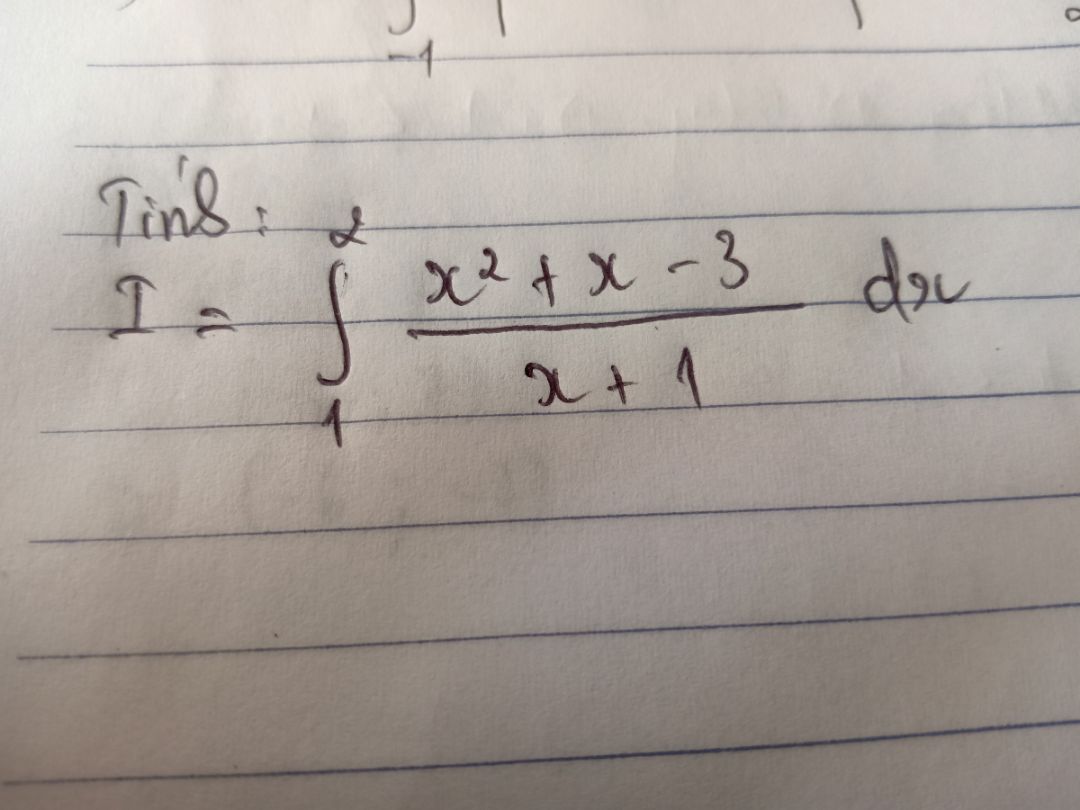 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính tích phân
 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Tính tích phân \(\frac{1}{{\sqrt x }}\)?
bởi Nguyen Tuyet
 11/06/2020
11/06/2020
Nhờ mn Giải ra từng bước hộ
Tính tích phân \(\frac{1}{{\sqrt x }}\)?
Theo dõi (0) 6 Trả lời -


Nếu (intlimits_1^3 {f(x)dx = 3} ) thì (intlimits_1^5 {fleft( {frac{{x + 1}}{2}} ight)dx} ) bằng?
bởi Diệu Cutee
 10/06/2020
10/06/2020
Giải giùm câu 35
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính \(\int\limits_1^2 {f(x)dx} \)? Biết \(f(2x)=3f(x)\) và \(\int\limits_0^1 {f(x)dx} = 1\)
bởi Kim Oanh
 08/06/2020
08/06/2020
Cho hàm số f(x) thỏa mãn \(f(2x)=3f(x)\)với mọi x thuộc R . Biết \(\int\limits_0^1 {f(x)dx} = 1\). Tính \(\int\limits_1^2 {f(x)dx}\)
Theo dõi (0) 1 Trả lời -


\(I = \int\limits_0^1 {\frac{{2\cos x}}{{\sin + \cos x}}dx = \frac{{a\pi }}{2} + b} \) thì a + b bằng?
bởi Tường Vy
 04/06/2020
04/06/2020
Mọi người giúp e giải câu này với ạ. E cảm ơn❤
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


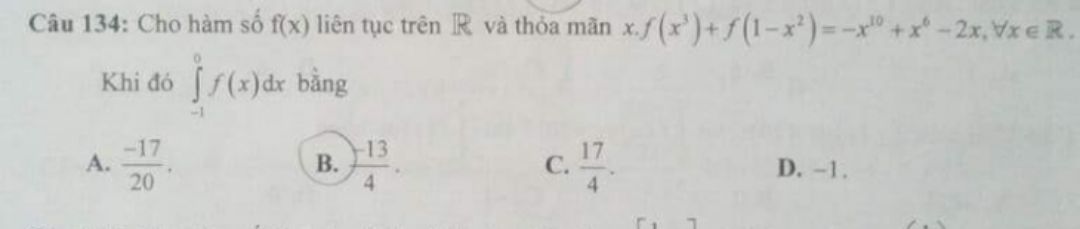 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


\(\int\limits_0^{\frac{\pi }{2}} {\frac{{\cos x}}{{{{\sin }^2}x - 5\sin x + 6}} = a\ln \frac{a}{b}} \) Giá trị của \(a+b\) là?
bởi Anh Tuan
 30/05/2020
30/05/2020
Giải chi tiết giúp mình với.
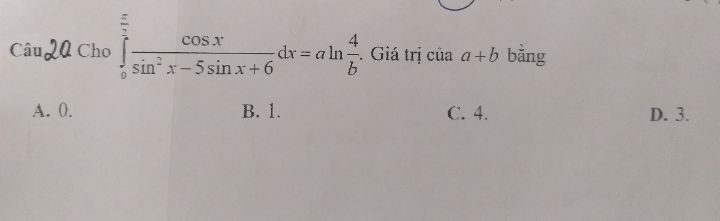 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


\(\int\limits_1^{\ln 3} {xf(x)dx} \) bằng bao nhiêu?
bởi Kiều Trang
 29/05/2020
29/05/2020
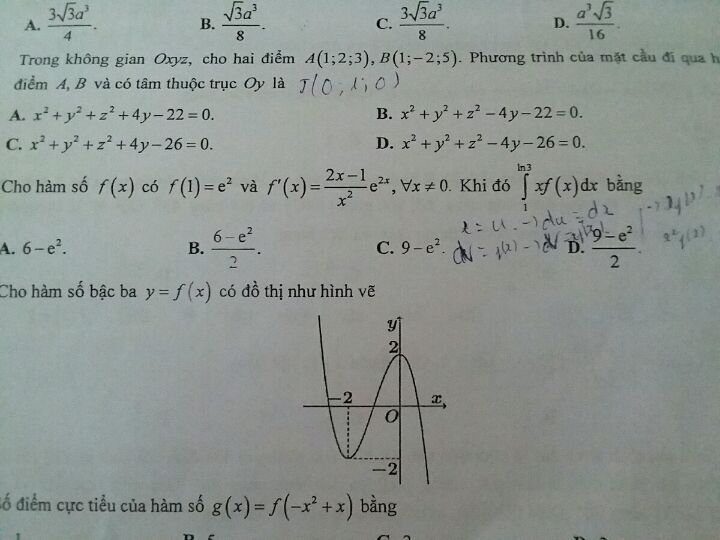 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời



