Giải bài 3.20 tr 172 SBT Toán 12
Chứng minh rằng hàm số cho bởi \(\int \limits_0^x \frac{t}{{\sqrt {1 + {t^4}} }}dt,x \in R\) là hàm số chẵn.
Hướng dẫn giải chi tiết
Ta có: \(f( - x) = \int \limits_0^{ - x} \frac{t}{{\sqrt {1 + {t^4}} }}dt,x \in R\)
Đặt , khi đó: \(f( - x) = \int \limits_0^x \frac{s}{{\sqrt {1 + {s^4}} }}ds = f(x)\)
Vậy \(f(x)\) là hàm số chẵn.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.18 trang 171 SBT Toán 12
Bài tập 3.19 trang 171 SBT Toán 12
Bài tập 3.21 trang 172 SBT Toán 12
Bài tập 3.22 trang 172 SBT Toán 12
Bài tập 3.23 trang 172 SBT Toán 12
Bài tập 3.24 trang 172 SBT Toán 12
Bài tập 3.25 trang 173 SBT Toán 12
Bài tập 3.26 trang 173 SBT Toán 12
Bài tập 3.28 trang 173 SBT Toán 12
Bài tập 3.27 trang 173 SBT Toán 12
Bài tập 3.29 trang 173 SBT Toán 12
Bài tập 3.30 trang 173 SBT Toán 12
Bài tập 10 trang 152 SGK Toán 12 NC
Bài tập 11 trang 152 SGK Toán 12 NC
Bài tập 12 trang 153 SGK Toán 12 NC
Bài tập 13 trang 153 SGK Toán 12 NC
Bài tập 14 trang 153 SGK Toán 12 NC
Bài tập 15 trang 153 SGK Toán 12 NC
Bài tập 16 trang 153 SGK Toán 12 NC
Bài tập 17 trang 161 SGK Toán 12 NC
Bài tập 18 trang 161 SGK Toán 12 NC
Bài tập 19 trang 161 SGK Toán 12 NC
Bài tập 20 trang 161 SGK Toán 12 NC
Bài tập 21 trang 161 SGK Toán 12 NC
Bài tập 22 trang 162 SGK Toán 12 NC
Bài tập 23 trang 162 SGK Toán 12 NC
-


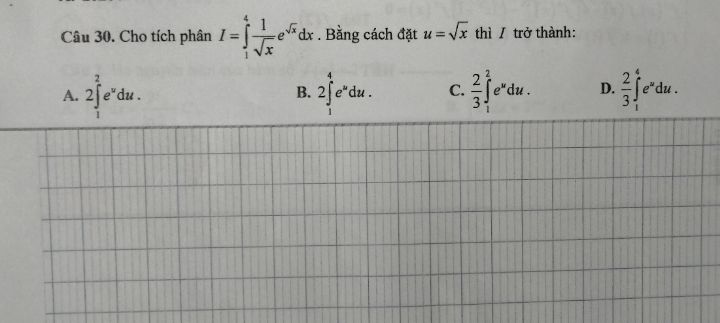 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Cho 1 ∫ 0 (x+1)exdx=a+b.e. Tính i=ab
bởi Kuu Lầyy
 27/03/2021
27/03/2021
ai giải giùm e ạ
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Cho tích phân π2∫0f(x)dx=5∫0π2f(x)dx=5. Tính tích phân I=π2∫0[f(x)+2sinx]dxI=∫0π2[f(x)+2sinx]dx.
Theo dõi (0) 3 Trả lời -
ADMICRO


Biết tích phân với a, b là các số nguyên khác 0. Tính ab
bởi Hờ Dem
 18/03/2021
Giải câu 9 10 hộ mình
18/03/2021
Giải câu 9 10 hộ mình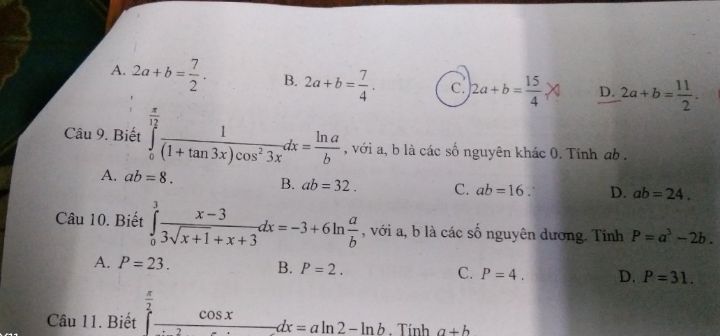 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính tích phân
bởi Nguyễn Minh Thư
 07/03/2021
07/03/2021
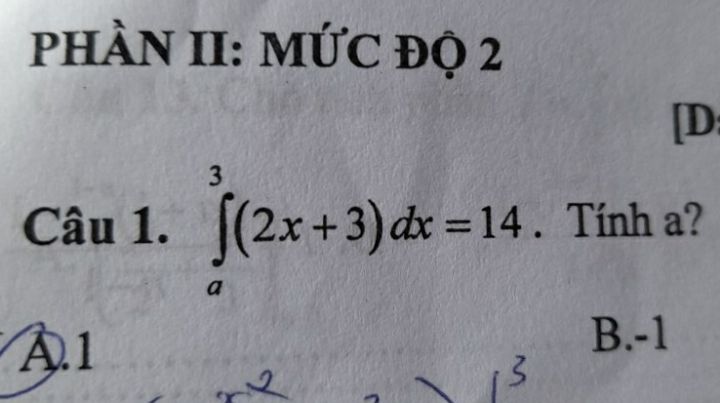 Theo dõi (1) 14 Trả lời
Theo dõi (1) 14 Trả lời -


Tích phân từ 1 đến e của (1 - x^2).lnxdx
bởi Lợt Nguyễn
 27/02/2021
27/02/2021
Tích phân từ 1 đến e của (1 - x^2).lnxdx
Theo dõi (0) 1 Trả lời -


Tính tích phân sau:
bởi Cúc Nguyễn Thanh
 24/02/2021
24/02/2021
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính tích phân
bởi Cúc Nguyễn Thanh
 24/02/2021
24/02/2021
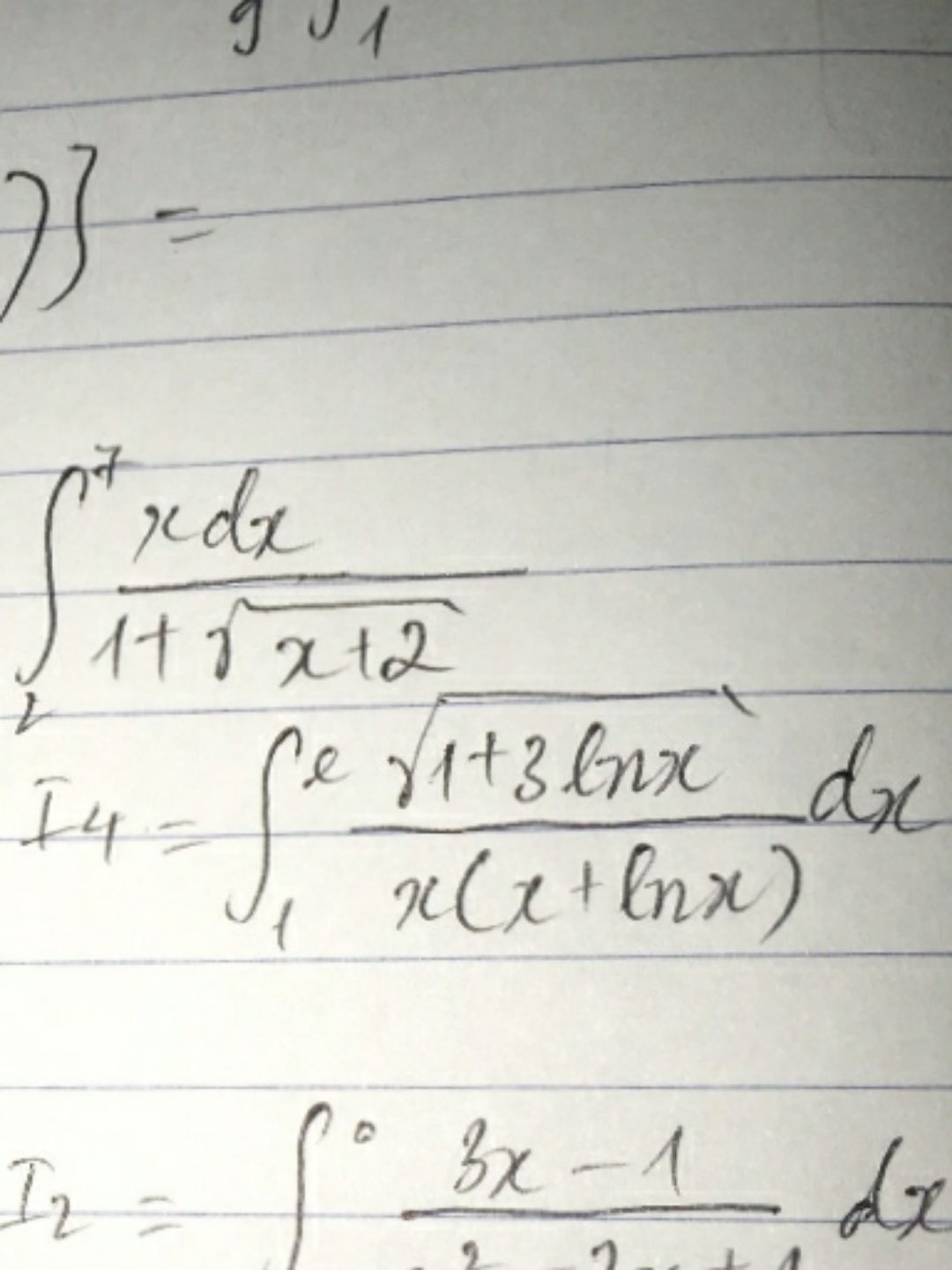 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho f(x) = ax^2 + b có đạo hàm trên (0;a), f(0) = 3a
bởi Kim's Xuân's
 23/02/2021
23/02/2021
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính tích phân từ 0 đến 1 của 3/(x^3 +1).
bởi Nguyễn Tuấn Minh
 21/02/2021
21/02/2021
tính tích phân từ 0 đến 1 của 3/(x^3 +1)
Theo dõi (0) 0 Trả lời -


Tính tích phân Ln2|2x.e^(x^2)dx1
bởi Baang Baang
 18/02/2021
Ln2|2x.e^(x^2)dx1Tính tích phân ạTheo dõi (0) 0 Trả lời
18/02/2021
Ln2|2x.e^(x^2)dx1Tính tích phân ạTheo dõi (0) 0 Trả lời -


Tính tích phân từ 0 đến a (x^3 x) / căn (x^2 1) dx
bởi Nhậtt Vy
 18/02/2021
Tính tích phân từ 0 đến a (x^3 x) / căn (x^2 1) dxTheo dõi (0) 0 Trả lời
18/02/2021
Tính tích phân từ 0 đến a (x^3 x) / căn (x^2 1) dxTheo dõi (0) 0 Trả lời -


Cho F(x)=x là nguên hàm của f(x)*x . Tìm nguyên hàm của hàm số f'(x)*x^2/2
bởi Huỳnh Giao
 07/02/2021
07/02/2021
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính tích phân: ∫π2π4esinxcosxdx
bởi Xuân Hoàng
 27/01/2021
Tính
27/01/2021
Tính Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tích phân từ 1 đến 4 căng x
bởi Thanh Vương
 19/01/2021
19/01/2021
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính nguyên hàm: lnx/x^3
bởi Phạm Thị Kim Loan
 19/01/2021
Nguyên hàm lnx/x^3Theo dõi (0) 0 Trả lời
19/01/2021
Nguyên hàm lnx/x^3Theo dõi (0) 0 Trả lời



