Bài tập 10 trang 152 SGK Toán 12 NC
Không tìm nguyên hàm hãy tính các tích phân sau:
\(\begin{array}{l}
a)\int\limits_{ - 2}^4 {\left( {\frac{x}{2} + 3} \right)dx} \\
b)\int \limits_{ - 1}^2 \left| x \right|dx\\
c)\int \limits_{ - 3}^3 \sqrt {9 - {x^2}} dx
\end{array}\)
Hướng dẫn giải chi tiết
a) Tích phân đó bằng diện tích hình thang ABCD với cạnh nghiêng là đường thẳng \(y = \frac{x}{2} + 3\). Diện tích đó là \((2 + 5)\frac{6}{2} = 21\).
Vậy \(\int\limits_{ - 2}^4 {\left( {\frac{x}{2} + 3} \right)dx} = 21\)
.png)
b)
.png)
Từ hình trên ta thấy hình A gồm 2 tam giác. Do đó tích phân bằng diện tích của A là \(\frac{1}{2}.1.1 + \frac{1}{2}2.2 = 0,5 + 2 = 2,5\)
Vậy \(\int \limits_{ - 1}^2 \left| x \right|dx = \frac{5}{2}\)
c) Tích phân bằng diện tích nửa đường tròn x2 + y2 = 9 (hình). Đây là đường tròn tâm là gốc tọa độ bán kính là 3. Do đó diện tích nửa dường tròn là \(9\frac{\pi }{2} = 4,5\pi .\)
Vậy \(\int \limits_{ - 3}^3 \sqrt {9 - {x^2}} dx = 4,5\pi \)
.png)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.29 trang 173 SBT Toán 12
Bài tập 3.30 trang 173 SBT Toán 12
Bài tập 11 trang 152 SGK Toán 12 NC
Bài tập 12 trang 153 SGK Toán 12 NC
Bài tập 13 trang 153 SGK Toán 12 NC
Bài tập 14 trang 153 SGK Toán 12 NC
Bài tập 15 trang 153 SGK Toán 12 NC
Bài tập 16 trang 153 SGK Toán 12 NC
Bài tập 17 trang 161 SGK Toán 12 NC
Bài tập 18 trang 161 SGK Toán 12 NC
Bài tập 19 trang 161 SGK Toán 12 NC
Bài tập 20 trang 161 SGK Toán 12 NC
Bài tập 21 trang 161 SGK Toán 12 NC
Bài tập 22 trang 162 SGK Toán 12 NC
Bài tập 23 trang 162 SGK Toán 12 NC
-


Tính tích phân từ 1 đến e của lnx/x^2dx
bởi Kim Tuyền
 26/12/2019
Tính tích phân sau:
26/12/2019
Tính tích phân sau: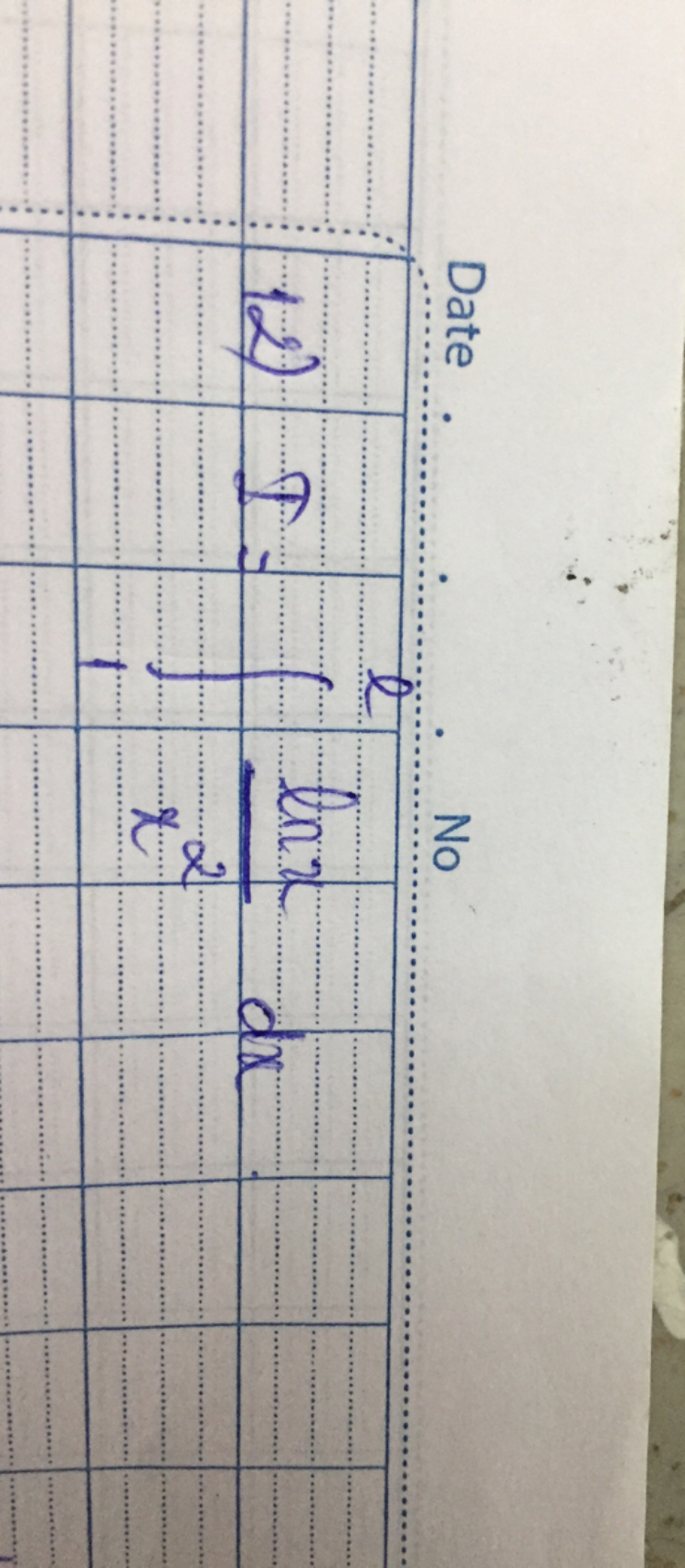 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính tích phân từ 0 đến 1 của (3x-1)^3dx
bởi Thien Vuong
 24/12/2019
24/12/2019
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm nguyên hàm của hàm số cosx/(2+sinx)^2
bởi Bùi Kim Hai
 22/12/2019
22/12/2019
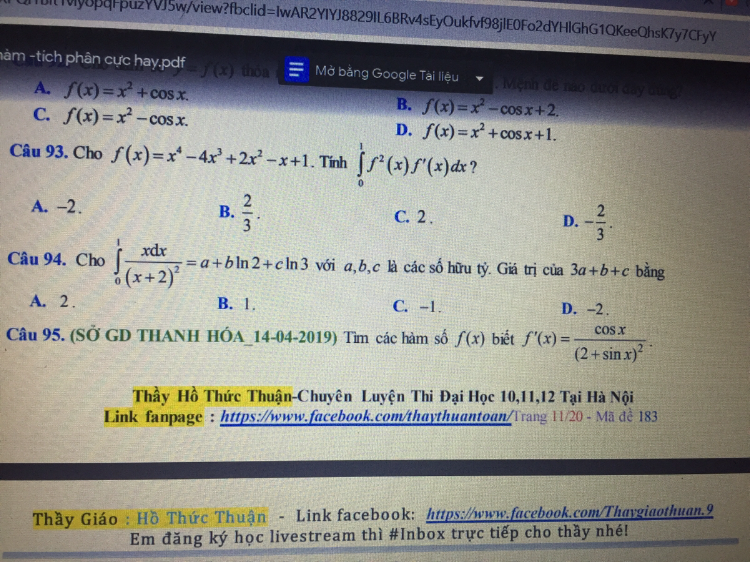 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính f(4) biết hàm số f(x) liên tục trên đoạn (2,4)
bởi lê thị yến
 11/12/2019
11/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Khi nào thì đổi cận, đặt ẩn là t có phải đổi cận không?
bởi ngọc Đào
 08/12/2019
Khi nào thì đổi cận, đặt ẩn là t có phải đổi cận khôngTheo dõi (0) 0 Trả lời
08/12/2019
Khi nào thì đổi cận, đặt ẩn là t có phải đổi cận khôngTheo dõi (0) 0 Trả lời -


Tính tích phân từ 2 đến 3 căn 15 của căn(x^3+1)/x
bởi Lê Anh Cta
 07/12/2019
Giải họi t vs ạ
07/12/2019
Giải họi t vs ạ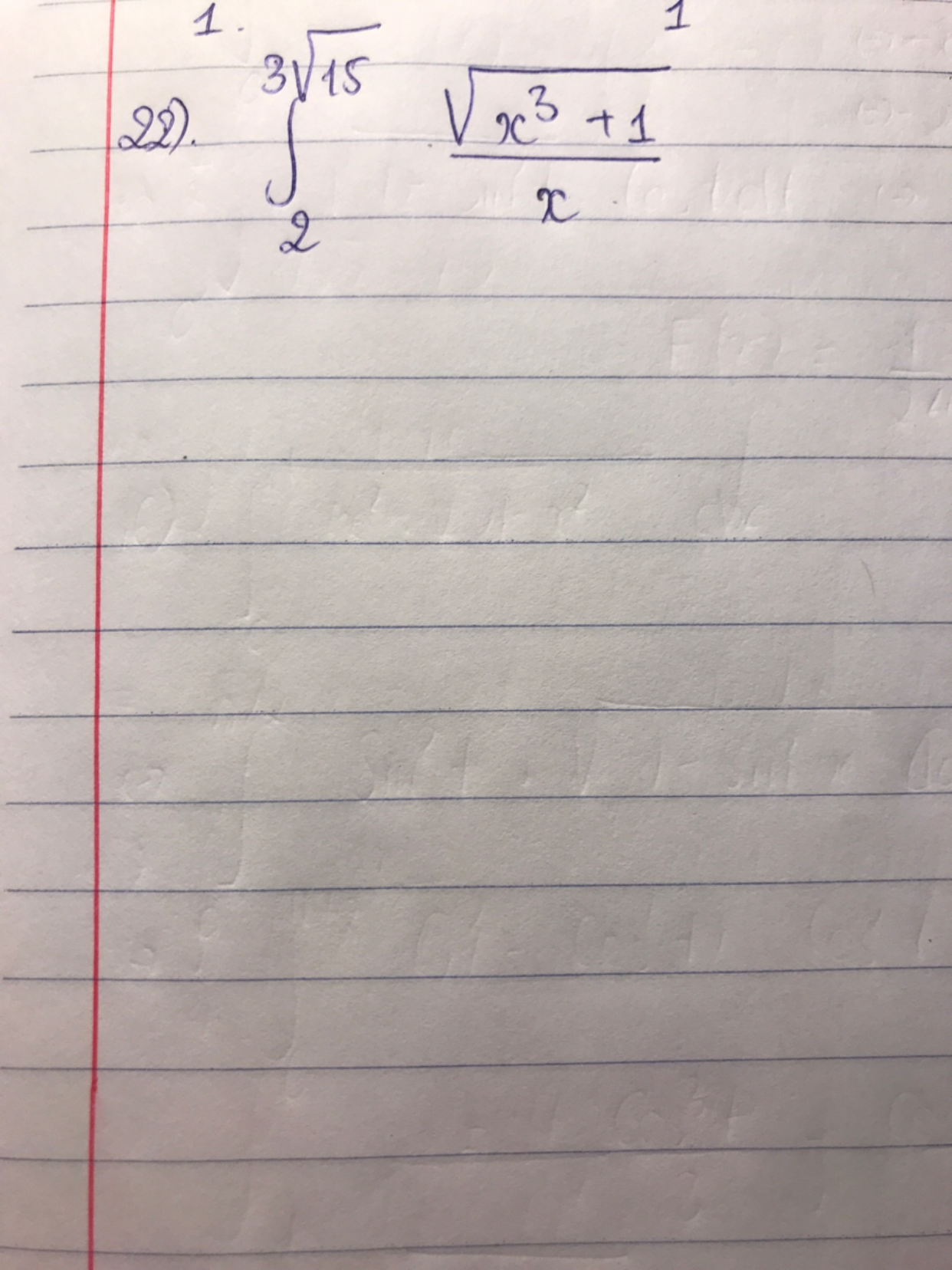 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Giải giúp e bài 2 với ạ
Giải giúp e bài 2 với ạ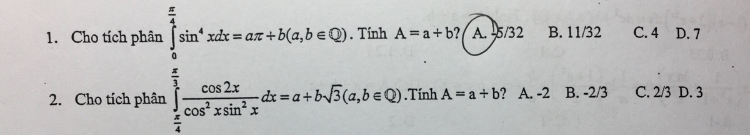 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


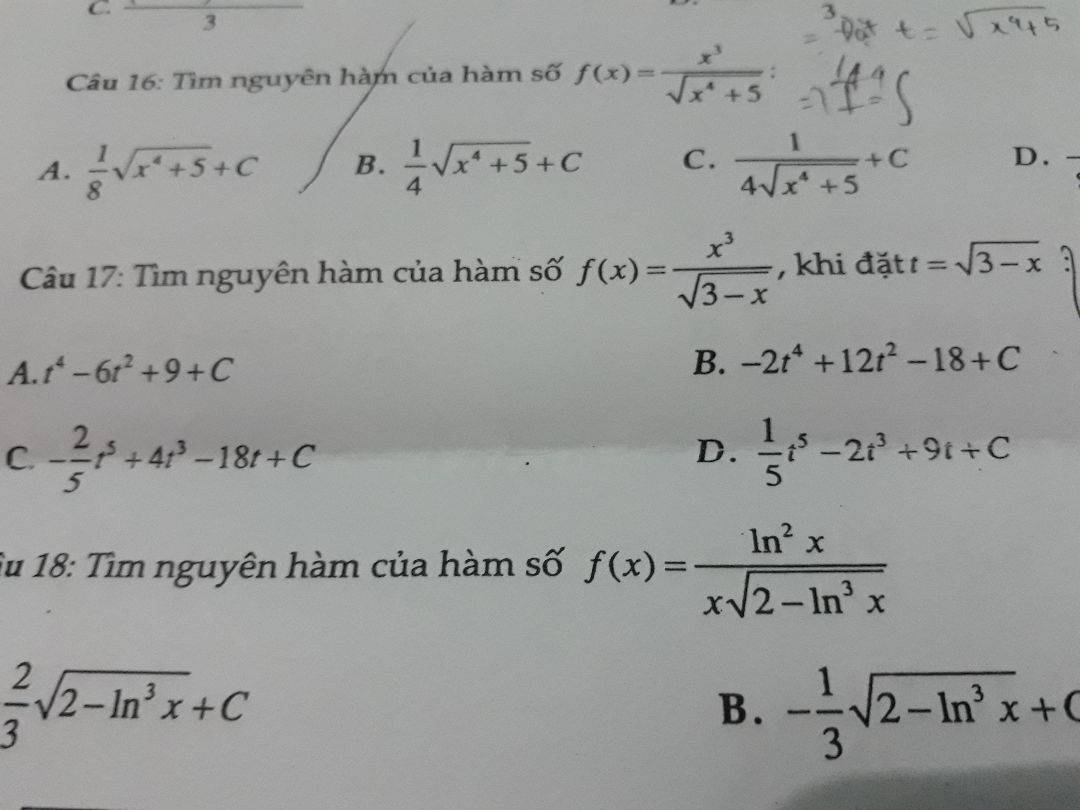 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Tính tích phân từ 1 đến e của (1+ln^3x)/xdx
bởi Mai Thị MInh Thư
 06/11/2019
Câu I giải ntn
06/11/2019
Câu I giải ntn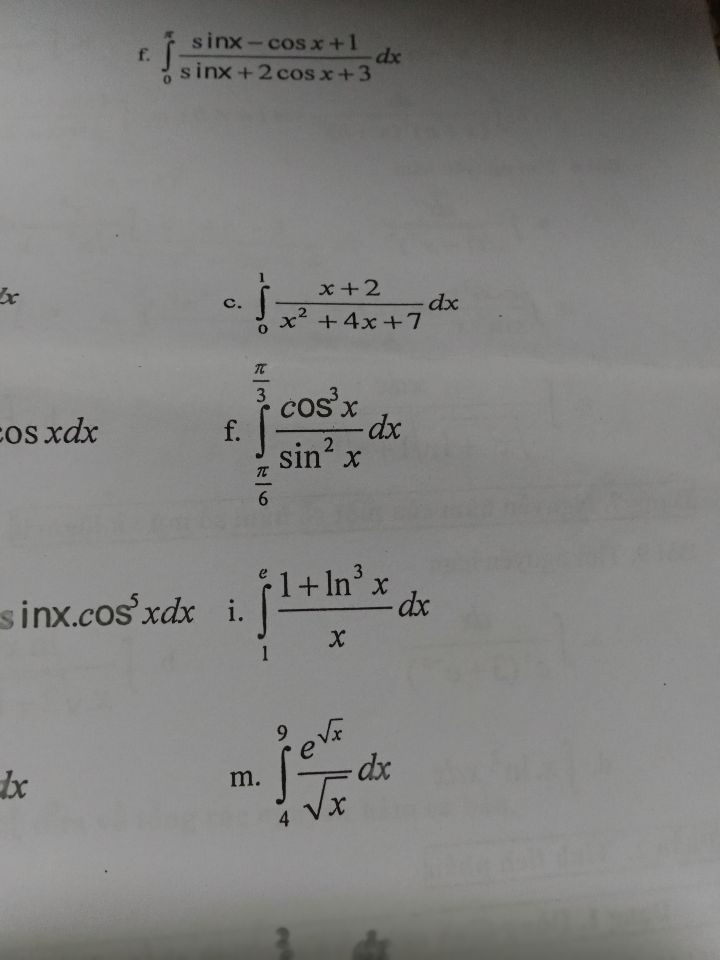 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Tính tích phân từ 0 đến pi của (co2t+2sint/2)dt
bởi Nguyễn Minh Tây
 13/10/2019
13/10/2019
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -

 Biết F(x) là nguyên hàm của f(x)=5^x.ln5 thỏa F(0)=5. Tính F(1)Theo dõi (1) 3 Trả lời
Biết F(x) là nguyên hàm của f(x)=5^x.ln5 thỏa F(0)=5. Tính F(1)Theo dõi (1) 3 Trả lời -


Tính tích phân từ pi/4 đến pi/2 của dx/sin^2 x
bởi Ánh Phạm
 21/06/2019
Câu 28
21/06/2019
Câu 28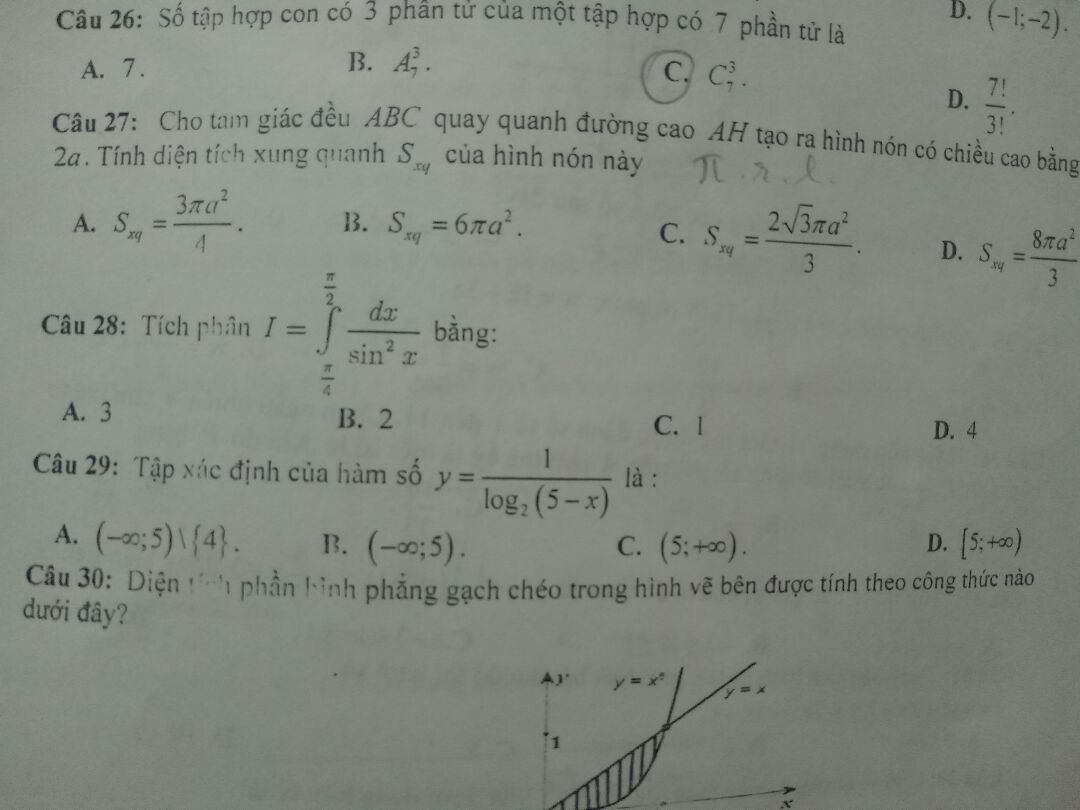 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm công thức tính thể tích khối tròn xoay tạo thành khi hình (H) quanh trục Ox
bởi Trần Xuân Hương
 19/06/2019
Mọi người ơi giúp mình câu 14 với ạ
19/06/2019
Mọi người ơi giúp mình câu 14 với ạ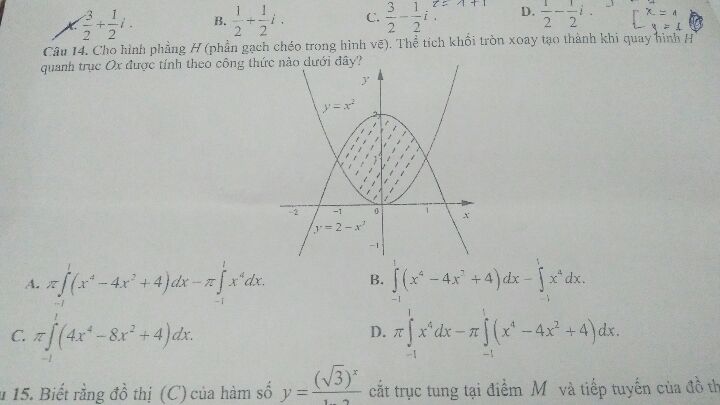 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính S=a+b biết tích phân từ 0 đến pi/4 của (5sinx+cosx)/(sinx+cosx)dx=a.pi+ln b
bởi Trần Quỳnh
 17/06/2019
Cái này bạn nào biết bấm máy không nhỉ ? Mình cũng xem youtube rồi mà không có dạng này hiccc
17/06/2019
Cái này bạn nào biết bấm máy không nhỉ ? Mình cũng xem youtube rồi mà không có dạng này hiccc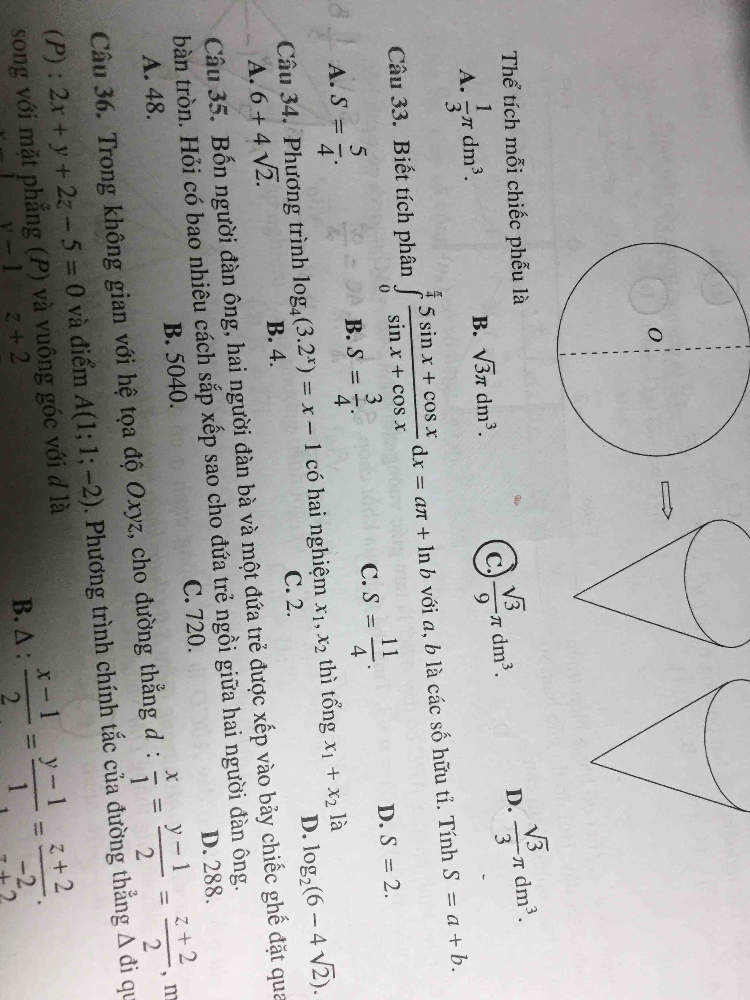 Theo dõi (0) 10 Trả lời
Theo dõi (0) 10 Trả lời -

 Câu 35 làm sao ạ?
Câu 35 làm sao ạ?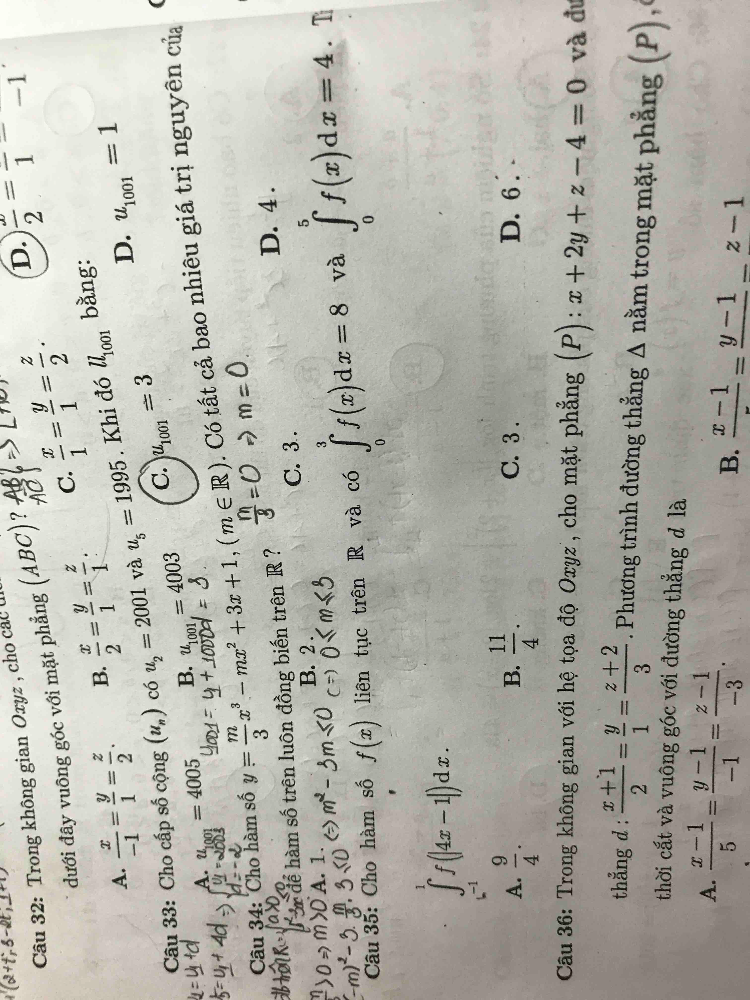 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính giá trị của S=2a+3b+c biết tích phân từ 1 đến 2 của ln/x^2 dx=aln2+b/c
bởi Trần Tuấn
 06/06/2019
06/06/2019
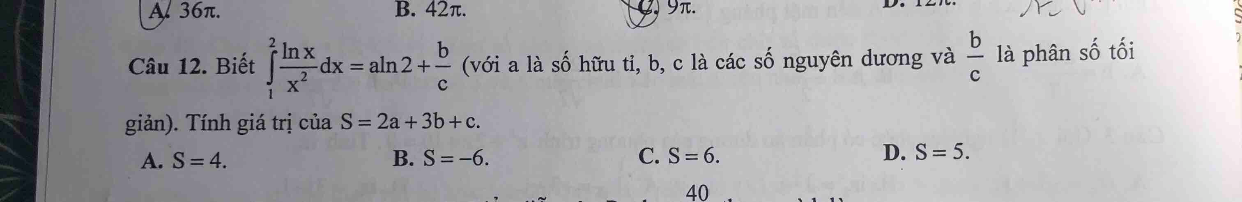 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời



