Giải bài 3.23 tr 172 SBT Toán 12
Đặt \({I_n} = \int \limits_0^{\frac{\pi }{2}} {\sin ^n}xdx,n \in {N^ * }.\)
a) Chứng minh rằng \({I_n} = \frac{{n - 1}}{n}{I_{n - 2}},n > 2\)
b) Tính và
Hướng dẫn giải chi tiết
a) Xét với n > 2, ta có:
\({I_n} = \mathop \smallint \limits_0^{\frac{\pi }{2}} {\sin ^{n - 1}}x\sin xdx,n \in {N^ * }.\)
Đặt \(\left\{ \begin{array}{l}
u = {\sin ^{n - 1}}x\\
dv = \sin xdx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = (n - 1){\sin ^{n - 2}}x.\cos xdv\\
v = - \cos x
\end{array} \right.\)
Khi đó:
\(\begin{array}{l}
{I_n} = \left. { - {{\sin }^{n - 1}}x.\cos x} \right|_0^{\frac{\pi }{2}} + \left( {n - 1} \right)\int\limits_0^{\frac{\pi }{2}} {{{\sin }^{n - 2}}x{{\cos }^2}xdx} \\
= \left( {n - 1} \right)\int\limits_0^{\frac{\pi }{2}} {{{\sin }^{n - 2}}x\left( {1 - {{\sin }^2}x} \right)dx} \\
= \left( {n - 1} \right)\left( {{I_{n - 2}} - {I_n}} \right)\\
\Rightarrow {I_n} = \left( {n - 1} \right){I_{n - 2}} - \left( {n - 1} \right){I_n}\\
\Rightarrow {I_n} = \frac{{n - 1}}{n}{I_{n - 2}}
\end{array}\)
b)
\(\begin{array}{l}
{I_3} = \frac{2}{3}{I_1} = \frac{2}{3}\int\limits_0^{\frac{\pi }{2}} {\sin xdx = - \frac{2}{3}\left. {\cos x} \right|_0^{\frac{\pi }{2}}} = \frac{2}{3}\\
{I_5} = \frac{4}{5}{I_3} = \frac{4}{5}.\frac{2}{3} = \frac{8}{{15}}
\end{array}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.21 trang 172 SBT Toán 12
Bài tập 3.22 trang 172 SBT Toán 12
Bài tập 3.24 trang 172 SBT Toán 12
Bài tập 3.25 trang 173 SBT Toán 12
Bài tập 3.26 trang 173 SBT Toán 12
Bài tập 3.28 trang 173 SBT Toán 12
Bài tập 3.27 trang 173 SBT Toán 12
Bài tập 3.29 trang 173 SBT Toán 12
Bài tập 3.30 trang 173 SBT Toán 12
Bài tập 10 trang 152 SGK Toán 12 NC
Bài tập 11 trang 152 SGK Toán 12 NC
Bài tập 12 trang 153 SGK Toán 12 NC
Bài tập 13 trang 153 SGK Toán 12 NC
Bài tập 14 trang 153 SGK Toán 12 NC
Bài tập 15 trang 153 SGK Toán 12 NC
Bài tập 16 trang 153 SGK Toán 12 NC
Bài tập 17 trang 161 SGK Toán 12 NC
Bài tập 18 trang 161 SGK Toán 12 NC
Bài tập 19 trang 161 SGK Toán 12 NC
Bài tập 20 trang 161 SGK Toán 12 NC
Bài tập 21 trang 161 SGK Toán 12 NC
Bài tập 22 trang 162 SGK Toán 12 NC
Bài tập 23 trang 162 SGK Toán 12 NC
-


Tính tích phân từ 0 đến 2 của căn (4-x^2)dx
bởi Anh Trần Thị Mỹ
 19/04/2020
19/04/2020
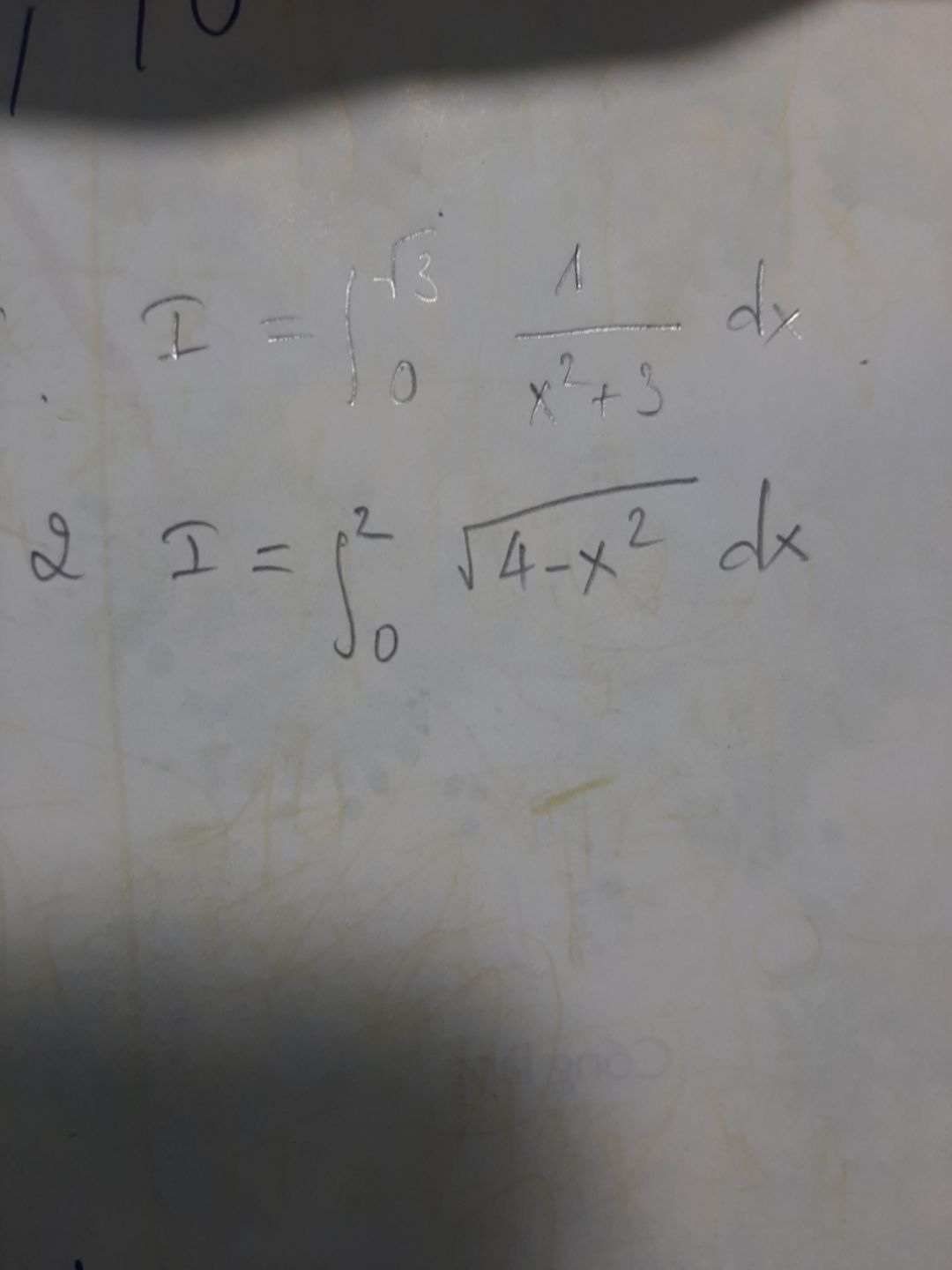 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính tích phân từ 0 đến 1 của (x+1)^2e^2xdx
bởi Gyun Kiến
 18/04/2020
18/04/2020
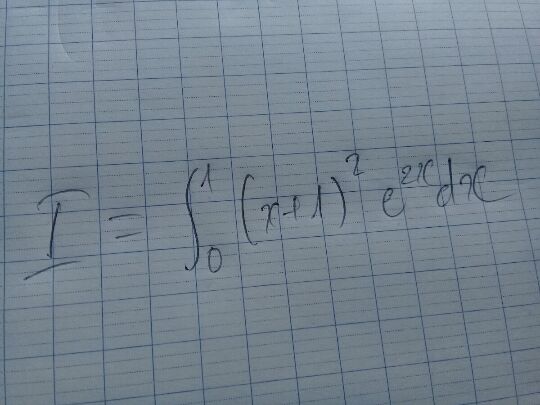 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 /sinx/dx
/sinx/dx Theo dõi (0) 9 Trả lời
Theo dõi (0) 9 Trả lời -


Tính tích phân từ -15 đến 15 của |x^20-9x+18|dx
bởi Minh Huệ
 16/04/2020
16/04/2020
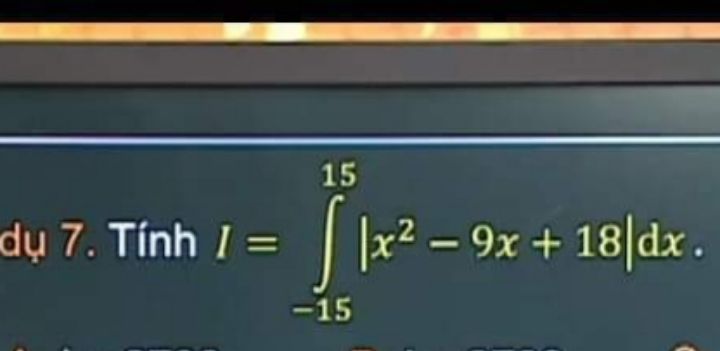 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -
ADMICRO


Tìm mệnh đề đúng trong các mệnh đề
bởi Nguyễn Nhii
 15/04/2020
15/04/2020
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tính tích phân từ 0 đến 4 của (x^2-6x+9)dx
bởi Anh Trần Thị Mỹ
 14/04/2020
14/04/2020
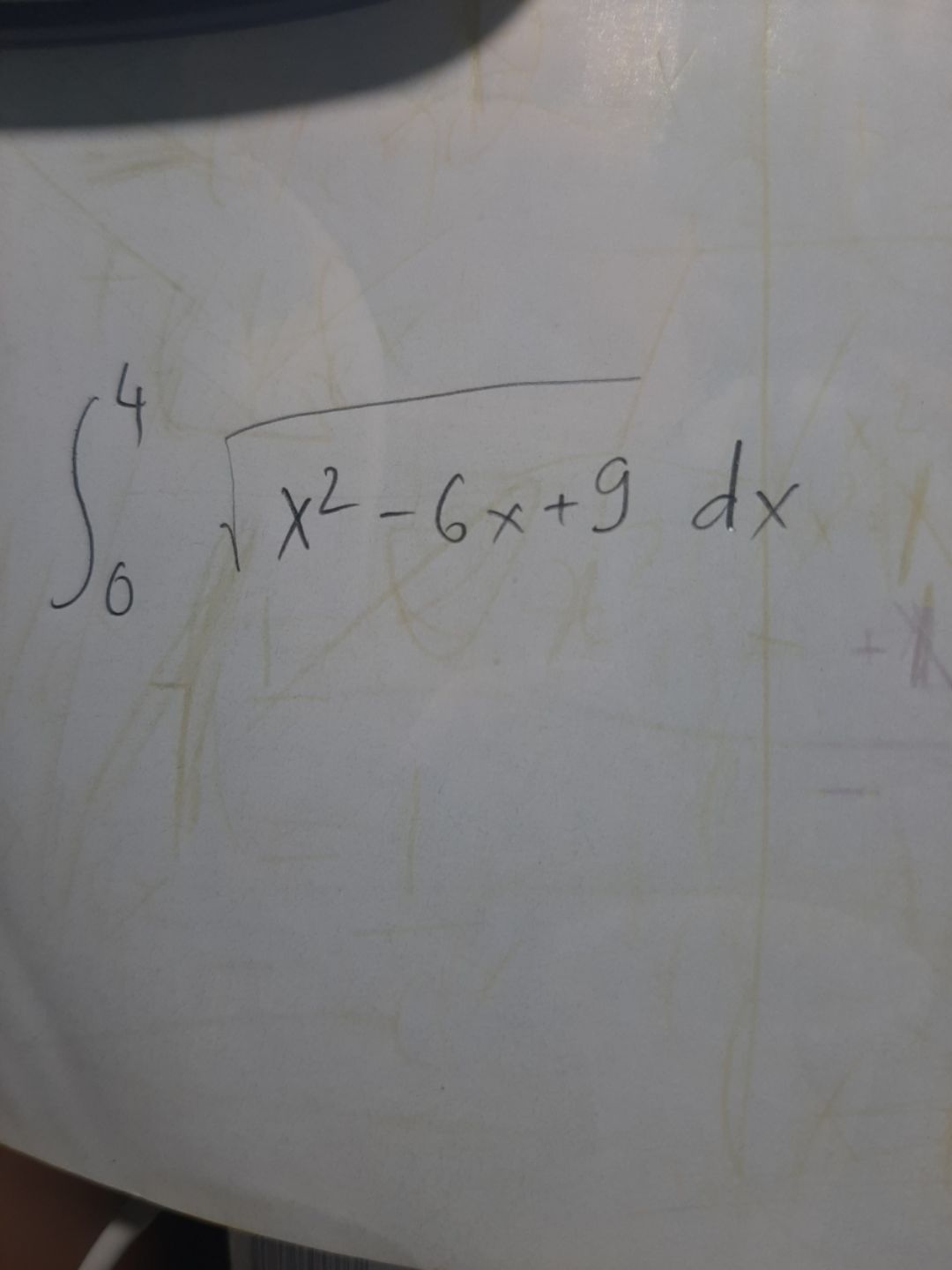 Theo dõi (1) 7 Trả lời
Theo dõi (1) 7 Trả lời -


Tích phân 0 đến 1 của căn(3x+1)dx
bởi Anh Trần Thị Mỹ
 14/04/2020
14/04/2020
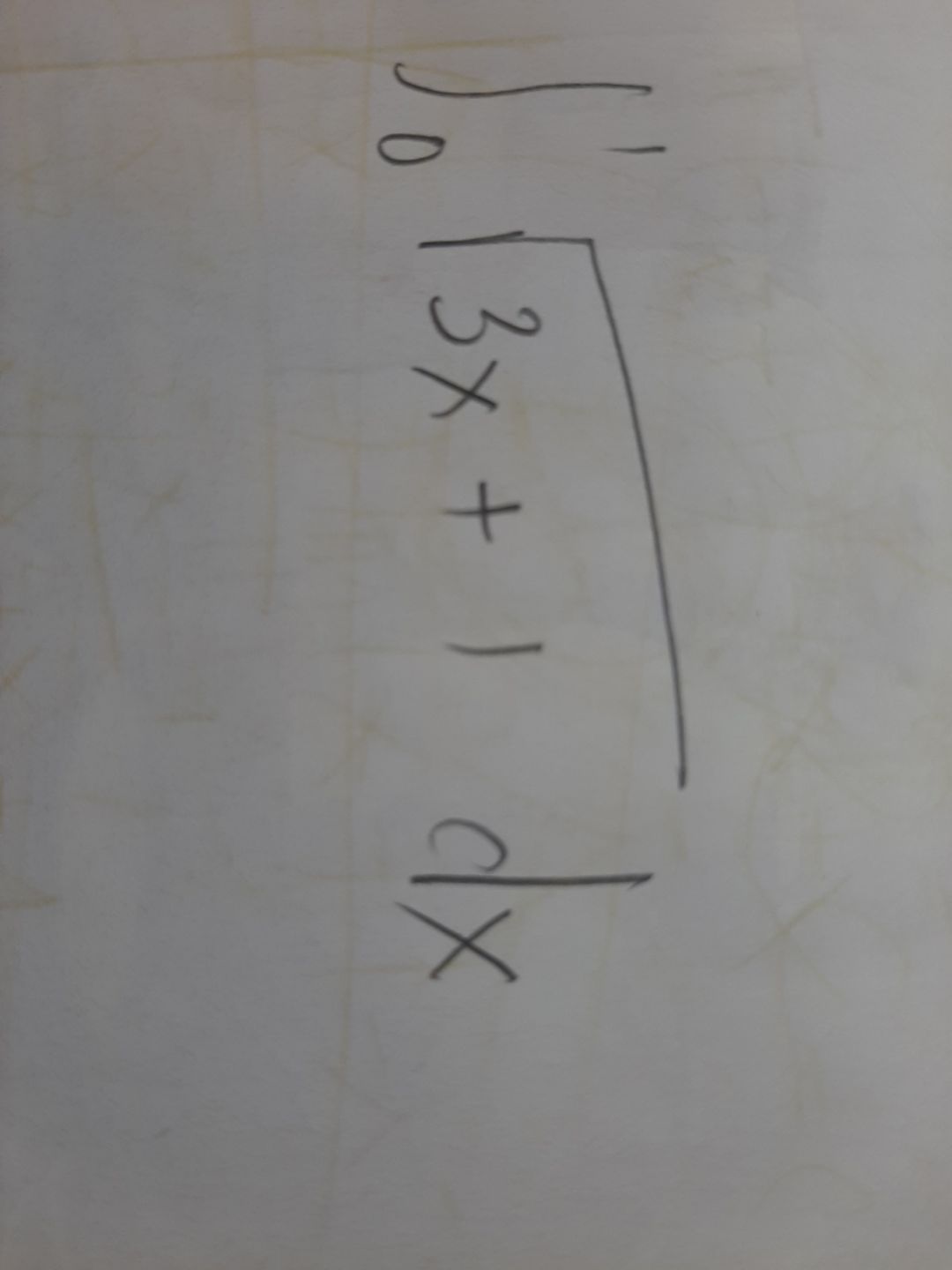 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tính tích phân từ 1 đến 2 của (x+2)^2017/x^2019
bởi vũ thị thúy
 14/04/2020
14/04/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính tích phân từ 0 đến 1 của x/(x^2+1)
bởi Hoa Mai
 14/04/2020
14/04/2020
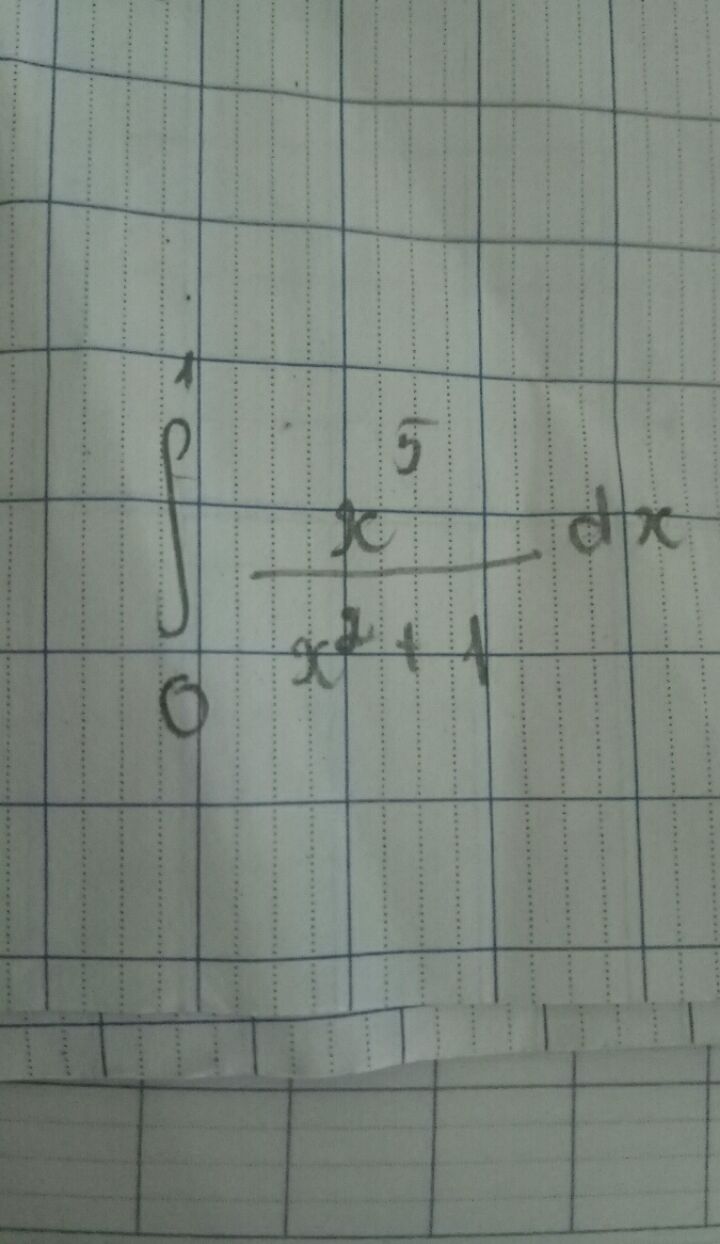 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hàm số f(×) thỏa f'(×)= e^3x và f(0)=1, tính I
bởi Tin An
 13/04/2020
Cho em hỏi câu 3 với câu 4 làm như thế nào vậy ạ?Em xin cảm ơn!
13/04/2020
Cho em hỏi câu 3 với câu 4 làm như thế nào vậy ạ?Em xin cảm ơn! Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Tính tích phân từ 0 đến 4 của x.căn (1+2x)dx
bởi Vân Anhh Tran
 13/04/2020
Chỉ mình các câu này vs ạ
13/04/2020
Chỉ mình các câu này vs ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính tích phân từ 3 đến 4 của (3x^2+6x-2)dx
bởi Vân Anhh Tran
 13/04/2020
Chỉ mình mấy câu này vs ạ
13/04/2020
Chỉ mình mấy câu này vs ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải cầu giúp mình
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính tích phân từ 0 đến 4 của x*ln(2x+1)
bởi Là Em
 08/04/2020
Tích phân từ 0 đến 4của x*ln(2x 1)Theo dõi (0) 7 Trả lời
08/04/2020
Tích phân từ 0 đến 4của x*ln(2x 1)Theo dõi (0) 7 Trả lời -


Tính tích phân của căn(1-x^2)dx cận từ 0 đến 1
bởi Võ Thị Mộng Thùy
 05/04/2020
Giải giúp e câu 151 với ạ
05/04/2020
Giải giúp e câu 151 với ạ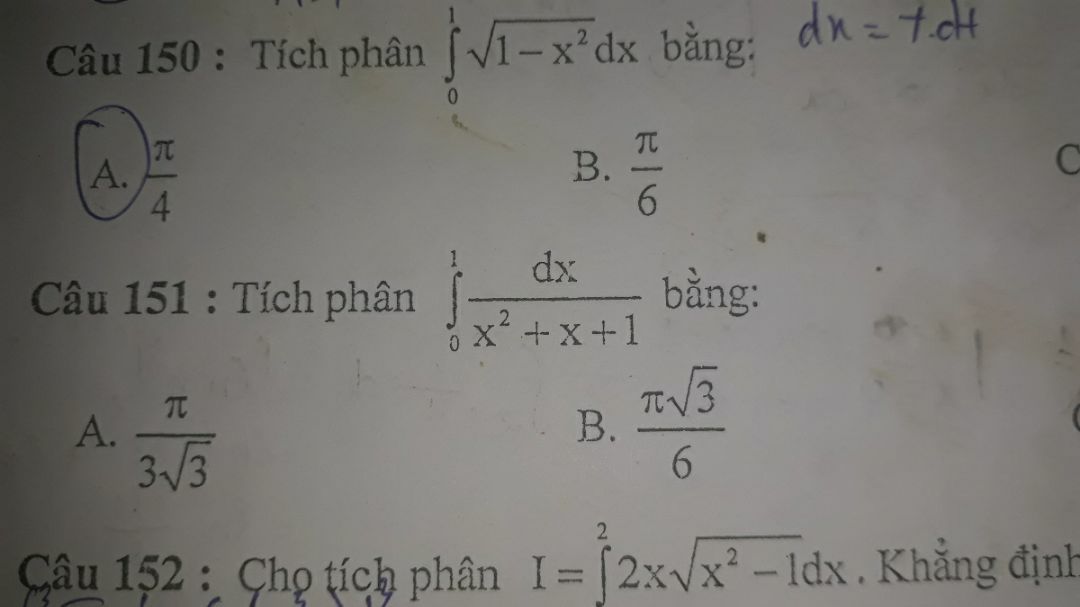 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Tính tích phân từ 0 đến 1 của f(x)dx
bởi Hoàng Thị Bình
 04/04/2020
04/04/2020
Giải giúp mình câu này với ạ
Cho hàm số f(x) có đạo hàm liên tục trên đoạn từ 0;1. Thỏa mãn f(0)=0, f(1)=1 và tích phân từ 0 đến 1 của ((f'(x))^2/e^x)dx =1/e-1. Tính tích phân từ 0 đến 1 của f(x)dx
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 10 Trả lời
Theo dõi (0) 10 Trả lời


