Giải bài 3.62 tr 168 SBT Hình học 10
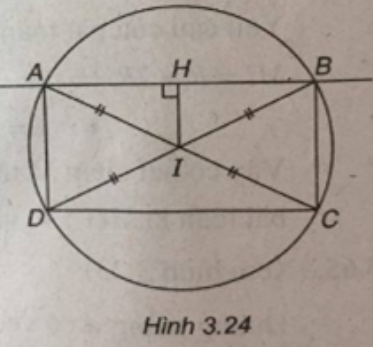
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có tâm \(I\left( {\frac{1}{2};0} \right)\) phương trình đường thẳng AB là : x - 2y + 2 = 0 và AB = 2AD. Tìm tọa độ các đỉnh A, B, C, D biết rằng đỉnh A có hoành độ âm.
Hướng dẫn giải chi tiết
Ta có : \(IH = d\left( {I;AB} \right) = \frac{{\left| {\frac{1}{2} - 2.0} \right|}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2}} }} = \frac{{\sqrt 5 }}{2}\)
\( \Rightarrow AD = \sqrt 5 ,IA = IB = \frac{5}{2}\)
Do đó A, B là các giao điểm của đường thẳng AB với đường tròn tâm I và bán kính \(R = \frac{5}{2}\).
Vậy tọa độ A, B là nghiệm của hệ :
\(\left\{ \begin{array}{l}
x - 2y + 2 = 0\\
{\left( {x - \frac{1}{2}} \right)^2} + {y^2} = {\left( {\frac{5}{2}} \right)^2}
\end{array} \right.\)
Giải hệ ta được A(-2, 0), B(2; 2) (vì xA < 0) ⇒ C(3; 0), D(-1; -2)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 3 trang 118 SGK Hình học 10 NC
Bài tập 4 trang 118 SGK Hình học 10 NC
Bài tập 5 trang 118 SGK Hình học 10 NC
Bài tập 6 trang 119 SGK Hình học 10 NC
Bài tập 7 trang 119 SGK Hình học 10 NC
Bài tập 8 trang 119 SGK Hình học 10 NC
Bài tập 9 trang 119 SGK Hình học 10 NC
Bài tập 10 trang 119 SGK Hình học 10 NC
Bài tập 11 trang 119 SGK Hình học 10 NC
Bài tập 12 trang 119 SGK Hình học 10 NC
Bài tập 13 trang 120 SGK Hình học 10 NC
Bài tập 14 trang 120 SGK Hình học 10 NC
Bài tập 3.37 trang 164 SBT Hình học 10
Bài tập 3.38 trang 165 SBT Hình học 10
Bài tập 3.39 trang 165 SBT Hình học 10
Bài tập 3.40 trang 165 SBT Hình học 10
Bài tập 3.41 trang 165 SBT Hình học 10
Bài tập 3.42 trang 165 SBT Hình học 10
Bài tập 3.43 trang 165 SBT Hình học 10
Bài tập 3.44 trang 165 SBT Hình học 10
Bài tập 3.45 trang 165 SBT Hình học 10
Bài tập 3.46 trang 166 SBT Hình học 10
Bài tập 3.47 trang 166 SBT Hình học 10
Bài tập 3.48 trang 166 SBT Hình học 10
Bài tập 3.49 trang 166 SBT Hình học 10
Bài tập 3.50 trang 166 SBT Hình học 10
Bài tập 3.51 trang 166 SBT Hình học 10
Bài tập 3.52 trang 167 SBT Hình học 10
Bài tập 3.53 trang 167 SBT Hình học 10
Bài tập 3.54 trang 167 SBT Hình học 10
Bài tập 3.55 trang 167 SBT Hình học 10
Bài tập 3.56 trang 167 SBT Hình học 10
Bài tập 3.57 trang 167 SBT Hình học 10
Bài tập 3.58 trang 167 SBT Hình học 10
Bài tập 3.59 trang 167 SBT Hình học 10
Bài tập 3.60 trang 167 SBT Hình học 10
Bài tập 3.61 trang 168 SBT Hình học 10
Bài tập 1 trang 120 SGK Hình học 10 NC
Bài tập 2 trang 120 SGK Hình học 10 NC
Bài tập 3 trang 120 SGK Hình học 10 NC
Bài tập 3.63 trang 168 SBT Hình học 10
Bài tập 4 trang 120 SGK Hình học 10 NC
Bài tập 5 trang 120 SGK Hình học 10 NC
Bài tập 3.64 trang 168 SBT Hình học 10
Bài tập 3.65 trang 168 SBT Hình học 10
Bài tập 3.66 trang 168 SBT Hình học 10
Bài tập 3.67 trang 168 SBT Hình học 10
Bài tập 6 trang 121 SGK Hình học 10 NC
Bài tập 7 trang 121 SGK Hình học 10 NC
Bài tập 8 trang 121 SGK Hình học 10 NC
Bài tập 9 trang 121 SGK Hình học 10 NC
Bài tập 10 trang 121 SGK Hình học 10 NC
Bài tập 11 trang 121 SGK Hình học 10 NC
Bài tập 12 trang 121 SGK Hình học 10 NC
Bài tập 13 trang 122 SGK Hình học 10 NC
Bài tập 14 trang 122 SGK Hình học 10 NC
Bài tập 15 trang 122 SGK Hình học 10 NC
Bài tập 16 trang 122 SGK Hình học 10 NC
Bài tập 17 trang 122 SGK Hình học 10 NC
Bài tập 18 trang 123 SGK Hình học 10 NC
Bài tập 3.68 trang 169 SBT Hình học 10
Bài tập 19 trang 123 SGK Hình học 10 NC
Bài tập 3.69 trang 169 SBT Hình học 10
Bài tập 20 trang 123 SGK Hình học 10 NC
Bài tập 3.70 trang 169 SBT Hình học 10
Bài tập 21 trang 123 SBT Hình học 10
Bài tập 3.71 trang 169 SBT Hình học 10
Bài tập 22 trang 123 SGK Hình học 10 NC
Bài tập 3.72 trang 169 SBT Hình học 10
Bài tập 23 trang 123 SGK Hình học 10 NC
Bài tập 3.73 trang 169 SBT Hình học 10
Bài tập 24 trang 123 SGK Hình học 10 NC
Bài tập 3.74 trang 169 SBT Hình học 10
Bài tập 3.75 trang 169 SBT Hình học 10
Bài tập 3.76 trang 170 SBT Hình học 10
Bài tập 3.77 trang 170 SBT Hình học 10
Bài tập 3.78 trang 170 SBT Hình học 10
Bài tập 3.79 trang 170 SBT Hình học 10
Bài tập 3.80 trang 170 SBT Hình học 10
Bài tập 3.81 trang 170 SBT Hình học 10
Bài tập 3.82 trang 170 SBT Hình học 10
Bài tập 3.83 trang 170 SBT Hình học 10
Bài tập 3.84 trang 171 SBT Hình học 10
Bài tập 3.85 trang 171 SBT Hình học 10
Bài tập 3.86 trang 171 SBT Hình học 10
Bài tập 3.87 trang 171 SBT Hình học 10
Bài tập 3.88 trang 171 SBT Hình học 10
Bài tập 3.89 trang 171 SBT Hình học 10
Bài tập 3.90 trang 171 SBT Hình học 10
Bài tập 3.91 trang 171 SBT Hình học 10
Bài tập 3.92 trang 172 SBT Hình học 10
Bài tập 3.93 trang 172 SBT Hình học 10
Bài tập 1 trang 93 SGK Hình học 10
Bài tập 2 trang 93 SGK Hình học 10
Bài tập 3 trang 93 SGK Hình học 10
Bài tập 4 trang 93 SGK Hình học 10
Bài tập 5 trang 93 SGK Hình học 10
Bài tập 6 trang 93 SGK Hình học 10
-


Cho tam giác ABC có A(-4; 5), H(-3;3), O(0;0) lần lượt là đỉnh, trực tâm và tâm đường tròn ngoại tiếp
bởi Dương Minh Tuấn
 08/02/2017
08/02/2017
Trong mặt phẳng Oxy, cho tam giác ABC có A(-4; 5), H(-3;3), O(0;0) lần lượt là đỉnh, trực tâm và tâm đường tròn ngoại tiếp tam giác ABC. Tìm tọa độ hai đỉnh B và C.
Theo dõi (0) 1 Trả lời -


Tìm tọa độ các đỉnh của hình chữ nhật
bởi Nguyễn Trà Giang
 08/02/2017
08/02/2017
Trong mặt phẳng với hệ trục tọa độ Oxy cho hình chữ nhật ABCD có diện tích bằng 12, tâm I là giao điểm của đường thẳng \(d_{1}\): x - y - 3 = 0 và \(d_{2}\): x + y - 6 = 0. Trung điểm của một cạnh là giao điểm của \(d_{1}\) với trục Ox. Tìm tọa độ các đỉnh của hình chữ nhật.
Theo dõi (0) 1 Trả lời -


Trong mặt phẳng tọa độ Oxy, cho hình thang ABCD vuông tại C, D có BC = 2AD = 2AD
bởi Nguyễn Bảo Trâm
 07/02/2017
07/02/2017
Trong mặt phẳng tọa độ Oxy, cho hình thang ABCD vuông tại C, D có BC = 2AD = 2AD. Đỉnh C(3; 3), đỉnh A nằm trên đường thẳng d: 3x + y - 2 = 0, phương trình đường thẳng DM: x - y - 2 = 0 với M là điểm thỏa mãn \(\overrightarrow{BC}=-4\overrightarrow{CM}\). Xác định tọa độ các điểm A, D, B
Theo dõi (0) 1 Trả lời -


Xác định tọa độ các đỉnh của hình vuông ABCD biết khoảng cách từ điểm H đến cạnh CD bằng\(\small \frac{12\sqrt{2}}{13}\
bởi Thiên Mai
 07/02/2017
07/02/2017
Trong mặt phẳng với hệ trục tọa độ Oxy, cho hình vuông ABCD. Điểm N(1;-2) thỏa mãn \(\small 2\overrightarrow{NB}+\overrightarrow{NC}=\vec{0}\) và điểm M(3; 6) thuộc đường thẳng chứa cạnh AD. Gọi H là hình chiếu vuông góc của đỉnh A xuống đường thẳng DN. Xác định tọa độ các đỉnh của hình vuông ABCD biết khoảng cách từ điểm H đến cạnh CD bằng\(\small \frac{12\sqrt{2}}{13}\) và định A có hoành độ là một số nguyên lớn hơn -2.
Theo dõi (0) 1 Trả lời