Bài tập 3.62 trang 133 SBT Toán 12

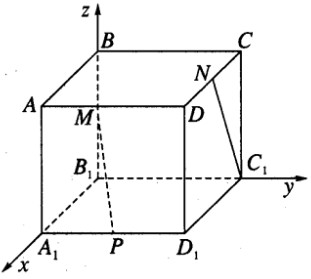
Ta chọn hệ trục tọa độ như sau:

B₁ là gốc tọa độ

\(\overrightarrow {{B_1}{A_1}}  = \vec i,\overrightarrow {{B_1}{C_1}}  = \vec j,\overrightarrow {{B_1}B}  = \vec k\) 

Trong hệ trục vừa chọn, ta có B₁(0; 0; 0), B(0; 0; 1), A₁(1; 0; 0), D₁(1; 1; 0), C(0; 1; 1), D(1; 1; 1), C₁(0; 1; 0).

Suy ra M(0;0;12), P(1;12;0), N(12;1;1)

Ta có \(\overrightarrow {MP}  = (1;\frac{1}{2}; - \frac{1}{2});\overrightarrow {{C_1}N}  = (\frac{1}{2};0;1)\)

Gọi (α) là mặt phẳng chứa C₁N và song song với MP. (α) có vecto pháp tuyến là \(\vec n = (\frac{1}{2}; - \frac{5}{4}; - \frac{1}{4})\) hay \({\vec n\prime } = (2; - 5; - 1)\)

Phương trình của (α) là:

\(2x-5(y-1)-z = 0\) hay \(2x-5y-z + 5 = 0\)

Ta có:

\(\begin{array}{l}
d(MP,{C_1}N) = d(M,(\alpha ))\\
 = \frac{{| - \frac{1}{2} + 5|}}{{\sqrt {25 + 4 + 1} }} = \frac{9}{{2\sqrt {30} }}
\end{array}\)

Ta có:  

\(\cos (\widehat {MP,{C_1}N}) = \frac{{|\overrightarrow {MP} .\overrightarrow {{C_1}N} |}}{{|\overrightarrow {MP} |.|\overrightarrow {{C_1}N} |}} = 0\)

Vậy \((\widehat {MP,{C_1}N}) = {90^0}\)

-- Mod Toán 12 HỌC247