Ôn tập Vật Lý 12 Chương 3 Dòng Điện Xoay Chiều

Đề cương Ôn tập Vật Lý 12 Chương 3

A. Tóm tắt lý thuyết

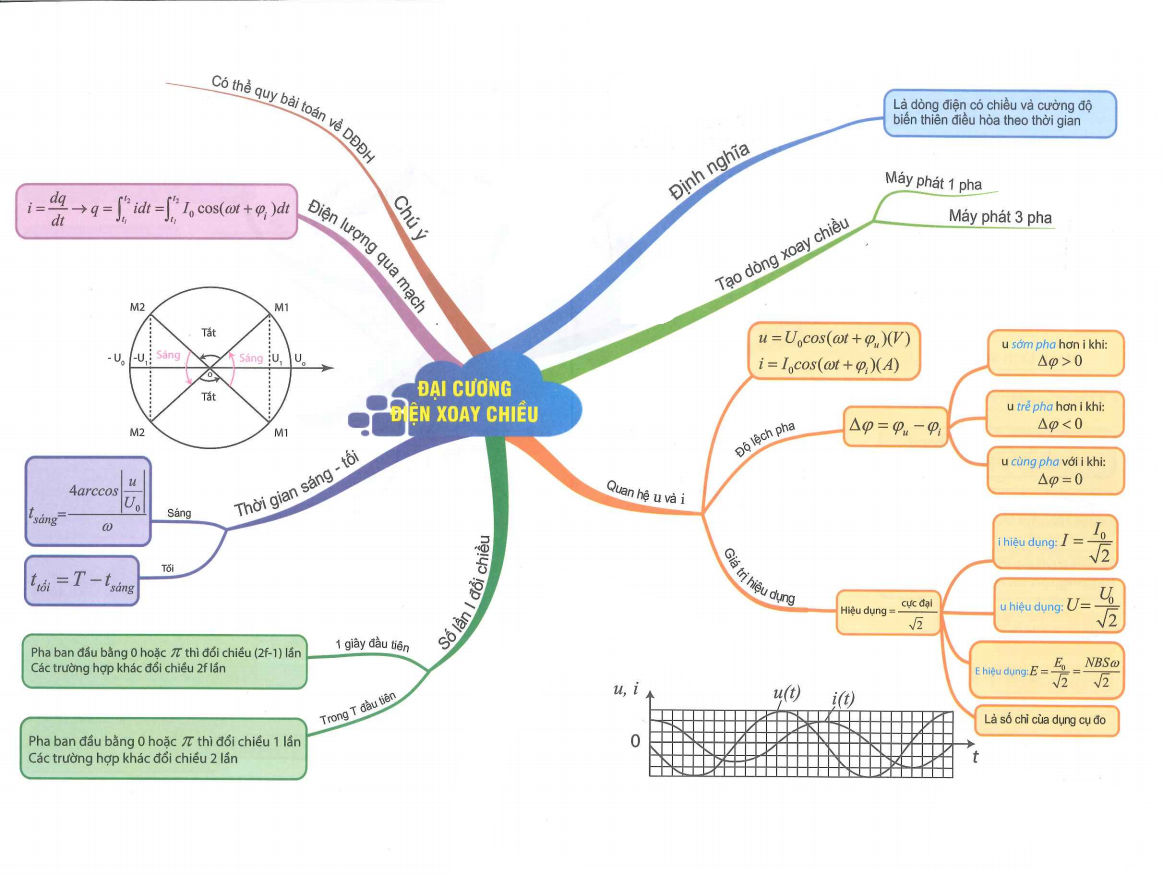
1. Đại cương về dòng điện xoay chiều

1.1. Cách tạo ra suất điện động xoay chiều:

a.Từ thông gởi qua khung dây :

-Từ thông gửi qua khung dây dẫn gồm N vòng dây có diện tích S quay trong từ trường đều \(\overrightarrow B \). 

-Biểu thức từ thông của khung: \(\Phi  = N.B.S.\cos \omega t = \Phi o.\cos \omega t\)

      (Với \(\Phi \)= L I  và Hệ số tự cảm  L = 4\(\pi \).10^-7 N².S/l )

 Đơn vị : +\(\Phi \): Vêbe(Wb);                

               + S: Là diện tích một vòng dây (S: m²);

               + N: Số vòng dây của khung

               +\(\overrightarrow B \): Véc tơ cảm ứng từ của từ trường đều .B:Tesla(T) 

               +\(\omega \): Vận tốc góc không đổi của khung dây

            ( Chọn gốc thời gian t=0 lúc ( \(\overrightarrow n ,\overrightarrow B ) = \) 0⁰)

 -Chu kì và tần số của khung : \(T = \frac{{2\pi }}{\omega };f = \frac{1}{T}\)

b. Suất điện động xoay chiều:

- Biểu thức của suất điện động cảm ứng tức thời: e = \(\frac{{ - \Delta \Phi }}{{\Delta t}} =  - \Phi ' = \omega NBS.\sin \omega t = {E_0}c{\rm{os(}}\omega t - \frac{\pi }{2})\) 

    Đơn vị :e,E₀ (V)

1.2. Điện áp xoay chiều -Dòng điện xoay chiều.

a. Biểu thức điện áp tức thời: Nếu nối hai đầu khung dây với mạch ngoài thành mạch kín thì biểu thức điện áp tức thời mạch ngoài là: u=e-ir

Tổng quát : \(\varphi u\)   ( \(\varphi u\) là pha ban đầu của  điện áp )  

b. Khái niệm về dòng điện xoay chiều

- Là dòng điện có cường độ biến thiên tuần hoàn với thời gian theo quy luật của hàm số sin hay cosin, với dạng tổng quát:        i = I₀­\(c{\rm{os}}(\omega t + \varphi i)\) 

* i: giá trị của cường độ dòng điện tại thời điểm t, được gọi là giá trị tức thời của i (cường độ tức thời).

* I₀ > 0: giá trị cực đại của i (cường độ cực đại).  

* w > 0: tần số góc.

 f: tần số của i. T: chu kì của i.

* (wt + j): pha của i.

* \(\varphi i\) là pha ban đầu của dòng điện)

c. Độ lệch pha giữa điện áp u và cường độ dòng điện i:
Đại lượng : \(\varphi  = {\varphi _u} - \varphi i\) gọi là độ lệch pha của u so với i.

Nếu \(\varphi \) >0 thì u sớm pha (nhanh pha) so với i.

Nếu \(\varphi \) <0 thì u trễ pha (chậm pha) so với i.

Nếu \(\varphi \) = 0 thì u đồng pha (cùng pha) so với i.

d. Giá trị hiệu dụng  :Dòng điện xoay chiều cũng có tác dụng toả nhiệt như dòng điện một chiều.Xét về mặt toả nhiệt trong một thời gian dài thì dòng điện xoay chiều  i = I0­\(c{\rm{os}}(\omega t + \varphi i)\)  tương đương với dòng điện một chiều có cường độ không đổi có cường độ bằng \(\frac{{{I_0}}}{{\sqrt 2 }}\).

Các giá trị hiệu dụng của dòng điện xoay chiều:

- Giá trị hiệu dụng : + Cường độ dòng điện hiệu dụng:I = \(\frac{{{I_0}}}{{\sqrt 2 }}\)

                            + Hiệu điện thế hiệu dụng:    U = \(\frac{{{U_0}}}{{\sqrt 2 }}\)

                            + Suất điện động hiệu dụng:  E = \(\frac{{{E_0}}}{{\sqrt 2 }}\)

*Lý do sử dụng các giá trị hiệu dụng của dòng điện xoay chiều:

-- Khi sử dụng dòng điện xoay chiều, ta không cần quan tâm đến các giá trị tức thời của i và u vì chúng biến thiên rất nhanh, ta cần quan tâm tới tác dụng của nó trong một thời gian dài.

  - Tác dụng nhiệt của dòng điện tỉ lệ với bình phương cường độ dòng điện nên không phụ thuộc vào chiều dòng điện. 

  - Ampe kế đo cường độ dòng điện xoay chiều và vôn kế đo điện áp xoay chiều dựa vào tác dụng nhiệt của dòng điện nên gọi là ampe kế nhiệt và vôn kế nhiệt, số chỉ của chúng là cường độ hiệu dụng và điện áp hiệu dụng của dòng điện xoay chiều.

e. Công suất toả nhiệt trên R khi có ddxc chạy qua :   P=RI²

2. Các mạch điện xoay chiều

2.1. Đoạn mạch chỉ có điện trở thuần:

u_R cùng pha với i : I = \(\frac{{{U_R}}}{R}\)

2.2. Đoạn mạch chỉ có tụ điện C:   

      u_C trễ pha so với i góc \(\frac{\pi }{2}\).

- ĐL ôm:  I  = \(\frac{{{U_C}}}{{{Z_C}}}\); với Z_C =\(\frac{1}{{\omega C}}\)  là dung kháng của tụ điện.

-Đặt điện áp \(u = U\sqrt 2 \cos \omega t\) vào hai đầu một tụ điện thì cường độ dòng điện qua nó có giá trị hiệu dụng là I. Tại thời điểm t, điện áp ở hai đầu tụ điện là u và cường độ dòng điện qua nó là i. Hệ thức liên hệ giữa các đại lượng là :

Ta có: \(\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_{0C}^2}} = 1 \Leftrightarrow \frac{{{i^2}}}{{2{I^2}}} + \frac{{{u^2}}}{{2U_C^2}} = 1\)

⇒ \(\frac{{{u^2}}}{{{U^2}}} + \frac{{{i^2}}}{{{I^2}}} = 2\)

      -Cường độ dòng điện tức thời qua tụ: \(i = I\sqrt 2 \cos (\omega t + \frac{\pi }{2})\)

2.3. Đoạn mạch chỉ có cuộn dây thuần cảm L: u_L sớm pha hơn i góc \(\frac{\pi }{2}\).

    - ĐL ôm:  I =\(\frac{{{U_L}}}{{{Z_L}}}\); với Z_L = wL là cảm kháng của cuộn dây.

-Đặt điện áp \(u = U\sqrt 2 \cos \omega t\) vào hai đầu một cuộn cảm thuần thì cường độ dòng điện qua nó có giá trị hiệu dụng là I. Tại thời điểm t, điện áp ở hai đầu cuộn cảm thuần  là u và cường độ dòng điện qua nó là i. Hệ thức liên hệ giữa các đại lượng là :

           Ta có:    \(\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_{0L}^2}} = 1 \Leftrightarrow \frac{{{i^2}}}{{2{I^2}}} + \frac{{{u^2}}}{{2U_L^2}} = 1\)

⇒  \(\frac{{{u^2}}}{{{U^2}}} + \frac{{{i^2}}}{{{I^2}}} = 2\)        

-Cường độ dòng điện tức thời qua cuộn dây: \(i = I\sqrt 2 \cos (\omega t - \frac{\pi }{2})\)

2.4. Đoạn mạch có R, L, C không phân nhánh:

     +Đặt điện áp \(u = U\sqrt 2 \cos (\omega t + {\varphi _u})\) vào hai đầu mạch

    + Độ lệch pha j giữa u và i xác định theo biểu thức:  tanj = \(\frac{{{Z_L} - {Z_C}}}{R}\)= \(\frac{{\omega L - \frac{1}{{\omega C}}}}{R}\); Với \(\varphi  = {\varphi _u} - {\varphi _i}\)

+ Cường độ hiệu dụng xác định theo định luật Ôm: I =\(\frac{U}{Z}\).

        Với Z = \(\sqrt {{{\rm{R}}^{\rm{2}}}{\rm{ }} + {\rm{ (}}{{\rm{Z}}_{\rm{L}}}{\rm{  -  }}{{\rm{Z}}_{\rm{C}}}{{\rm{)}}^{\rm{2}}}} \)  là tổng trở của đoạn mạch.

         Cường độ dòng điện tức thời qua mạch: \(i = I\sqrt 2 \cos (\omega t + {\varphi _i}) = I\sqrt 2 \cos (\omega t + {\varphi _u} - \varphi )\) 

     + Cộng hưởng điện trong đoạn mạch RLC:  Khi Z_L = Z_C hay w = \(\frac{1}{{\sqrt {LC} }}\)     thì

             I_max = U/R,   P_max = \(\frac{{{U^2}}}{R}\), u cùng pha với i (j = 0).

Khi Z_L > Z_C  thì u nhanh pha hơn i (đoạn mạch có tính cảm kháng).

Khi Z_L < Z_C  thì u trể pha hơn i (đoạn mạch có tính dung kháng).

R tiêu thụ năng lượng dưới dạng toả nhiệt, Z_L và Z_C không tiêu thụ năng lượng điện.

2.5. Đoạn mạch có R, L,r, C không phân nhánh:

+ Đặt điện áp \(u = U\sqrt 2 \cos (\omega t + {\varphi _u})\) vào hai đầu mạch

+ Độ lệch pha j giữa u_AB và i xác định theo biểu thức:

                tanj = \(\frac{{{Z_L} - {Z_C}}}{{R + r}}\)= \(\frac{{\omega L - \frac{1}{{\omega C}}}}{{R + r}}\)  . Với \(\varphi  = {\varphi _u} - {\varphi _i}\)

+ Cường độ hiệu dụng xác định theo định luật Ôm: I =\(\frac{U}{Z}\).

 Với Z = \(\sqrt {{{{\rm{(R + r)}}}^{\rm{2}}}{\rm{ }} + {\rm{ (}}{{\rm{Z}}_{\rm{L}}}{\rm{  -  }}{{\rm{Z}}_{\rm{C}}}{{\rm{)}}^{\rm{2}}}} \)  là tổng trở của đoạn mạch.

         Cường độ dòng điện tức thời qua mạch: \(i = I\sqrt 2 \cos (\omega t + {\varphi _i}) = I\sqrt 2 \cos (\omega t + {\varphi _u} - \varphi )\))

3. Công suất tiêu thụ trong mạch điện xoay chiều

3.1. Công suất mạch điện xoay chiều không phân nhánh RLC

a. Công suất tiêu thụ trong mạch RLC không phân nhánh:

         +Công suất tức thời: P = UIcosj + UIcos(2wt + j)                  (1)

         +Công suất trung bình: P = UIcosj = RI².

         +Công suất tiêu thụ của mạch điện xoay chiều:  \(P = UICos\alpha \)   (2)

         +Hệ số công suất: \(Cos\varphi  = \frac{R}{Z}\) ( \(Cos\varphi\) có giá trị từ 0 đến 1)       (3)

b. Ý nghĩa của hệ số công suất 

+Trường hợp cosj = 1 -> j = 0: mạch chỉ có R, hoặc mạch RLC có cộng hưởng điện

    (Z_L = Z_C) thì: P = Pmax =  UI = \(\frac{{{U^2}}}{R}\).             

+Trường hợp cosj = 0 tức là j = ±\(\frac{\pi }{2}\): Mạch chỉ có L, hoặc C, hoặc có cả L và C mà không có R thì:  P = P_min = 0.

3.2. Công suất tiêu thụ cực đại khi mạch RLC có cộng hưởng.

Nếu giữ không đổi điện áp hiệu dụng U giữa hai đầu đoạn mạch và thay đổi tần số góc w (hoặc thay đổi f, L, C) sao cho \(\omega L = \frac{1}{{\omega C}}\) (hay Z_L=Z_C)  thì có  hiện tượng cộng hưởng điện.

Điều kiện xảy ra hiện tượng cộng hưởng trong mạch RLC nối tiếp:

            Z_L=Z_C; \(\omega L = \frac{1}{{\omega C}}\) (hay ZL=ZC); \(\omega  = \frac{1}{{\sqrt {LC} }}\)                        

­ Lúc mạch có cộng hưởng thì:

Tổng trở:        Z = Z_min = R; U_R = U_Rmax = U   

Cường độ dòng điện: \(I = {{\mathop{\rm I}\nolimits} _{max}} = \frac{U}{R}\)

Công suất của mạch khi có cộng hưởng đạt giá trị cực đại:

                                             \(P = {P_{max}} = \frac{{{U^2}}}{R}\)          

Mạch có cộng hưởng thì điện áp cùng pha với cường độ dòng điện, nghĩa là:

                                             j=0; j_u= j_i ; cosj=1       

Điện áp giữa hai điểm M, B chứa L và C đạt cực tiểu

                                             U_LCmin = 0.                                                              

Lưu ý: L và C mắc liên tiếp nhau

4. Hiện tượng cộng hưởng điện

4.1. Cộng hưởng điện:

Điều kiện: Z_L = Z_{C   <=>} \(\omega L = \frac{1}{{C\omega }}\,\; \Leftrightarrow LC{\omega ^2} = 1\)

+ Cường độ dòng điện trong mạch cực đại: I_max = \(\frac{U}{{{Z_{\min }}}} = \frac{U}{{\rm{R}}} = \frac{{{U_{\rm{R}}}}}{{\rm{R}}}\)

+ Điện áp hiệu dụng: \({U_L} = {U_C} \to {U_{\rm{R}}} = U\);  P= P_MAX =  \(\frac{{{U^2}}}{{\rm{R}}}\)

+ Điện áp và cường độ dòng điện cùng pha ( tức φ = 0 )

+ Hệ số công suất cực đại: cosφ = 1.

4.2. Ứng dụng: tìm L, C, tìm f khi  có Cộng hưởng điện:

+ Số chỉ ampe kế cực đại, hay cường độ dòng điện hiệu dụng đạt giá trị lớn nhất

+ Cường độ dòng điện và điện áp cùng pha, điện áp hiệu dụng: \({U_L} = {U_C} \to {U_{\rm{R}}} = U\); 

+ hệ số công suất cực đại, công suất cực đại....

B. Bài tập minh họa

Bài 1:

Hướng dẫn giải:

Cảm kháng: \({Z_L} = \omega L = 100\pi .\frac{1}{\pi } = 100\Omega \);

Dung kháng: \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{2.10}^{ - 4}}}}{\pi }}} = 50\Omega \)

Tổng trở:   \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}  = \sqrt {{{50}^2} + {{\left( {100 - 50} \right)}^2}}  = 50\sqrt 2 \Omega \)

+ Định luật Ôm :  Với U_o= I_oZ = 5.50\(\sqrt 2 \) = 250\(\sqrt 2 \)V;       

+ Tính độ lệch  pha giữa u hai đầu mạch và i:  \(\tan \varphi  = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{100 - 50}}{{50}} = 1\)

\( \Rightarrow \varphi  = \frac{\pi }{4}\) (rad).

+ Biểu thức điện áp tức thời giữa hai đầu mạch điện:  \(u = 250\sqrt 2 \cos \left( {100\pi t + \frac{\pi }{4}} \right)\) (V).

Bài 2:

Hướng dẫn giải:

Ta có :  \(U = \frac{{{U_o}}}{{\sqrt 2 }} = \frac{{120\sqrt 2 }}{{\sqrt 2 }} = 120\)(V)

 \(I = \frac{{{I_o}}}{{\sqrt 2 }} = \frac{{3\sqrt 2 }}{{\sqrt 2 }} = 3\) (A)

Độ lệch pha:        \(\varphi  = {\varphi _u} - {\varphi _i} =  - \frac{\pi }{4} - \frac{\pi }{{12}} =  - \frac{\pi }{3}\) rad

Vậy công suất của đoạn mạch là:     \(P = UI\cos \varphi  = 120.3.\cos \left( { - \frac{\pi }{3}} \right) = 180\) (W).

Trắc nghiệm Vật Lý 12 Chương 3

• Trắc nghiệm Vật lý 12 Bài 12 Đại cương về dòng điện xoay chiều

• Trắc nghiệm Vật lý 12 Bài 13 Các mạch điện xoay chiều

• Trắc nghiệm Vật lý 12 Bài 14 Mạch có R, L, C mắc nối tiếp

• Trắc nghiệm Vật lý 12 Bài 15 Công suất tiêu thụ của mạch điện xoay chiều

• Trắc nghiệm Vật lý 12 Bài 16 Truyền tải điện năng và máy biến áp

• Trắc nghiệm Vật lý 12 Bài 17 Máy phát điện xoay chiều

• Trắc nghiệm Vật lý 12 Bài 18 Động cơ không đồng bộ ba pha

Đề kiểm tra Vật Lý 12 Chương 3

Đề kiểm tra trắc nghiệm online Chương 3 Vật lý 12 (Thi Online)

Phần này các em được làm trắc nghiệm online trong vòng 45 phút để kiểm tra năng lực và sau đó đối chiếu kết quả và xem đáp án chi tiết từng câu hỏi.

• Đề kiểm tra 1 tiết chương Dòng điện xoay chiều Vật lý 12

• 30 câu trắc nghiệm Công suất điện xoay chiều Vật lý 12 có Video lời giải

• 40 câu trắc nghiệm Dòng điện xoay chiều Vật lý 12 có Video lời giải 

• 30 Bài tập trắc nghiệm Vật lý 12 chương Dòng điện xoay chiều nâng cao

Đề kiểm tra Chương 3 Vật lý 12 (Tải File)

Phần này các em có thể xem online hoặc tải file đề thi về tham khảo gồm đầy đủ câu hỏi và đáp án làm bài.

• Bài tập trắc nghiệm ôn tập chương 3 Điện xoay chiều môn Vật lý 12 có đáp án

• 30 câu trắc nghiệm về Thời gian trong dao động trong mạch điện xoay chiều RLC môn Vật Lý 12 có đáp án

• 35 câu trắc nghiệm Ôn tập về Máy biến áp chương Dòng điện xoay chiều môn Vật Lý 12 có đáp án

• 40 câu trắc nghiệm Luyện tập Nâng cao chương Dòng điện xoay chiều Vật Lý lớp 12 có đáp án

• 40 câu trắc nghiệm Dòng điện xoay chiều Vật lý 12 có Video lời giải

Lý thuyết từng bài chương 3 và hướng dẫn giải bài tập SGK

Lý thuyết các bài học Vật lý 12 Chương 3

• Vật lý 12 Bài 12: Đại cương về dòng điện xoay chiều

• Vật lý 12 Bài 13: Các mạch điện xoay chiều

• Vật lý 12 Bài 14: Mạch có R, L, C mắc nối tiếp

• Vật lý 12 Bài 15: Công suất điện tiêu thụ của mạch điện xoay chiều

• Vật lý 12 Bài 16: Truyền tải điện năng và máy biến áp

• Vật lý 12 Bài 17: Máy phát điện xoay chiều

• Vật lý 12 Bài 18: Động cơ không đồng bộ ba pha

• Vật lý 12 Bài 19: Thực hành Khảo sát đoạn mạch xoay chiều RLC

Hướng dẫn giải Vật lý 12 Chương 3

• Giải bài tập Vật lý 12 Chương 3 Bài 12

• Giải bài tập Vật lý 12 Chương 3 Bài 13

• Giải bài tập Vật lý 12 Chương 3 Bài 14

• Giải bài tập Vật lý 12 Chương 3 Bài 15

• Giải bài tập Vật lý 12 Chương 3 Bài 16

• Giải bài tập Vật lý 12 Chương 3 Bài 17

• Giải bài tập Vật lý 12 Chương 3 Bài 18 

Trên đây là tài liệu Ôn tập Vật lý 12 Chương 3 Dòng Điện Xoay Chiều. Hy vọng rằng tài liệu này sẽ giúp các em ôn tập tốt và hệ thống lại kiến thức Chương 3 hiệu quả hơn. Để thi online và tải file đề thi về máy các em vui lòng đăng nhập vào trang hoc247.net và ấn chọn chức năng "Thi Online" hoặc "Tải về". Ngoài ra, các em còn có thể chia sẻ lên Facebook để giới thiệu bạn bè cùng vào học, tích lũy thêm điểm HP và có cơ hội nhận thêm nhiều phần quà có giá trị từ HỌC247 !