Giải bài 5 tr 80 sách GK Toán Hình lớp 12
Cho tứ diện có các đỉnh là A(5 ; 1 ; 3), B(1 ; 6 ; 2), C(5 ; 0 ; 4), D(4 ; 0 ; 6).
a) Hãy viết các phương trình mặt phẳng (ACD) và (BCD)
b) Hãy viết phương trình mặt phẳng (α) đi qua cạnh AB và song song với cạnh CD.
Hướng dẫn giải chi tiết bài 5
Phương pháp:
Mặt phẳng đi qua 3 điểm A, B, C không thẳng hàng có một VTPT \(\vec{n}=\left [ \overrightarrow{AB};\overrightarrow{AC} \right ]\).
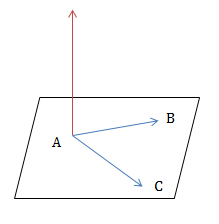
Giả sử mặt phẳng (P), có cặp VTCP là \(\vec u_1\) và \(\vec u_2\) thì \(\vec{n}=\left [ \overrightarrow{u_1}; \overrightarrow{u_2} \right ]\) là một VTPT của mặt phẳng (P).
Lời giải:
Ta có lời giải chi tiết câu a, b bài 5 như sau:
Câu a:
Ta có \(\overrightarrow{AC}=(0;-1;1); \overrightarrow{AD}=(-1;-1;3)\)
Mặt phẳng (ACD) có vecto pháp tuyến \(\vec{n}=\left [ \overrightarrow{AC}, \overrightarrow{AD} \right ]= (-2;-1;-1)\)
Vậy phương trình của mặt phẳng (ACD) là:
\(-2(x-5)-1(y-1)-1(z-3)=0\Leftrightarrow 2x+y+z-14=0\)
Câu b:
Ta có: \(\overrightarrow{AB}=(-4;5;-1); \overrightarrow{CD}=(-1;0;2)\).
Suy ra mặt phẳng \((\alpha )\) đi qua AB và song song với CD nên có một vectơ pháp tuyến là \(\vec{n}=\left [ \overrightarrow{AB}, \overrightarrow{CD} \right ]=(10;9;5)\).
Vậy phương trình của mặt phẳng \((\alpha )\) là:
\(10(x-5)+9(y-1)+5(z-3)=0\Leftrightarrow 10x+9y+5z-74=0\).
-- Mod Toán 12 HỌC247
Video hướng dẫn giải bài 5 SGK
Bài tập SGK khác
Bài tập 3 trang 80 SGK Hình học 12
Bài tập 4 trang 80 SGK Hình học 12
Bài tập 6 trang 80 SGK Hình học 12
Bài tập 7 trang 80 SGK Hình học 12
Bài tập 8 trang 80 SGK Hình học 12
Bài tập 9 trang 81 SGK Hình học 12
Bài tập 10 trang 81 SGK Hình học 12
Bài tập 3.17 trang 103 SBT Hình học 12
Bài tập 3.18 trang 113 SBT Hình học 12
Bài tập 3.19 trang 113 SBT Hình học 12
Bài tập 3.20 trang 113 SBT Hình học 12
Bài tập 3.21 trang 113 SBT Hình học 12
Bài tập 3.22 trang 114 SBT Hình học 12
Bài tập 3.23 trang 114 SBT Hình học 12
Bài tập 3.24 trang 114 SBT Hình học 12
Bài tập 3.25 trang 114 SBT Hình học 12
Bài tập 3.26 trang 114 SBT Hình học 12
Bài tập 3.27 trang 114 SBT Hình học 12
Bài tập 3.28 trang 114 SBT Hình học 12
Bài tập 3.29 trang 114 SBT Hình học 12
Bài tập 3.30 trang 114 SBT Hình học 12
Bài tập 15 trang 89 SGK Hình học 12 NC
Bài tập 16 trang 89 SGK Hình học 12 NC
Bài tập 17 trang 89 SGK Hình học 12 NC
Bài tập 18 trang 90 SGK Hình học 12 NC
Bài tập 19 trang 90 SGK Hình học 12 NC
Bài tập 20 trang 90 SGK Hình học 12 NC
Bài tập 21 trang 90 SGK Hình học 12 NC
-


Hãy viết phương trình mặt phẳng đi qua điểm M0(1;3;-2) và vuông góc với đường thẳng BC với B=(0;2;-3), C=(1;-4;1).
bởi Phạm Hoàng Thị Trà Giang
 25/05/2021
25/05/2021
Hãy viết phương trình mặt phẳng đi qua điểm M0(1;3;-2) và vuông góc với đường thẳng BC với B=(0;2;-3), C=(1;-4;1).
Theo dõi (0) 1 Trả lời -


Hãy viết phương trình mặt phẳng đi qua điểm M0(1;3;-2) và vuông góc với trục Oy.
bởi Lê Minh Bảo Bảo
 25/05/2021
25/05/2021
Hãy viết phương trình mặt phẳng đi qua điểm M0(1;3;-2) và vuông góc với trục Oy.
Theo dõi (0) 1 Trả lời -


Hãy viết phương trình mặt phẳng đi qua ba điểm A(-1;2;3),B(2;-4;3), C(4;5;6).
bởi hà trang
 25/05/2021
25/05/2021
Hãy viết phương trình mặt phẳng đi qua ba điểm A(-1;2;3),B(2;-4;3), C(4;5;6).
Theo dõi (0) 1 Trả lời -


Cho điểm \({M_0}({x_0},{y_0},{z_0})\) với \({x_0},{y_0},{z_0} \ne 0.\) Đi qua điểm M0 và lần lượt chứa các trục tọa độ Ox, Oy, Oz.
bởi Thanh Thanh
 25/05/2021
25/05/2021
Cho điểm \({M_0}({x_0},{y_0},{z_0})\) với \({x_0},{y_0},{z_0} \ne 0.\) Đi qua điểm M0 và lần lượt chứa các trục tọa độ Ox, Oy, Oz.
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho điểm \({M_0}({x_0},{y_0},{z_0})\) với \({x_0},{y_0},{z_0} \ne 0.\) Đi qua các hình chiếu của điểm M0 trên các trục tọa độ Ox, Oy, Oz.
bởi Vương Anh Tú
 25/05/2021
25/05/2021
Cho điểm \({M_0}({x_0},{y_0},{z_0})\) với \({x_0},{y_0},{z_0} \ne 0.\) Đi qua các hình chiếu của điểm M0 trên các trục tọa độ Ox, Oy, Oz.
Theo dõi (0) 1 Trả lời -


Cho điểm \({M_0}({x_0},{y_0},{z_0})\) với \({x_0},{y_0},{z_0} \ne 0.\) Viết phương trình mặt phẳng đi qua diểm M0 và song song với một trong các mặt phẳng tọa độ (Oxy), (Oyz), (Oxz).
bởi Mai Trang
 25/05/2021
25/05/2021
Cho điểm \({M_0}({x_0},{y_0},{z_0})\) với \({x_0},{y_0},{z_0} \ne 0.\) Viết phương trình mặt phẳng đi qua diểm M0 và song song với một trong các mặt phẳng tọa độ (Oxy), (Oyz), (Oxz).
Theo dõi (0) 1 Trả lời -


Hãy lập phương trình của mặt phẳng \((\alpha )\) đi qua điểm M(1; 2; 3) và cắt ba tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất.
bởi Ngoc Son
 24/05/2021
24/05/2021
Hãy lập phương trình của mặt phẳng \((\alpha )\) đi qua điểm M(1; 2; 3) và cắt ba tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất.
Theo dõi (0) 1 Trả lời -


Hãy viết phương trình của mặt phẳng \((\beta )\) đi qua điểm M(2; -1; 2), song song với trục Oy và vuông góc với mặt phẳng \((\alpha )\): 2x – y + 3z + 4 = 0.
bởi can chu
 25/05/2021
25/05/2021
Hãy viết phương trình của mặt phẳng \((\beta )\) đi qua điểm M(2; -1; 2), song song với trục Oy và vuông góc với mặt phẳng \((\alpha )\): 2x – y + 3z + 4 = 0.
Theo dõi (0) 1 Trả lời -


Hãy xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình tổng quát sau đây: \(({\alpha _3}):x - y + 2z - 4 = 0,\)\(({\alpha _3}'):10x - 10y + 20z - 40 = 0\).
bởi Nguyễn Tiểu Ly
 24/05/2021
24/05/2021
Hãy xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình tổng quát sau đây: \(({\alpha _3}):x - y + 2z - 4 = 0,\)\(({\alpha _3}'):10x - 10y + 20z - 40 = 0\).
Theo dõi (0) 1 Trả lời


