Giải bài 3.19 tr 113 SBT Hình học 12
Cho tứ diện ABCD có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0 ; 4), D(4; 0 ; 6)
a) Hãy viết phương trình mặt phẳng (ABC).
b) Hãy viết phương trình mặt phẳng \((\alpha )\) đi qua điểm D và song song với mặt phẳng (ABC).
Hướng dẫn giải chi tiết
a) Ta có: \(\overrightarrow {AB} = ( - 4;5; - 1)\) và \(\overrightarrow {AC} = (0; - 1;1)\) suy ra \(\vec n = \overrightarrow {AB} \wedge \overrightarrow {AC} = (4;4;4)\)
Do đó (ABC) có vecto pháp tuyến là \(\vec n = (4;4;4)\) hoặc \({\vec n^\prime } = (1;1;1)\)
Suy ra phương trình của (ABC) là: (x – 5) + (y – 1) + (z – 3) = 0 hay x + y + z – 9 =0
b) Mặt phẳng \((\alpha )\) đi qua điểm D và song song với mặt phẳng (ABC) nên \((\alpha )\) cũng có vecto pháp tuyến là \({\vec n^\prime } = (1;1;1)\)
Vậy phương trình của \((\alpha )\) là: (x – 4) + (y) + (z – 6) = 0 hay x + y + z – 10 = 0.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.17 trang 103 SBT Hình học 12
Bài tập 3.18 trang 113 SBT Hình học 12
Bài tập 3.20 trang 113 SBT Hình học 12
Bài tập 3.21 trang 113 SBT Hình học 12
Bài tập 3.22 trang 114 SBT Hình học 12
Bài tập 3.23 trang 114 SBT Hình học 12
Bài tập 3.24 trang 114 SBT Hình học 12
Bài tập 3.25 trang 114 SBT Hình học 12
Bài tập 3.26 trang 114 SBT Hình học 12
Bài tập 3.27 trang 114 SBT Hình học 12
Bài tập 3.28 trang 114 SBT Hình học 12
Bài tập 3.29 trang 114 SBT Hình học 12
Bài tập 3.30 trang 114 SBT Hình học 12
Bài tập 15 trang 89 SGK Hình học 12 NC
Bài tập 16 trang 89 SGK Hình học 12 NC
Bài tập 17 trang 89 SGK Hình học 12 NC
Bài tập 18 trang 90 SGK Hình học 12 NC
Bài tập 19 trang 90 SGK Hình học 12 NC
Bài tập 20 trang 90 SGK Hình học 12 NC
Bài tập 21 trang 90 SGK Hình học 12 NC
-


Tìm VTPT của mặt phẳng (Q)?
bởi Ber
 11/05/2020
11/05/2020
Mn giúp mình câu 20 với với ạ
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Cho vectoAB=(2; -3;1) và A(1; -2; 4), tìm tọa độ B
bởi Thanh Tuyền
 10/05/2020
Hicc em cần cách gửi của mấy bài này ạ T.T
10/05/2020
Hicc em cần cách gửi của mấy bài này ạ T.T Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Cho ba mặt phẳng , (a) x 2y-z-6, (b) 2x-y 3z 13 , (y) 3x-2y 3z 16 đi qua điểm A tìm tọa độ điểm A?
bởi Nguyễn Hải
 07/05/2020
07/05/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Trong không gian Oxyz Cho tứ diện ABCD A(0,1,-1) B(1,1,2) C(1,-1,0) D(0,0,1). Viết phương trình tổng quát của mặt phẳng Q song song với mặt phẳng bcd và chia tứ diện thành 2 phần có tỉ số thể tích phần chứa điểm A và phần còn lại bằng một phần 1/26
bởi Tuyen Pham
 06/05/2020
Giúp mình vớiTheo dõi (0) 0 Trả lời
06/05/2020
Giúp mình vớiTheo dõi (0) 0 Trả lời -
ADMICRO


 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Trong không gian oxyz cho mặt cầu (s):(x-1)^2+(y-1)^2+(z-1)^2=9 pt mặt phẳng tiếp xúc với mặt cầu (s) tại điểm M(0;-1;3)
bởi nguyễn yến nhi
 04/05/2020
Theo dõi (0) 0 Trả lời
04/05/2020
Theo dõi (0) 0 Trả lời -


Tìm vectơ pháp tuyến của mặt phẳng?
bởi Nguyễn Thùy Tiên
 24/04/2020
24/04/2020
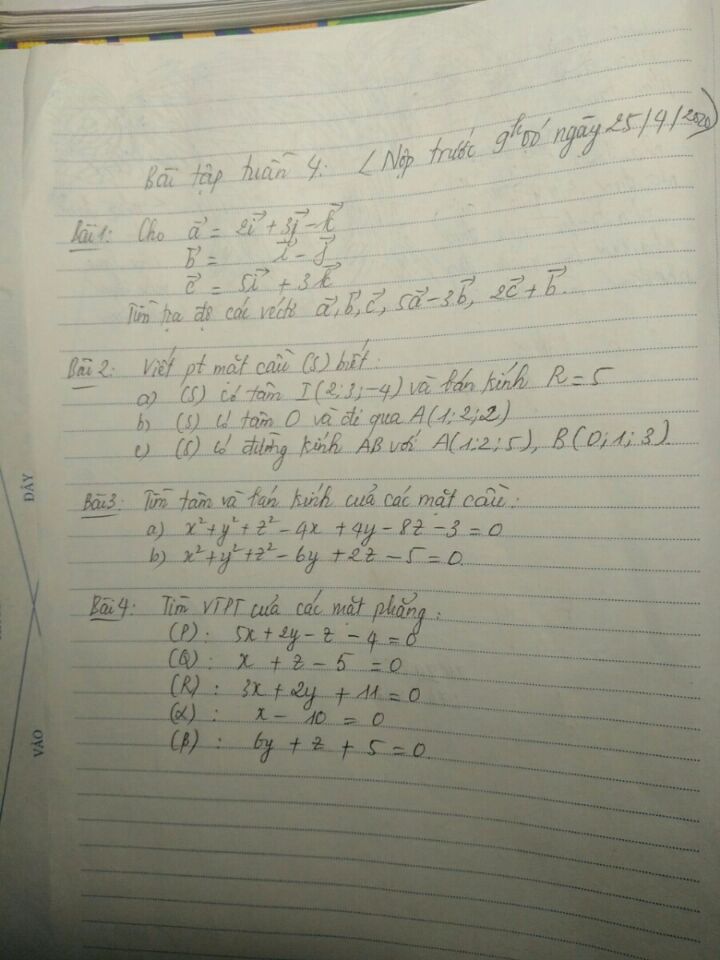 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Lm tự luận
Lm tự luận Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Viết phương trình đường thẳng (P) qua A vs vuông góc BC biết A(2,0,0), B(1,0,4), C(3,-2,0)
bởi Kim Thoa
 22/04/2020
22/04/2020
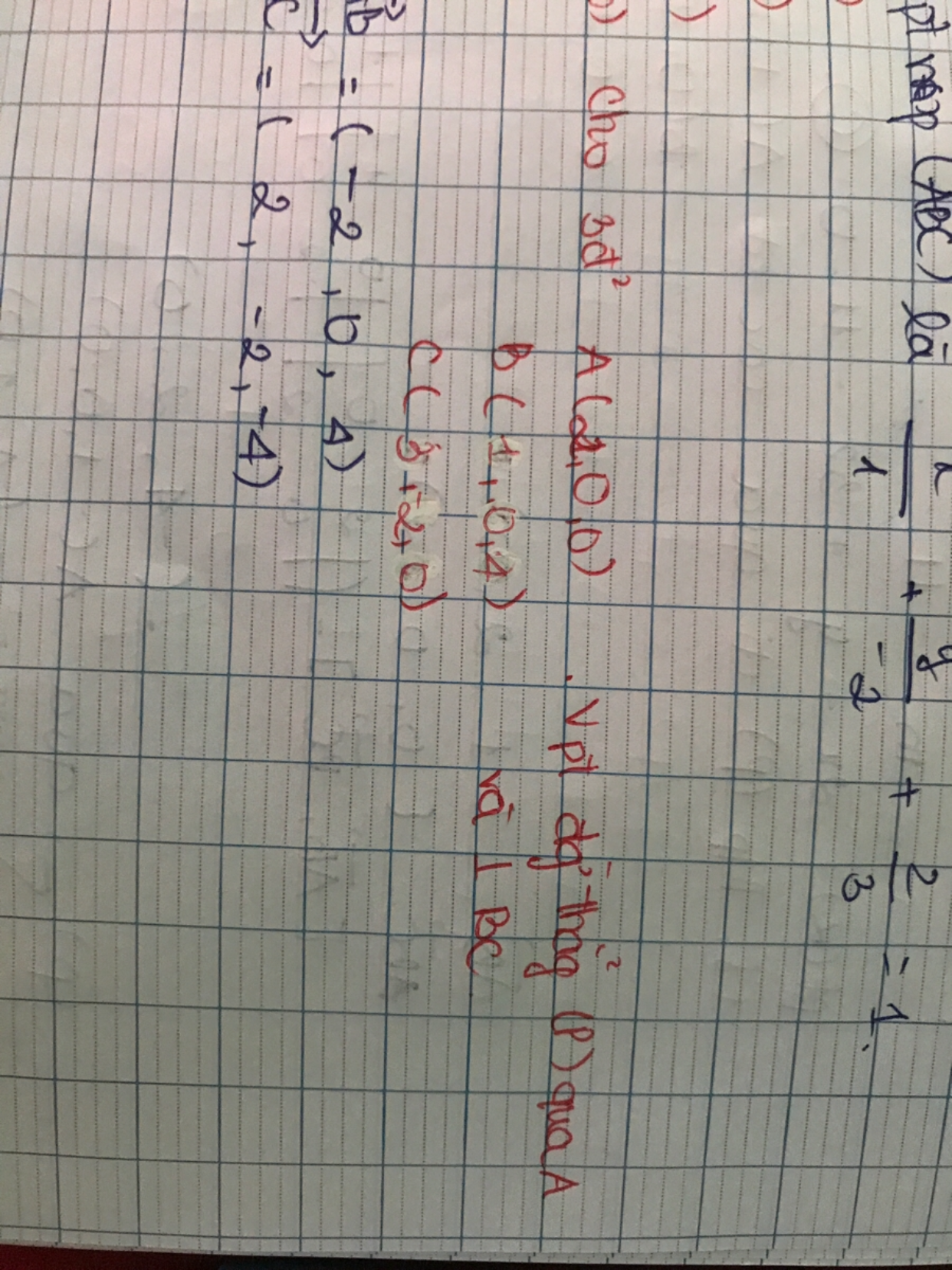 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời


