Bài tập 22 trang 90 SGK Hình học 12 NC
Cho tứ diện OABC có các tam giác OAB, OBC, OCA là những tam giác vuông đỉnh O. Gọi α, β, γ lần lượt là góc giữa mặt phẳng (ABC) và các mặt phẳng (OBC), (OCA), (OAB). Bằng phương pháp toạ độ, hãy chứng minh :
a) Tam giác ABC có ba góc nhọn.
b) \(co{s^2}\alpha + co{s^2}\beta + co{s^2}\gamma = 1\)
Hướng dẫn giải chi tiết
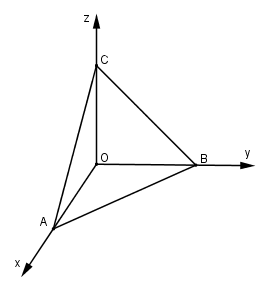
a) Chọn hệ trục tọa độ Oxyz như hình vẽ.
Ta có A(a; 0; 0), B(0; b; 0), C(0; 0; c) (a > 0, b > 0, c > 0) (a > 0, b > 0, c > 0)
Ta có
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB} = ( - a;b;0);\overrightarrow {AC} = ( - a;0;c)\\
\Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = {a^2} > 0
\end{array}\\
{ \Rightarrow cosA = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} > 0}
\end{array}\)
⇒ A là góc nhọn
Tương tự các góc B, C của tam giác ABC cũng nhọn.
b) Mp(ABC) có phương trình \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\)
Nên có vecto pháp tuyến \(\vec n = \left( {\frac{1}{a};\frac{1}{b};\frac{1}{c}} \right)\)
Mp(OBC) ≡ Mp(Oyz) có vectơ pháp tuyến \(\vec i = \left( {1;0;0} \right)\)
Gọi α là góc giữa mp(ABC) và mp(OBC) thì:
\({\cos ^2}\alpha = {\left( {\frac{{\overrightarrow n .\overrightarrow i }}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow i } \right|}}} \right)^2} = \frac{{\frac{1}{{{a^2}}}}}{{\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}}}\)
Tương tự
\(\begin{array}{l}
{\cos ^2}\beta = \frac{{\frac{1}{{{b^2}}}}}{{\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}}};\\
{\cos ^2}\gamma = \frac{{\frac{1}{{{c^2}}}}}{{\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}}}
\end{array}\)
Vậy \(co{s^2}\alpha + co{s^2}\beta + co{s^2}\gamma = 1\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
-


Viết phương trình mặt phẳng (\(\alpha\)) đi qua đỉnh D và song song với mặt phẳng (ABC)
bởi Thanh Truc
 08/02/2017
08/02/2017
Trong không gian với hệ tọa độ Oxyz, cho tứ diện có các đỉnh là A (5; 1; 3), B (1; 6; 2), C (6; 2; 4) và D (4; 0; 6).
1) Viết phương trình mặt phẳng (\(\alpha\)) đi qua đỉnh D và song song với mặt phẳng (ABC).
2) Tính thể tích tứ diện ABCD.
Theo dõi (0) 2 Trả lời -


Viết phương trình mặt phẳng (Q) đi qua M và song song với mặt phẳng (P)
bởi Nguyễn Hồng Tiến
 07/02/2017
07/02/2017
Trong không gian với hệ tọa độ Oxyz , cho điểm M (1; -2;0) và mặt phẳng (P): 2x - 2y +z - 2 = 0. Viết phương trình mặt phẳng (Q) đi qua M và song song với mặt phẳng (P) . Viết phương trình mặt cầu tâm M và tiếp xúc với mặt phẳng (P).
Theo dõi (0) 2 Trả lời -


Viết phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ C đến (P) bằng khoảng cách từ (D) đến (P)
bởi Thanh Nguyên
 07/02/2017
07/02/2017
Trong không gian hệ tọa độ Oxyz, cho tứ diện ABCD có các đỉnh A (1; 2; 1), B (-2; 1; 3), C (2; -1; 1) và D (0; 3; 1). Viết phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ C đến (P) bằng khoảng cách từ (D) đến (P).
Theo dõi (0) 2 Trả lời -


Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;1;1;), B(2;2;2), C(2;0;5), D(0;2;1). Viết phương trình mặt phẳng chứa A và B đi qua trung điểm của đoạn CD.
Theo dõi (0) 1 Trả lời -
ADMICRO


Viết phương trình mặt phẳng (ABC) và tìm tọa độ giao điểm của d với mặt phẳng (ABC)
bởi Lê Bảo An
 08/02/2017
08/02/2017
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-1;1;2), B(0;1;1), C(1;0;4) và đường thẳng \(d: \left\{\begin{matrix} x=-t\\ y=2+t\\ z=3-t \end{matrix}\right, t\in R\)
Viết phương trình mặt phẳng (ABC) và tìm tọa độ giao điểm của d với mặt phẳng (ABC).Theo dõi (0) 2 Trả lời -


Viết phương trình mặt phẳng trung trực đoạn AB và tìm điểm M trên mặt phẳng (P) sao cho MA = MB = 13
bởi Bo bo
 06/02/2017
06/02/2017
Trong không gian tọa độ Oxyz , cho hai điểm \(A (4;-2;11), B(-2;-10;3)\) và mặt phẳng \((P): x+y-z-4=0\). Viết phương trình mặt phẳng trung trực đoạn AB và tìm điểm M trên mặt phẳng (P) sao cho MA = MB = 13
Theo dõi (0) 1 Trả lời -


Viết phương trình mặt phẳng trung trực (P) của đoạn thẳng AB và phương trình mặt cầu tâm O, tiếp xúc với (P)
bởi thu trang
 08/02/2017
08/02/2017
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2; 0; 0) và B(1; 1; - 1). Viết phương trình mặt phẳng trung trực (P) của đoạn thẳng AB và phương trình mặt cầu tâm O, tiếp xúc với (P).
Theo dõi (0) 3 Trả lời



