ON
ON
YOMEDIA
12AMBIENT

Ôn tập Toán 12 Chương 4 Số Phức

Tuy là một khái niệm mới nhưng Số phức được xem là một trong những dạng toán dễ trong chương trình phổ thông. Tài liệu Ôn tập Toán 12 Chương 4 sau đây về Số phức sẽ giúp các em tổng hợp lại hệ thống kiến thức đã được học trong các bài, bên cạnh đó là những bài tập tổng hợp có hướng dẫn giải sẽ giúp các em rèn luyện kĩ năng làm bài và nắm vững kiến thức hơn. Tại đây, HỌC247 còn cung cấp thêm các đề kiểm tra 1 tiết Số phức được biên soạn theo hình thức trắc nghiệm online nhằm giúp các em có thể tự luyện tập cùng một số file đề thi có đầy đủ đáp án chi tiết được tổng hợp từ nhiều trường THPT khác nhau. Mời các em cùng tham khảo.

ANYMIND360-ADSENSE/

Đề cương Ôn tập Toán 12 Chương 4

A. Tóm tắt lý thuyết 

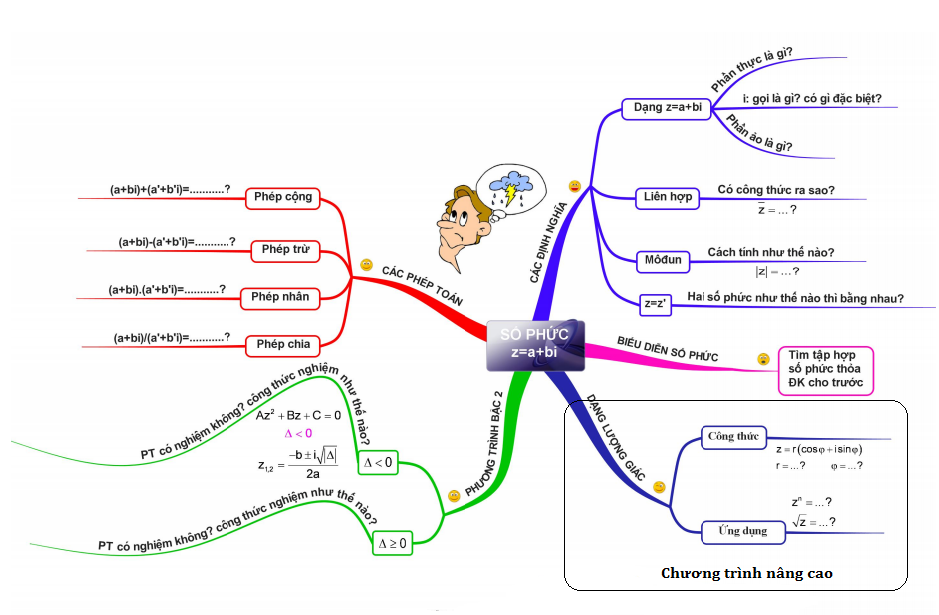
Hệ thống hóa số phức và các dạng toán liên quan

1. Số phức

  • Số phức \(z = a + bi\) có phần thực là \(a\), phần ảo là \(b\) (\(a,b\in\mathbb{R}\) và \(i^2=-1\)).
  • Số phức bằng nhau: \(a + bi = c + di \Leftrightarrow \left\{ \begin{array}{l}
    a = c\\
    b = d
    \end{array} \right.\)
  • Số phức \(z = a + bi\) được biểu diễn bới điểm \(M(a,b)\) trên mặt phẳng toạ độ.

  • Môđun của số phức \(z\) là \(\left| z \right| = \left| {\overrightarrow {OM} } \right| = \sqrt {{a^2} + {b^2}} \)

  • Số phức liên hợp của số phức \(z = a + bi\) là \(a-bi\) kí hiệu là \(\overline z = a - bi.\)

​                               

  • Đặc biệt: 
    • \(a = 0 \to z = bi\): Số ảo (Số thuần ảo)
    • \(b = 0 \to z = a\): Số thực
    • \(z = 0\): Vừa là số thực, vừa là số ảo

2. Công thức cộng, trừ và nhân hai số phức

Cho hai số phức \({z_1} = a + bi,\,\,{z_2} = c + di\,(a,b,c,d \in \mathbb{R}),\) ta có:

  • \(z_1+z_2=(a + bi) + ( c + di) = (a + c) + (b + d)i\)
  • \(z_1-z_2=(a + bi) - ( c + di) = (a - c) + (b - d)i\)
  • \(z_1.z_2=(a + bi)( c + di) = (ac - bd) + (ad + bc)i\)

3. Phép chia hai số phức 

Cho hai số phức \({z_1} = a + bi,\,\,{z_2} = c + di\,(a,b,c,d \in \mathbb{R}),\) ta có:

\(\frac{{c + di}}{{a + bi}} = \frac{{\left( {c + di} \right)(a - bi)}}{{{a^2} + {b^2}}} = \frac{{ac + bd}}{{{a^2} + {b^2}}} + \frac{{ad - bc}}{{{a^2} + {b^2}}}i\)

(Nhân cả tử và mẫu với \(a - bi\) (số phức liên hợp của mẫu)).

4. Phương trình bậc hai với hệ số phức

  • Các căn bậc hai của số thực \(a<0\) là \(\pm i\sqrt a.\)
  • Xét phương trình bậc hai \(ax^2 + bx + c = 0\) với \(a,b,c\in \mathbb{R},a\ne0.\)

Đặt \(\Delta=b^2-4ac\):

  • Nếu \(\Delta=0\) thì phương trình có một nghiệm kép (thực) \(x=-\frac{b}{2a}.\)
  • Nếu \(\Delta>0\) thì phương trình có hai nghiệm thực \(x_{1,2}=\frac{-b\pm \sqrt \Delta}{2a}.\)
  • Nếu \(\Delta<0\) thì phương trình có hai nghiệm phức \({x_{1,2}} = \frac{{ - b \pm i\sqrt {\left| \Delta \right|} }}{{2a}}.\)

B. Bài tập minh họa

Bài 1: Tìm số phức z sao cho (1 +2i)z là số thuần ảo và \(\left | 2.z-\bar{z} \right |=\sqrt{13}\).

Hướng dẫn giải

Giả sử \(z=a+bi \ (a,b\in R)\).

Khi đó \((1+2i)z=(1+2i)(a+bi)=(a-2b)+(2a+b)i.\)

(1 + 2i)z là số thuần ảo khi và chỉ khi: \(a-2b=0\Leftrightarrow a=2b\)

\(\left | 2.z-\bar{z} \right |=\left | a+3bi \right |=\left | 2b+3bi \right | =\sqrt{13b^2}=\sqrt{13}\Leftrightarrow b=\pm 1.\)

Vậy có hai số phức thỏa mãn đề bài: \(z=2+i;z=-2-i.\)

Bài 2: Tìm phần thực và phần ảo của số phức z thoả mãn điều kiện \(z+(2+i)\bar{z}=3+5i.\)

Hướng dẫn giải

Giả sử \(z=a+bi(a,b\in R)\)
Ta có 
\(z+(1+i)\bar{z}=3+5i\Leftrightarrow a+bi+(2+i)(a-bi)=3+5i\)
\(\Leftrightarrow 3a+b+(a-b)i=3+5i\)
\(\Leftrightarrow \left\{\begin{matrix} 3a+b=3\\ a-b=5 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=2\\ b=-3 \end{matrix}\right.\)
Vậy z = 2 - 3i.

Do đó phần thực của z là 2 và phần ảo của z là –3.

Bài 3: Cho hai số phức \(z_1,z_2\) thỏa mãn \(\left |z_1 \right |=\left |z_2 \right |=1,\left |z_1 +z_2 \right | =\sqrt{3}\). Tính \(\left |z_1 -z_2 \right |.\)

Hướng dẫn giải

Đặt: \(z_1=a_1+b_1i;z_2=a_2+b_2i \ (a_1,a_2,b_1,b_2 \in R)\)
\(\left\{\begin{matrix} \left | z_1 \right | =\left | z_2 \right |=1\\ \left | z_1 +z_2\right |=\sqrt{3} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} a^2_1+b^2_1=a^2_2+b^2_2=1\\ (a_1+b_2)^2+(b_1+b_2)^2=2 \end{matrix}\right.\)
\(\Leftrightarrow 2(a_1b_1+a_2b_2)=1\Rightarrow (a_1-a_2)^2+(b_1-b_2)^2=1\)
Vậy \(\left | z_1-z_2 \right |=1.\)

Bài 4: Cho số phức z thỏa mãn điều kiện \((1+2i)z+(3+2i)\bar{z}=4+10i.\) Tìm môđun của số phức \(w=z+2\bar{z}.\)

Hướng dẫn giải

Đặt \(z=a+bi(a,b\in R)\Rightarrow \bar{z}=a-bi\)
Ta có \((1+2i)z+(3+2i)\bar{z}=4+10i\)
\(\Leftrightarrow (1+2i)(a+bi)+(3+2i)(a-bi)(a-bi)=4+10i\)
\(\Leftrightarrow 4a+(4a-2b)i=4+10i\Leftrightarrow \left\{\begin{matrix} 4a=4\\ 4a-2b=10 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=1\\ b=-3 \end{matrix}\right.\)
Do đó \(z= 1- 3i.\)
Ta có: \(w=z+2\bar{z}=1-3i+2(1+3i)=3+3i.\)
Suy ra môđun của w là \(\left | w \right |=\sqrt{3^2+3^2}=3\sqrt{2}.\)

Trắc nghiệm Toán 12 Chương 4

Đề kiểm tra Toán 12 Chương 4

Đề kiểm tra trắc nghiệm online Chương 4 Toán 12 (Thi Online)

Phần này các em được làm trắc nghiệm online trong vòng 45 phút để kiểm tra năng lực và sau đó đối chiếu kết quả và xem đáp án chi tiết từng câu hỏi.

Đề kiểm tra Chương 4 Toán 12 (Tải File)

Phần này các em có thể xem online hoặc tải file đề thi về tham khảo gồm đầy đủ câu hỏi và đáp án làm bài.

Lý thuyết từng bài Chương 4 và hướng dẫn giải bài tập SGK

Lý thuyết các bài học Toán 12 Chương 4

Hướng dẫn giải bài tập Toán 12 Chương 4

Để xem nội dung đầy đủ, chi tiết, các em đăng nhập vào tài khoản trên trang Hoc247.net. Trên mỗi tài liệu, Hoc247 đều hỗ trợ chức năng chia sẻ lên Facebook để giới thiệu bạn bè cùng vào học, tích lũy thêm điểm HP và có cơ hội nhận thêm nhiều phần quà có giá trị từ HỌC247! Chúc các em đạt kết quả thật cao.    

OFF

XEM NHANH CHƯƠNG TRÌNH LỚP 12

ON