Giải bài 3.17 tr 103 SBT Hình học 12
Viết phương trình mặt phẳng \((\alpha )\) trong các trường hợp sau:
a) \((\alpha )\) đi qua điểm M(2;0; 1) và nhận \(\vec n = (1;1;1)\) làm vecto pháp tuyến ;
b) \((\alpha )\) đi qua điểm A(1; 0; 0) và song song với giá của hai vecto \(\vec u = (0;1;1),\vec v = ( - 1;0;2)\) ;
c) \((\alpha )\) đi qua ba điểm M(1;1;1), N(4; 3; 2), P(5; 2; 1).
Hướng dẫn giải chi tiết
a) Phương trình \((\alpha )\) có dạng: (x – 2)+ (y) + (z – 1) = 0 hay x + y + z – 3 = 0
b) Hai vecto có giá song song với mặt phẳng \((\alpha )\) là: \(\vec u = (0;1;1)\) và \(\vec v = ( - 1;0;2)\).
Suy ra \((\alpha )\) có vecto pháp tuyến là \(\vec n = \vec u \wedge \vec v = (2; - 1;1)\)
Mặt phẳng \((\alpha )\) đi qua điểm A(1; 0; 0) và nhận \(\vec n = (2; - 1;1)\) là vecto pháp tuyến. Vậy phương trình của \((\alpha )\) là: 2(x – 1) – y +z = 0 hay 2x – y + z – 2 = 0
c) Hai vecto có giá song song hoặc nằm trên \((\alpha )\) là: \(\overrightarrow {MN} = (3;2;1)\) và \(\overrightarrow {MP} = (4;1;0)\).
Suy ra \((\alpha )\) có vecto pháp tuyến là \(\vec n = \overrightarrow {MN} \wedge \overrightarrow {MP} = ( - 1;4; - 5)\)
Vậy phương trình của \((\alpha )\) là: -1(x – 1) + 4(y – 1) – 5(z – 1) = 0 hay x – 4y + 5z – 2 = 0.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 9 trang 81 SGK Hình học 12
Bài tập 10 trang 81 SGK Hình học 12
Bài tập 3.18 trang 113 SBT Hình học 12
Bài tập 3.19 trang 113 SBT Hình học 12
Bài tập 3.20 trang 113 SBT Hình học 12
Bài tập 3.21 trang 113 SBT Hình học 12
Bài tập 3.22 trang 114 SBT Hình học 12
Bài tập 3.23 trang 114 SBT Hình học 12
Bài tập 3.24 trang 114 SBT Hình học 12
Bài tập 3.25 trang 114 SBT Hình học 12
Bài tập 3.26 trang 114 SBT Hình học 12
Bài tập 3.27 trang 114 SBT Hình học 12
Bài tập 3.28 trang 114 SBT Hình học 12
Bài tập 3.29 trang 114 SBT Hình học 12
Bài tập 3.30 trang 114 SBT Hình học 12
Bài tập 15 trang 89 SGK Hình học 12 NC
Bài tập 16 trang 89 SGK Hình học 12 NC
Bài tập 17 trang 89 SGK Hình học 12 NC
Bài tập 18 trang 90 SGK Hình học 12 NC
Bài tập 19 trang 90 SGK Hình học 12 NC
Bài tập 20 trang 90 SGK Hình học 12 NC
Bài tập 21 trang 90 SGK Hình học 12 NC
-


Viết phương trình mặt phẳng (P), biết mặt phẳng (P) đi qua M(2;1;5) và (P) song song với AB và CD. Biết A(3;0;1) ; B(0;-1;4); C(2;-2;1); D(1;1;1).
bởi Thuỳ Trang
 20/02/2021
Viết phương trình mặt phẳng (P), biết mặt phẳng (P) đi qua M(2;1;5) và (P) song song với AB và CD. Biết A(3;0;1) ; B(0;-1;4); C(2;-2;1); D(1;1;1)Theo dõi (0) 0 Trả lời
20/02/2021
Viết phương trình mặt phẳng (P), biết mặt phẳng (P) đi qua M(2;1;5) và (P) song song với AB và CD. Biết A(3;0;1) ; B(0;-1;4); C(2;-2;1); D(1;1;1)Theo dõi (0) 0 Trả lời -


Ba mặt phẳng sau (p) 2x-y 3z-5=0 (Q)x y 2z 9=0 (R)x 2y-3z 22=0 có điểm A chung có toạ độ là
bởi Trân Trần
 29/01/2021
Ơn kiểm tra giữa kìTheo dõi (0) 0 Trả lời
29/01/2021
Ơn kiểm tra giữa kìTheo dõi (0) 0 Trả lời -


Tổng a+b+c?
bởi Phan Phương Thảo
 29/07/2020
29/07/2020
Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(-1;1;0) , B(1;1;-1) , C(0;-3;-2). Biết rằng phương trình mặt phẳng (ABC) có dạng ax+by+cz+7=0. Tổng a+b+c bằng.
Theo dõi (0) 4 Trả lời -


Công thức tổng quát của cấp số cộng là?
bởi Têrêxa Hồ Trí
 23/07/2020
Cấp số nhân và cộng
23/07/2020
Cấp số nhân và cộng Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Tìm giao điểm của d và (P)?
bởi nguyễn hữu trung
 11/07/2020
11/07/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Diện tích hình phẳng giới hạn bởi đồ thị hàm số y bằng x cộng 1 trên x trừ 2 và các trục tọa độ bằng?
bởi Duy Nguyễn
 10/07/2020
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y bằng x cộng 1 trên x trừ 2 và các trục tọa độ bằngTheo dõi (0) 0 Trả lời
10/07/2020
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y bằng x cộng 1 trên x trừ 2 và các trục tọa độ bằngTheo dõi (0) 0 Trả lời -


Trong không gian Oxyz, phương trình mặt câu (S) có tâm I(-2;3;4) và cắt mặt phẳng tọa độ (Oxz) theo một hình tròn giao tuyến có diện tích bằng \(16\pi\) có phương trình là?
bởi Thu Hảo
 12/06/2020
12/06/2020
Câu 33
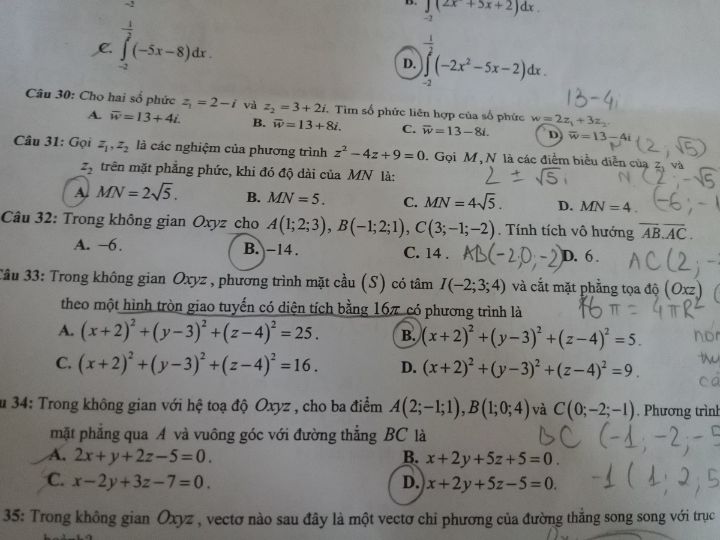 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Trong không gian Oxyz, phương trình mặt phẳng đi qua 2 điểm A(0;1;0) , B(2;0;1) và vuông góc với mặt phẳng (P) :x-y-z -1 =0 là?
bởi Thu Quỳnh
 10/06/2020
10/06/2020
Trong không gian OXYZ, phương trình mặt phẳng đi qua 2 điểm A(0;1;0) ,B(2;0;1) và vuông góc với mặt phẳng (P) :x-y-z -1 =0 là
Theo dõi (1) 4 Trả lời -


Trong không gian Oxyz, cho hai điểm A(1;3;0) và B(4;1;-2). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là?
bởi Thảo Nguyễn Thanh
 10/06/2020
10/06/2020
Trong không gian Oxyz, cho hai điểm A(1;3;0) và B(4;1;-2). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là:
Theo dõi (0) 6 Trả lời



