Giải bài 3.21 tr 113 SBT Hình học 12
Lập phương trình mặt phẳng \((\alpha )\) đi qua hai điểm A(0; 1; 0) , B(2; 3; 1) và vuông góc với mặt phẳng \((\beta )\) : x + 2y – z = 0 .
Hướng dẫn giải chi tiết
Mặt phẳng \((\alpha )\) đi qua hai điểm A, B và vuông góc với mặt phẳng \((\beta )\):
x + 2y – z = 0.
Vậy hai vecto có giá song song hoặc nằm trên \((\alpha )\) là \(\overrightarrow {AB} = (2;2;1)\) và \(\overrightarrow {{n_\beta }} = (1;2; - 1)\)
Suy ra \((\alpha )\) có vecto pháp tuyến là: \(\overrightarrow {{n_\alpha }} = ( - 4;3;2)\)
Vậy phương trình của \((\alpha )\) là: -4(x) + 3(y – 1) + 2z = 0 hay 4x – 3y – 2z + 3 = 0
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.19 trang 113 SBT Hình học 12
Bài tập 3.20 trang 113 SBT Hình học 12
Bài tập 3.22 trang 114 SBT Hình học 12
Bài tập 3.23 trang 114 SBT Hình học 12
Bài tập 3.24 trang 114 SBT Hình học 12
Bài tập 3.25 trang 114 SBT Hình học 12
Bài tập 3.26 trang 114 SBT Hình học 12
Bài tập 3.27 trang 114 SBT Hình học 12
Bài tập 3.28 trang 114 SBT Hình học 12
Bài tập 3.29 trang 114 SBT Hình học 12
Bài tập 3.30 trang 114 SBT Hình học 12
Bài tập 15 trang 89 SGK Hình học 12 NC
Bài tập 16 trang 89 SGK Hình học 12 NC
Bài tập 17 trang 89 SGK Hình học 12 NC
Bài tập 18 trang 90 SGK Hình học 12 NC
Bài tập 19 trang 90 SGK Hình học 12 NC
Bài tập 20 trang 90 SGK Hình học 12 NC
Bài tập 21 trang 90 SGK Hình học 12 NC
-


Phương trình mặt phẳng (P) qua A(2;1;4) và song song với giá của các vectơ a (1;2;0), b (−1;1;2)
bởi Anh Phuong
 15/04/2020
15/04/2020
Phương trình mặt phẳng (P) qua A(2;1;4) và song song với giá của các vectơ a⃗ (1;2;0),b⃗ (−1;1;2) là
Theo dõi (0) 2 Trả lời -


Viết phương trình mp(P)//(Q) và cắt (S) theo giao tuyến là một đường tròn có R=4
bởi Trâm Tina
 13/04/2020
13/04/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Đường thẳng d song song với mặt phẳng nào dưới đây?
bởi Rùa Rùa
 11/04/2020
11/04/2020
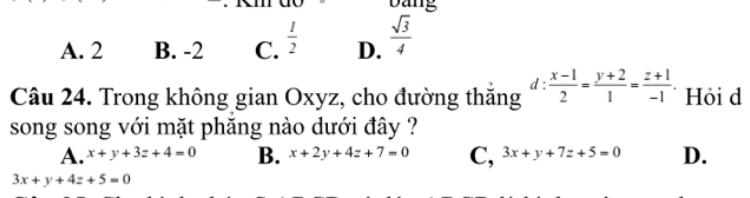 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Viết phương trình mp(Q) đi qua 2 điểm A(0;2;1) và B(-1;3:-2) và tạo mp (P) 2x-2y-2z 2=0 1 góc 45độ
bởi Ng Đức Hùng
 08/04/2020
Viết phương trình mp(Q) đi qua 2 điểm A(0;2;1) và B(-1;3:-2) và tạo mp (P) 2x-2y-2z 2=0 1 góc 45•Theo dõi (1) 3 Trả lời
08/04/2020
Viết phương trình mp(Q) đi qua 2 điểm A(0;2;1) và B(-1;3:-2) và tạo mp (P) 2x-2y-2z 2=0 1 góc 45•Theo dõi (1) 3 Trả lời -
ADMICRO


Viết phương trình mặt phẳng anpha đi qua điểm A và vuông góc với đường thẳng BC
bởi phamminhtu
 08/04/2020
Giúp em
08/04/2020
Giúp em Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -

 Giúp em
Giúp em Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -

 Giúp em
Giúp em Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Phương trình tổng quát của mặt phẳng (P) là?
bởi phamminhtu
 08/04/2020
08/04/2020
Giúp em
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời


