Giải bài 10 tr 81 sách GK Toán Hình lớp 12
Giải các bài toán sau đây bằng phương pháp tọa độ. Cho hình lập phương ABCD.A'B'C'D' cạnh bằng 1.
a) Chứng minh rằng hai mặt phẳng (AB'D') và (BC'D) song song với nhau.
b) Tính khoảng cách giữa hai mặt phẳng nói trên.
Hướng dẫn giải chi tiết bài 10
Phương pháp:
Từ dữ kiện đề bài, ta chọn một đỉnh bất kì của hình lập phương là gốc tọa độ. Khi đó, 3 cạnh của hình lập phương đi qua đỉnh đó chính là phương của các trục Ox, Oy, Oz.
Sau khi xây dựng xong hệ trục tọa độ, ta xác định tọa độ các đỉnh lúc này và tiến hành giải bài toán bằng phương pháp tọa độ trong không gian.
Giải sử, mặt phẳng (P) song song mặt phẳng (Q) thì khoảng cách từ (P) đến (Q) bằng khoảng cách từ một điểm bất kì thuộc (P) đến mặt phẳng (Q).
Lời giải:
Ta có lời giải chi tiết bài 10 như sau:
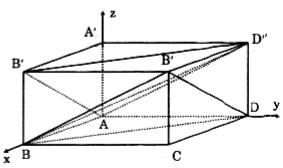
Xây dựng hệ trục tọa độ Oxyz như hình vẽ ta có tọa độ các đỉnh của hình lập phương là:
A(0;0;0), B(1;0;0), D(0;1;0), A'(0;0;1).
A'(0;0;1), B'(1;0;1), C'(1;1;1), D'(0;1;1).
Câu a:
Đặt \((\alpha )=(A'B'D')\) và \((\beta )=(BCD)\).
Ta có: \(\overrightarrow{AB'}=(1;0;1); \overrightarrow{AD'}=(0;1;1)\)
Suy ra mặt phẳng \((\alpha )\) có vecto pháp tuyến là \(\vec{n}=\left [ \overrightarrow{AB'},\overrightarrow{AD'} \right ]=(1;1;-1)\)
Vậy phương trình của mặt phẳng \((\alpha )\) là \(x+y-z=0\).
Ta có \(\overrightarrow{BC'}=(0;1;1)\)và \(\overrightarrow{BD}=(-1;1;0)\)
Suy ra mặt phẳng \((\beta )\) có vecto pháp tuyến là \(\vec{n}=\left [ \overrightarrow{BC'}, \overrightarrow{BD} \right ]=(-1;-1;1)\)
Phương trình mp \((\beta )\) là:
\(-1(x-1) -1.y+1.z=0\Leftrightarrow x+y-z-1=0\).
Ta có:
\(\frac{1}{1}=\frac{1}{1}=\frac{-1}{-1}\neq \frac{0}{-1}\), vậy hai mặt phẳng \((\alpha )\) và \((\beta )\) song song nhau.
Câu b:
Do mặt phẳng \((\alpha )\) và \((\beta )\) song song nhau nên:
\(d((\alpha ),(\beta ))=d(A,(\beta ))=\frac{\left | -1 \right |}{\sqrt{1^2+1^2+(-1)^2}}= \frac{1}{\sqrt{3}}\)
-- Mod Toán 12 HỌC247
Video hướng dẫn giải bài 10 SGK
Bài tập SGK khác
Bài tập 8 trang 80 SGK Hình học 12
Bài tập 9 trang 81 SGK Hình học 12
Bài tập 3.17 trang 103 SBT Hình học 12
Bài tập 3.18 trang 113 SBT Hình học 12
Bài tập 3.19 trang 113 SBT Hình học 12
Bài tập 3.20 trang 113 SBT Hình học 12
Bài tập 3.21 trang 113 SBT Hình học 12
Bài tập 3.22 trang 114 SBT Hình học 12
Bài tập 3.23 trang 114 SBT Hình học 12
Bài tập 3.24 trang 114 SBT Hình học 12
Bài tập 3.25 trang 114 SBT Hình học 12
Bài tập 3.26 trang 114 SBT Hình học 12
Bài tập 3.27 trang 114 SBT Hình học 12
Bài tập 3.28 trang 114 SBT Hình học 12
Bài tập 3.29 trang 114 SBT Hình học 12
Bài tập 3.30 trang 114 SBT Hình học 12
Bài tập 15 trang 89 SGK Hình học 12 NC
Bài tập 16 trang 89 SGK Hình học 12 NC
Bài tập 17 trang 89 SGK Hình học 12 NC
Bài tập 18 trang 90 SGK Hình học 12 NC
Bài tập 19 trang 90 SGK Hình học 12 NC
Bài tập 20 trang 90 SGK Hình học 12 NC
Bài tập 21 trang 90 SGK Hình học 12 NC
-


Hai mặt phẳng \((α)\) và \((β)\) có phương trình \((α): x - 2y + 3z + 1 = 0\); \((β): 2x – 4y + 6z + 1 = 0\). Có nhận xét gì về vecto pháp tuyến của chúng?
bởi bala bala
 06/05/2021
06/05/2021
Hai mặt phẳng \((α)\) và \((β)\) có phương trình \((α): x - 2y + 3z + 1 = 0\); \((β): 2x – 4y + 6z + 1 = 0\). Có nhận xét gì về vecto pháp tuyến của chúng?
Theo dõi (0) 1 Trả lời -


Tìm một vecto pháp tuyến của mặt phẳng \((α): 4x – 2y - 6z +7 = 0\).
Theo dõi (0) 1 Trả lời -


Hãy lập phương trình tổng quát của mặt phẳng \((MNP)\) với \(M(1; 1; 1), N(4; 3; 2), P(5; 2; 1)\).
bởi Nguyen Ngoc
 06/05/2021
06/05/2021
Hãy lập phương trình tổng quát của mặt phẳng \((MNP)\) với \(M(1; 1; 1), N(4; 3; 2), P(5; 2; 1)\).
Theo dõi (0) 1 Trả lời -


Trong không gian \(Oxyz\) cho ba điểm \(A(2; -1; 3), B(4; 0; 1), C(-10; 5; 3)\). Tìm tọa độ một vecto pháp tuyến của mặt phẳng \((ABC)\).
bởi Nguyễn Ngọc Sơn
 07/05/2021
07/05/2021
Trong không gian \(Oxyz\) cho ba điểm \(A(2; -1; 3), B(4; 0; 1), C(-10; 5; 3)\). Tìm tọa độ một vecto pháp tuyến của mặt phẳng \((ABC)\).
Theo dõi (0) 1 Trả lời -
ADMICRO


Trong mặt phẳng Oxyz , mặt cầu tâm O , qua M (0,0,2) viết phương trình
bởi Pham Nguyen Truc Vy
 02/05/2021
trong mặt phẳng oxyz , mặt cầu tâm O , qua M (0,0,2) viết phương trìnhTheo dõi (0) 0 Trả lời
02/05/2021
trong mặt phẳng oxyz , mặt cầu tâm O , qua M (0,0,2) viết phương trìnhTheo dõi (0) 0 Trả lời -


Trong không gian Oxyz, cho mặt phẳng (P):2x−y+2z+1=0 và hai điểm A(1;0; - 2), B(- 1;- 1;3). Mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phương trình là
bởi Hoàng Ngọc Dương
 30/03/2021
30/03/2021
Trong không gian Oxyz, cho mặt phẳng (P):2x−y+2z+1=0(P):2x−y+2z+1=0 và hai điểm A(1;0; - 2), B(- 1;- 1;3). Mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phương trình là
Theo dõi (0) 2 Trả lời -

 Giải đề
Giải đề Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Trong không với hệ tọa độ Oxyz cho ba điểm A B C tính bán kính mặt cầu ngoại tiếp tứ giác OABC.
bởi Tân Minh Nguyễn
 02/03/2021
trong không với hệ tọa độ oxyz cho ba điểm A B C tính bán kính mặt cầu ngoại tiếp tứ giác OABCTheo dõi (1) 2 Trả lời
02/03/2021
trong không với hệ tọa độ oxyz cho ba điểm A B C tính bán kính mặt cầu ngoại tiếp tứ giác OABCTheo dõi (1) 2 Trả lời -


Trong không gian oxyz cho tam giác ABC có A (-1;3;2) B (2;0;5) năm C (0;-2;1) phương trình đường trung tuyến AM của tam giác ABC là
bởi nông Đức Huy
 21/02/2021
21/02/2021
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời




