Giải bài 1.49 tr 43 SBT Hình học 10
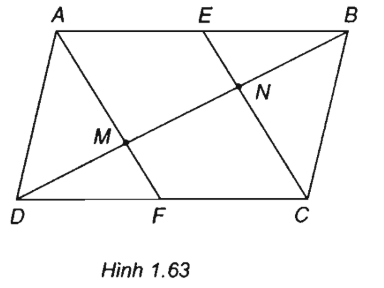
Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của hai cạnh AB và CD. Nối AF và CE, hai đường thẳng này cắt đường chéo BD lần lượt tại M và N. Chứng minh \(\overrightarrow {DM} = \overrightarrow {MN} = \overrightarrow {NB} \).
Hướng dẫn giải chi tiết
CF là hình bình hành //AM
là trung điểm của ⇒ là trung điểm của , do đó = NB.
Tương tự, M là trung điểm của , do đó = MN.
Vậy \(\overrightarrow {DM} = \overrightarrow {MN} = \overrightarrow {NB} \)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 13 trang 28 SGK Hình học 10
Bài tập 1.48 trang 43 SBT Hình học 10
Bài tập 1.50 trang 43 SBT Hình học 10
Bài tập 1.51 trang 43 SBT Hình học 10
Bài tập 1.52 trang 43 SBT Hình học 10
Bài tập 1.53 trang 43 SBT Hình học 10
Bài tập 1.54 trang 43 SBT Hình học 10
Bài tập 1.55 trang 43 SBT Hình học 10
Bài tập 1.56 trang 43 SBT Hình học 10
Bài tập 1.57 trang 44 SBT Hình học 10
Bài tập 1.58 trang 44 SBT Hình học 10
Bài tập 1.59 trang 44 SBT Hình học 10
Bài tập 1.60 trang 44 SBT Hình học 10
Bài tập 1.61 trang 44 SBT Hình học 10
Bài tập 1.62 trang 44 SBT Hình học 10
Bài tập 1.63 trang 44 SBT Hình học 10
Bài tập 1.64 trang 45 SBT Hình học 10
Bài tập 1.65 trang 45 SBT Hình học 10
Bài tập 1.66 trang 45 SBT Hình học 10
Bài tập 1.67 trang 45 SBT Hình học 10
Bài tập 1.68 trang 45 SBT Hình học 10
Bài tập 1.69 trang 45 SBT Hình học 10
Bài tập 1.70 trang 45 SBT Hình học 10
Bài tập 1.71 trang 46 SBT Hình học 10
Bài tập 1.72 trang 46 SBT Hình học 10
Bài tập 1.73 trang 46 SBT Hình học 10
Bài tập 1.74 trang 46 SBT Hình học 10
Bài tập 1.75 trang 46 SBT Hình học 10
Bài tập 1.76 trang 46 SBT Hình học 10
Bài tập 1.77 trang 46 SBT Hình học 10
Bài tập 1.78 trang 46 SBT Hình học 10
Bài tập 1.79 trang 47 SBT Hình học 10
Bài tập 1.80 trang 47 SBT Hình học 10
Bài tập 1.81 trang 47 SBT Hình học 10
Bài tập 1.82 trang 47 SBT Hình học 10
Bài tập 1.83 trang 47 SBT Hình học 10
Bài tập 1.84 trang 48 SBT Hình học 10
Bài tập 1.85 trang 47 SBT Hình học 10
Bài tập 1.86 trang 48 SBT Hình học 10
Bài tập 1.87 trang 48 SBT Hình học 10
Bài tập 1.88 trang 48 SBT Hình học 10
Bài tập 1.89 trang 49 SBT Hình học 10
Bài tập 1.90 trang 49 SBT Hình học 10
Bài tập 1.91 trang 49 SBT Hình học 10
Bài tập 1.92 trang 49 SBT Hình học 10
Bài tập 1.93 trang 49 SBT Hình học 10
Bài tập 1.95 trang 49 SBT Hình học 10
Bài tập 1.96 trang 49 SBT Hình học 10
Bài tập 1.97 trang 50 SBT Hình học 10
Bài tập 1.98 trang 50 SBT Hình học 10
Bài tập 1.99 trang 50 SBT Hình học 10
Bài tập 1.100 trang 50 SBT Hình học 10
Bài tập 1 trang 34 SGK Hình học 10 NC
Bài tập 2 trang 34 SGK Hình học 10 NC
Bài tập 3 trang 34 SGK Hình học 10 NC
Bài tập 4 trang 34 SGK Hình học 12 NC
Bài tập 5 trang 35 SGK Hình học 12 NC
Bài tập 6 trang 35 SGK Hình học 12 NC
Bài tập 7 trang 36 SGK Hình học 10 NC
Bài tập 8 trang 36 SGK Hình học10 NC
Bài tập 9 trang 36 SGK Hình học 10 NC
Bài tập 10 trang 36 SGK Hình học 10 NC
Bài tập 11 trang 36 SGK Hình học 10 NC
Bài tập 12 trang 37 SGK Hình học 10 NC
Bài tập 13 trang 37 SGK Hình học 10 NC
Bài tập 14 trang 37 SGK Hình học 10 NC
Bài tập 15 trang 37 SGK Hình học 10 NC
Bài tập 16 trang 37 SGK Hình học 10 NC
Bài tập 17 trang 37 SGK Hình học 10 NC
Bài tập 18 trang 37 SGK Hình học 10 NC
Bài tập 19 trang 38 SGK Hình học 10 NC
Bài tập 20 trang 38 SGK Hình học 10 NC
Bài tập 21 trang 38 SGK Hình học 10 NC
-


Cho bốn điểm \(A, B, C, D\). Tìm các vec tơ: \(\overrightarrow v = \overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} \).
bởi Mai Thuy
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời -


Cho bốn điểm \(A, B, C, D\). Tìm các vec tơ: \(\overrightarrow u = \overrightarrow {AB} + \overrightarrow {DC} + \overrightarrow {BD} + \overrightarrow {CA} \).
bởi Nguyễn Phương Khanh
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời -


Trong hệ trục toạ độ đề các vuông góc Oxy cho hình vuông ABCD có A(0,2) C(4,0). Tìm toạ độ B, D.
bởi Nguyễn Ánh Dương
 20/02/2021
20/02/2021
Trong he truc toa do de cac vuong goc Oxy cho hinh vuong ABCD co A(0,2) C(4,0) Tim toa do B D
Theo dõi (0) 0 Trả lời -


Cho hình chữ nhật ABCD, đẳng thức nào sau đây là đúng ?
bởi Khánh An
 20/02/2021
20/02/2021
A. \(\overrightarrow {AB} + \overrightarrow {DB} = \overrightarrow {AD} \)
B. \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {BC} \)
C. \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {CA} \)
D. \(\;\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right|\)
Theo dõi (0) 1 Trả lời