Giải bài 1.60 tr 44 SBT Hình học 10
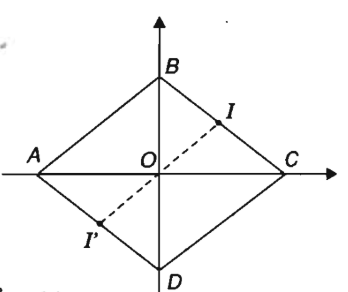
Cho hình thoi ABCD tâm O có AC = 8, BD = 6. Chọn hệ tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\) sao cho \(\overrightarrow i \) và \(\overrightarrow {OC}\) cùng hướng, \(\overrightarrow j\) và \(\overrightarrow {OB}\) cùng hướng.
a) Tìm tọa độ các đỉnh của hình thoi;
b) Tìm tọa độ trung điểm I của BC và trọng tâm của tam giác ABC;
c) Tìm tọa độ điểm đối xứng I′ của I qua tâm O. Chứng minh A, I′, D thẳng hàng;
d) Tìm tọa độ của vec tơ \(\overrightarrow {AC} ,\overrightarrow {BD} ,\overrightarrow {BC} \).
Hướng dẫn giải chi tiết
a) Do \(AC = 8 \Rightarrow OA = OC = 4\) nên A(-4;0), C(4;0)
Do \(DB = 6 \Rightarrow OB = OD = 3\) nên \(\left\{ \begin{array}{l}
{x_I} = \frac{{0 + 4}}{2} = 2\\
{y_I} = \frac{{3 + 0}}{2} = \frac{3}{2}
\end{array} \right.\) hay \(I\left( {2;\frac{3}{2}} \right)\)
Do G là trọng tâm tam giác ABC nên \(\left\{ \begin{array}{l}
{x_G} = \frac{{ - 4 + 0 + 4}}{3} = 0\\
{y_G} = \frac{{0 + 3 + 0}}{3} = 1
\end{array} \right.\) hay G(0;1).
c) Gọi I′ là điểm đối xứng với I qua O.
Khi đó O là trung điểm II′ hay \(\left\{ \begin{array}{l}
0 = \frac{{2 + {x_{I'}}}}{2}\\
0 = \frac{{\frac{3}{2} + {y_{I'}}}}{2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_{I'}} = - 2\\
{y_{I'}} = - \frac{3}{2}
\end{array} \right.\) hay \(I'\left( { - 2; - \frac{3}{2}} \right)\)
Ta có: \(\overrightarrow {AI'} = \left( {2; - \frac{3}{2}} \right),\overrightarrow {AD} = \left( {4; - 3} \right)\)
\(\overrightarrow {AD} \) nên ba điểm A, I′, D thẳng hàng.
d) Ta có:
\(\begin{array}{l}
\overrightarrow {AC} = \left( {4 - \left( { - 4} \right);0 - 0} \right) = \left( {8;0} \right)\\
\overrightarrow {BD} = \left( {0 - 0; - 3 - 3} \right) = \left( {0; - 6} \right)\\
\overrightarrow {BC} = \left( {4 - 0;0 - 3} \right) = \left( {4; - 3} \right)
\end{array}\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1.58 trang 44 SBT Hình học 10
Bài tập 1.59 trang 44 SBT Hình học 10
Bài tập 1.61 trang 44 SBT Hình học 10
Bài tập 1.62 trang 44 SBT Hình học 10
Bài tập 1.63 trang 44 SBT Hình học 10
Bài tập 1.64 trang 45 SBT Hình học 10
Bài tập 1.65 trang 45 SBT Hình học 10
Bài tập 1.66 trang 45 SBT Hình học 10
Bài tập 1.67 trang 45 SBT Hình học 10
Bài tập 1.68 trang 45 SBT Hình học 10
Bài tập 1.69 trang 45 SBT Hình học 10
Bài tập 1.70 trang 45 SBT Hình học 10
Bài tập 1.71 trang 46 SBT Hình học 10
Bài tập 1.72 trang 46 SBT Hình học 10
Bài tập 1.73 trang 46 SBT Hình học 10
Bài tập 1.74 trang 46 SBT Hình học 10
Bài tập 1.75 trang 46 SBT Hình học 10
Bài tập 1.76 trang 46 SBT Hình học 10
Bài tập 1.77 trang 46 SBT Hình học 10
Bài tập 1.78 trang 46 SBT Hình học 10
Bài tập 1.79 trang 47 SBT Hình học 10
Bài tập 1.80 trang 47 SBT Hình học 10
Bài tập 1.81 trang 47 SBT Hình học 10
Bài tập 1.82 trang 47 SBT Hình học 10
Bài tập 1.83 trang 47 SBT Hình học 10
Bài tập 1.84 trang 48 SBT Hình học 10
Bài tập 1.85 trang 47 SBT Hình học 10
Bài tập 1.86 trang 48 SBT Hình học 10
Bài tập 1.87 trang 48 SBT Hình học 10
Bài tập 1.88 trang 48 SBT Hình học 10
Bài tập 1.89 trang 49 SBT Hình học 10
Bài tập 1.90 trang 49 SBT Hình học 10
Bài tập 1.91 trang 49 SBT Hình học 10
Bài tập 1.92 trang 49 SBT Hình học 10
Bài tập 1.93 trang 49 SBT Hình học 10
Bài tập 1.95 trang 49 SBT Hình học 10
Bài tập 1.96 trang 49 SBT Hình học 10
Bài tập 1.97 trang 50 SBT Hình học 10
Bài tập 1.98 trang 50 SBT Hình học 10
Bài tập 1.99 trang 50 SBT Hình học 10
Bài tập 1.100 trang 50 SBT Hình học 10
Bài tập 1 trang 34 SGK Hình học 10 NC
Bài tập 2 trang 34 SGK Hình học 10 NC
Bài tập 3 trang 34 SGK Hình học 10 NC
Bài tập 4 trang 34 SGK Hình học 12 NC
Bài tập 5 trang 35 SGK Hình học 12 NC
Bài tập 6 trang 35 SGK Hình học 12 NC
Bài tập 7 trang 36 SGK Hình học 10 NC
Bài tập 8 trang 36 SGK Hình học10 NC
Bài tập 9 trang 36 SGK Hình học 10 NC
Bài tập 10 trang 36 SGK Hình học 10 NC
Bài tập 11 trang 36 SGK Hình học 10 NC
Bài tập 12 trang 37 SGK Hình học 10 NC
Bài tập 13 trang 37 SGK Hình học 10 NC
Bài tập 14 trang 37 SGK Hình học 10 NC
Bài tập 15 trang 37 SGK Hình học 10 NC
Bài tập 16 trang 37 SGK Hình học 10 NC
Bài tập 17 trang 37 SGK Hình học 10 NC
Bài tập 18 trang 37 SGK Hình học 10 NC
Bài tập 19 trang 38 SGK Hình học 10 NC
Bài tập 20 trang 38 SGK Hình học 10 NC
Bài tập 21 trang 38 SGK Hình học 10 NC
-


Tìm điểm M trên denta sao cho |vécto MA + véctơ MB + 3 véctơ MC | nhỏ nhất.
bởi Khánh Linh
 14/09/2020
14/09/2020
Bài 1. Cho tam giác ABC và đường đenta. Tìm điểm M trên denta sao cho |vécto MA + véctơ MB + 3 véctơ MC | nhỏ nhất.
Bài 2. Cho 2 điểm A,B và đường thẳng d. Tìm điểm M trên d sao cho | véctơ MA + 2 véctơ MB | nhỏ nhất.
Theo dõi (1) 0 Trả lời -


Tìm VTCP, VTPT, hệ số góc, PT tổng quát của đường thẳng \(\Delta :\left\{ \begin{array}{l} x = - 2 + 2t\\ y = 3 + 3t \end{array} \right.\)?
bởi Luận Đoàn
 09/06/2020
09/06/2020
Giúp em giải bài tập
Giúp em làm bài trắc nghiệm với ạ
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hình bình hành ABCD. Gọi I là trung điểm của CD, G là trọng tâm tam giác BCI . Đặt \(\overrightarrow a = \overrightarrow {AB} ,\overrightarrow b = \overrightarrow {AD} \) . Hãy tìm đẳng thức đúng trong các đẳng thức sau?
bởi Trịnh Lan Trinh
 30/05/2020
Theo dõi (0) 1 Trả lời
30/05/2020
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC biết \(AB = 3,BC = 4,AC = 6\) , I là tâm đường tròn nội tiếp tam giác ABC .Gọi x,y,z là các số thực dương thỏa mãn \(x.\overrightarrow {IA} + y.\overrightarrow {IB} + z.\overrightarrow {IC} = \overrightarrow 0 \).Tính \(P = \frac{x}{y} + \frac{y}{z} + \frac{z}{x}\)
bởi Mai Bảo Khánh
 31/05/2020
Theo dõi (0) 1 Trả lời
31/05/2020
Theo dõi (0) 1 Trả lời