Bài tập 4 trang 34 SGK Hình học 12 NC

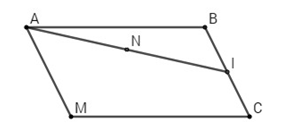
a) Ta có:

\(\begin{array}{l}
\overrightarrow {MA}  - \overrightarrow {MB}  + \overrightarrow {MC}  = \vec 0\\
 \Leftrightarrow \overrightarrow {BA}  + \overrightarrow {MC}  = \vec 0
\end{array}\)

⇔ \(\overrightarrow {CM}  = \overrightarrow {BA} \). 

Do đó ABCM là hình bình hành.

Gọi I là trung điểm của BC, ta có:

\(\overrightarrow {NB}  + \overrightarrow {NC}  = 2\overrightarrow {NI} \) 

Suy ra \(2\overrightarrow {NA}  + 2\overrightarrow {NI}  = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {NA}  + \overrightarrow {NI}  = \overrightarrow 0  \Rightarrow \) N là trung điểm của AI.

b) Từ câu a), ta biểu diễn \(\overrightarrow {AM} ,\overrightarrow {AN} \) qua \(\overrightarrow {AB} ,\overrightarrow {AC} \).

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {MA}  - \overrightarrow {MB}  + \overrightarrow {MC}  = \vec 0\\
 \Leftrightarrow  - \overrightarrow {AM}  - \left( {\overrightarrow {AB}  - \overrightarrow {AM} } \right) + \left( {\overrightarrow {AC}  - \overrightarrow {AM} } \right) = \vec 0
\end{array}\\
{ \Leftrightarrow \overrightarrow {AM}  =  - \overrightarrow {AB}  + \overrightarrow {AC} }\\
\begin{array}{l}
2\overrightarrow {NA}  + \overrightarrow {NB}  + \overrightarrow {NC}  = \vec 0\\
 \Leftrightarrow  - 2\overrightarrow {AN}  + \overrightarrow {AB}  - \overrightarrow {AN}  + \overrightarrow {AC}  - \overrightarrow {AN}  = \vec 0
\end{array}\\
\begin{array}{l}
 \Leftrightarrow 4\overrightarrow {AN}  = \overrightarrow {AB}  + \overrightarrow {AC} \\
 \Leftrightarrow \overrightarrow {AN}  = \frac{1}{4}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)
\end{array}\\
\begin{array}{l}
 \Rightarrow \overrightarrow {MN}  = \overrightarrow {AN}  - \overrightarrow {AM} \\
 = \frac{1}{4}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right) + \overrightarrow {AB}  - \overrightarrow {AC}  = \frac{5}{4}\overrightarrow {AB}  - \frac{3}{4}\overrightarrow {AC} 
\end{array}
\end{array}\)

Vậy \(p = \frac{5}{4};q =  - \frac{3}{4}\)

-- Mod Toán 10 HỌC247