Bài tập 6 trang 79 SGK Đại số 10

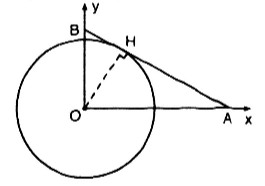
Gọi A(a; 0), B(0;b) (a,b > 0)

\(\begin{array}{l} \Rightarrow AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{a^2} + {b^2}} \\OA = \left| {\overrightarrow {OA} } \right| = a;OB = \left| {\overrightarrow {OB} } \right| = b\end{array}\)

Do AB tiếp xúc với đường tròn tâm O, bán kính R = 1,

Suy ra: diện tích \((\Delta OAB) = \frac{1}{2}AB.{h_0} = \frac{1}{2}AB.1 = \frac{1}{2}\sqrt {{a^2} + {b^2}} \)

Mặt khác: Diện tích \((\Delta OAB) = \frac{1}{2}OA.OB = \frac{1}{2}a.b\)

\( \Rightarrow \frac{1}{2}\sqrt {{a^2} + {b^2}}  = \frac{1}{2}ab \Leftrightarrow ab = \sqrt {{a^2} + {b^2}} \,\,(1)\)

Lại có theo bất đẳng thức cô–si:

\(\sqrt {{a^2} + {b^2}}  \ge \sqrt 2 .\sqrt {ab} \)

Nên từ (1) \( \Rightarrow ab \ge \sqrt 2 .\sqrt {ab}  \Leftrightarrow \sqrt {ab} (\sqrt {ab}  - \sqrt 2 ) \ge 0\)

\( \Leftrightarrow \sqrt {ab}  - \sqrt 2  \ge 0 \Leftrightarrow \sqrt {ab}  \ge \sqrt 2 \)

Do đó AB nhỏ nhất \(\Leftrightarrow \left\{ \begin{array}{l}\sqrt {ab}  = \sqrt 2 \\a = b\end{array} \right. \Leftrightarrow a = b = \sqrt 2 \)

Vậy AB nhỏ nhất khi \(A(\sqrt 2 ;0),B(0;\sqrt 2 )\)

-- Mod Toán 10 HỌC247